Stata'da tek yönlü anova nasıl gerçekleştirilir?

Üç veya daha fazla bağımsız grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için tek yönlü ANOVA kullanılır.

Bu tür testlere tek yönlü ANOVA denir çünkü bir yordayıcı değişkenin bir yanıt değişkeni üzerindeki etkisini analiz ederiz. Bunun yerine iki öngörücü değişkenin bir yanıt değişkeni üzerindeki etkisiyle ilgilenseydik, iki yönlü bir ANOVA gerçekleştirebilirdik.

Bu eğitimde Stata’da tek yönlü ANOVA’nın nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: Stata’da Tek Yönlü ANOVA

Bu örnekte tek yönlü ANOVA gerçekleştirmek için sistolik adı verilen yerleşik Stata veri kümesini kullanacağız. Bu veri seti 58 farklı birey için aşağıdaki üç değişkeni içermektedir:

• Kullanılan ilaç
• Hasta hastalığı
• Sistolik kan basıncında değişiklik

Kullanılan ilaç türünün sistolik kan basıncındaki değişiklik üzerinde önemli bir etkiye neden olup olmadığını belirlemek amacıyla tek yönlü bir ANOVA gerçekleştirmek için aşağıdaki adımları kullanacağız.

Adım 1: Verileri yükleyin.

Öncelikle komut kutusuna webuse sistolik yazıp Enter tuşuna basarak verileri yükleyin.

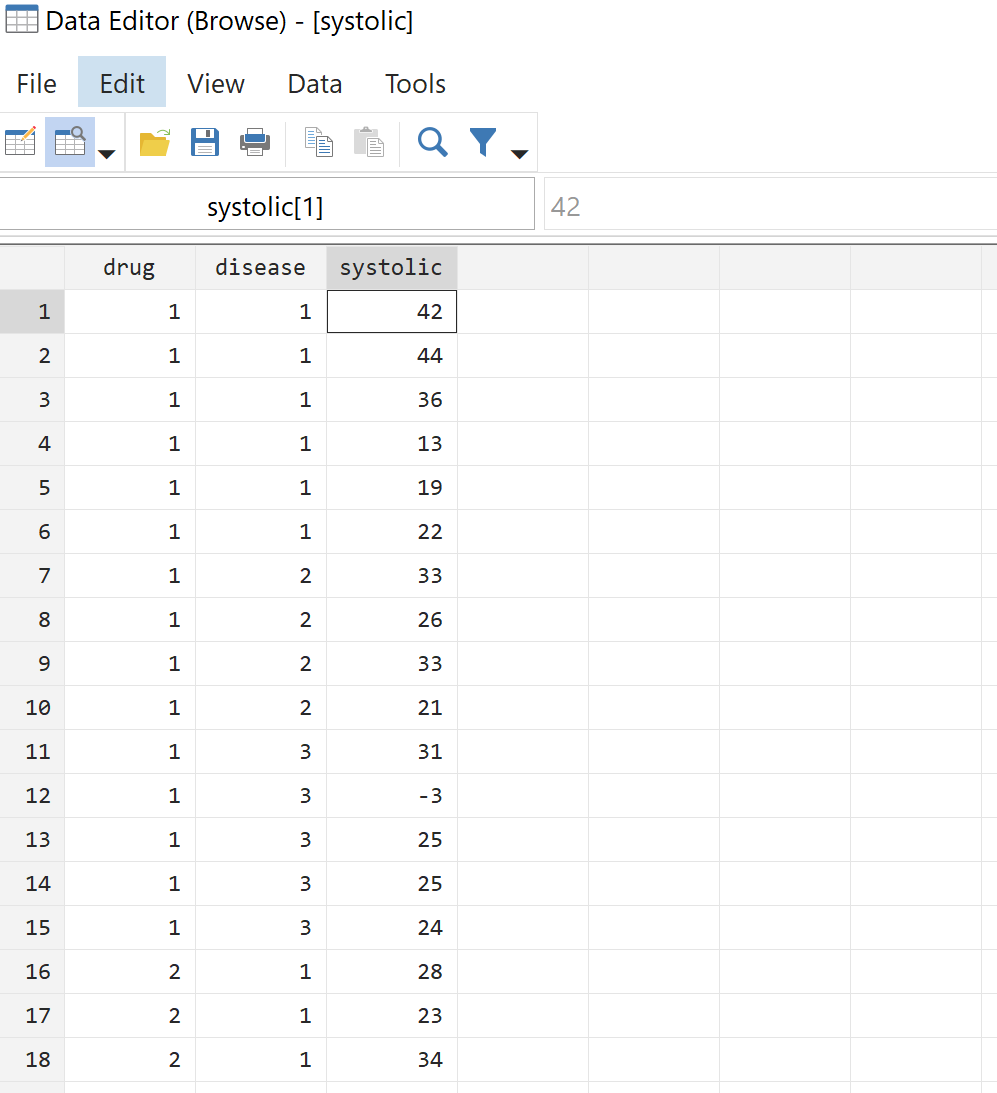
Adım 2: Ham verileri görüntüleyin.

Tek yönlü ANOVA yapmadan önce ham verilere bakalım. Üst menü çubuğundan Veri > Veri Düzenleyici > Veri Düzenleyici (Gözat) seçeneğine gidin. Bu bize 58 hastanın tamamı için gerçek verileri gösterecektir:

Adım 3: Verileri görselleştirin.

Daha sonra verileri görselleştirelim. Her ilaç kategorisi için sistolik kan basıncı değerlerinin dağılımını görüntülemek için kutu grafikleri oluşturacağız.

Üst menü çubuğundan Grafikler > Kutu grafiği seçeneğine gidin. Değişkenler altında Sistolik’i seçin:

Ardından, Gruplandırma değişkeni altındaki Kategoriler alt başlığında ilacı seçin:

Tamam’ı tıklayın. Dört kutu grafiğine sahip bir grafik otomatik olarak görüntülenecektir:

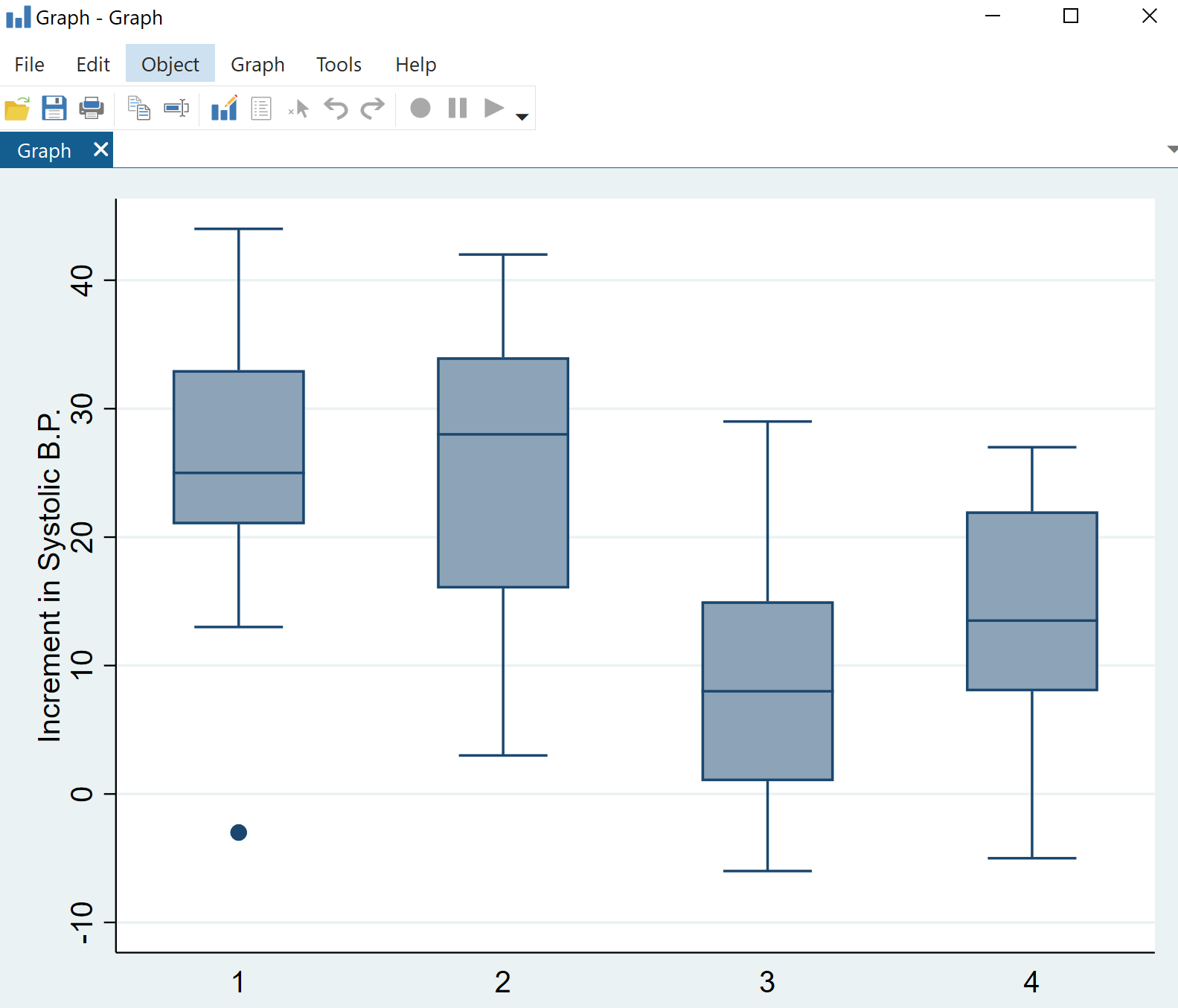
Sistolik kan basıncındaki değişikliklerin dağılımının ilaç kategorilerine göre değiştiğini hemen görebiliriz, ancak tek yönlü bir ANOVA bize bu farklılıkların istatistiksel olarak anlamlı olup olmadığını söyleyecektir.

Adım 4: Tek yönlü ANOVA gerçekleştirin.

Üst menü çubuğundan İstatistikler > Doğrusal ve İlgili Modeller > ANOVA/MANOVA > Tek Yönlü ANOVA seçeneğine gidin.

Yanıt Değişkeni altında Sistolik’i seçin. Faktör değişkeni altında ilacı seçin. Daha sonra, Özet Tablo Oluştur’un yanındaki kutuya tıklayın, böylece her grup için bazı temel tanımlayıcı istatistikleri görebiliriz. Daha sonra Tamam’ı tıklayın.

Aşağıdaki çıktı görüntülenecektir:

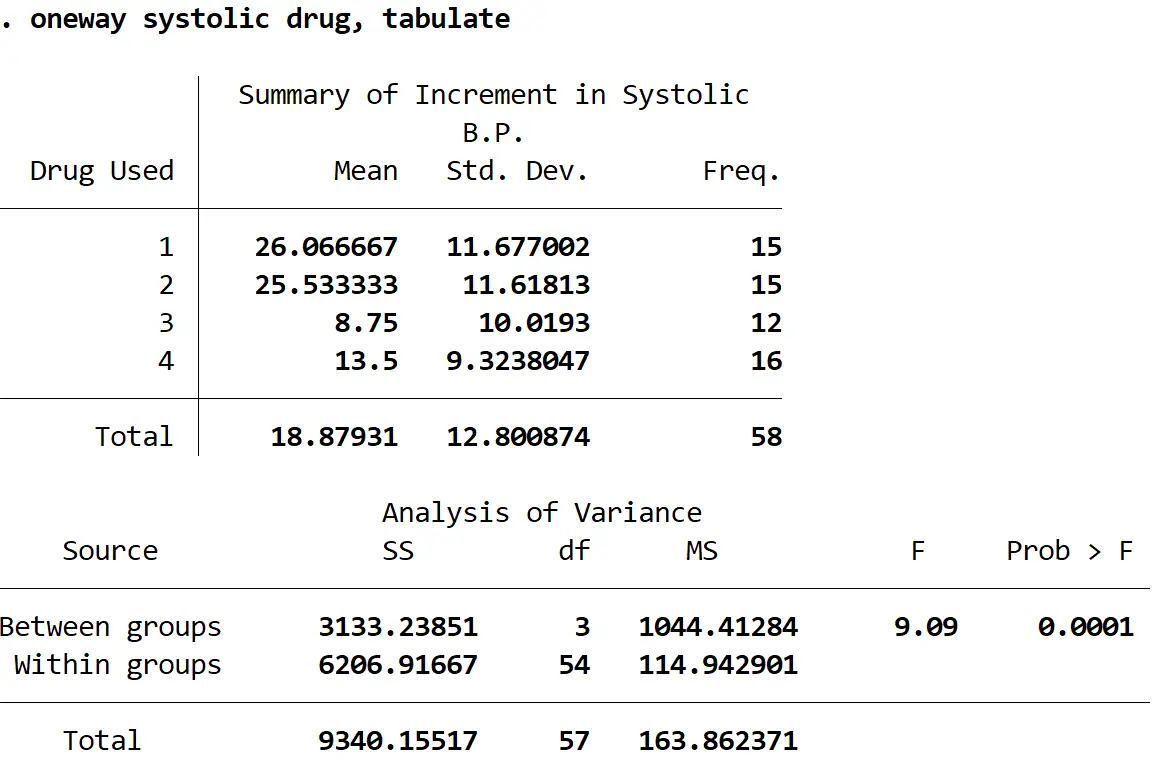
F istatistiği 9,09’dur ve buna karşılık gelen p değeri 0,0001’dir . P değeri alfa = 0,05’ten küçük olduğundan, her grup için sistolik kan basıncındaki ortalama değişimin eşit olduğu şeklindeki boş hipotezi reddedebiliriz.

Başka bir deyişle, en az iki ilaç grubu arasında sistolik kan basıncındaki ortalama değişim açısından istatistiksel olarak anlamlı bir fark vardır.

Adım 5: Çoklu karşılaştırma testleri çalıştırın.

Daha sonra hangi grup ortalamalarının birbirinden farklı olduğunu bulmak için birkaç karşılaştırma testi yapabiliriz.

Üst menü çubuğundan İstatistikler > Özetler, Tablolar ve Testler > Özet ve Tanımlayıcı İstatistikler > Ortalamaların İkili Karşılaştırmaları seçeneğine gidin .

Değişken için Sistolik yanıt değişkenini seçin. Over için açıklayıcı değişkeni seçin. Çoklu karşılaştırmalar için ayarlama için Tukey yöntemini seçin.

Ardından, Raporlama alt başlığı altında, Efekt tabloları’nın yanındaki düğmeye tıklayın ve Güven aralıkları ve p değerleri ile efekt tablosunu göster’in yanındaki kutuyu işaretleyin. Daha sonra Tamam’ı tıklayın.

Aşağıdaki sonuçlar görüntülenecektir:

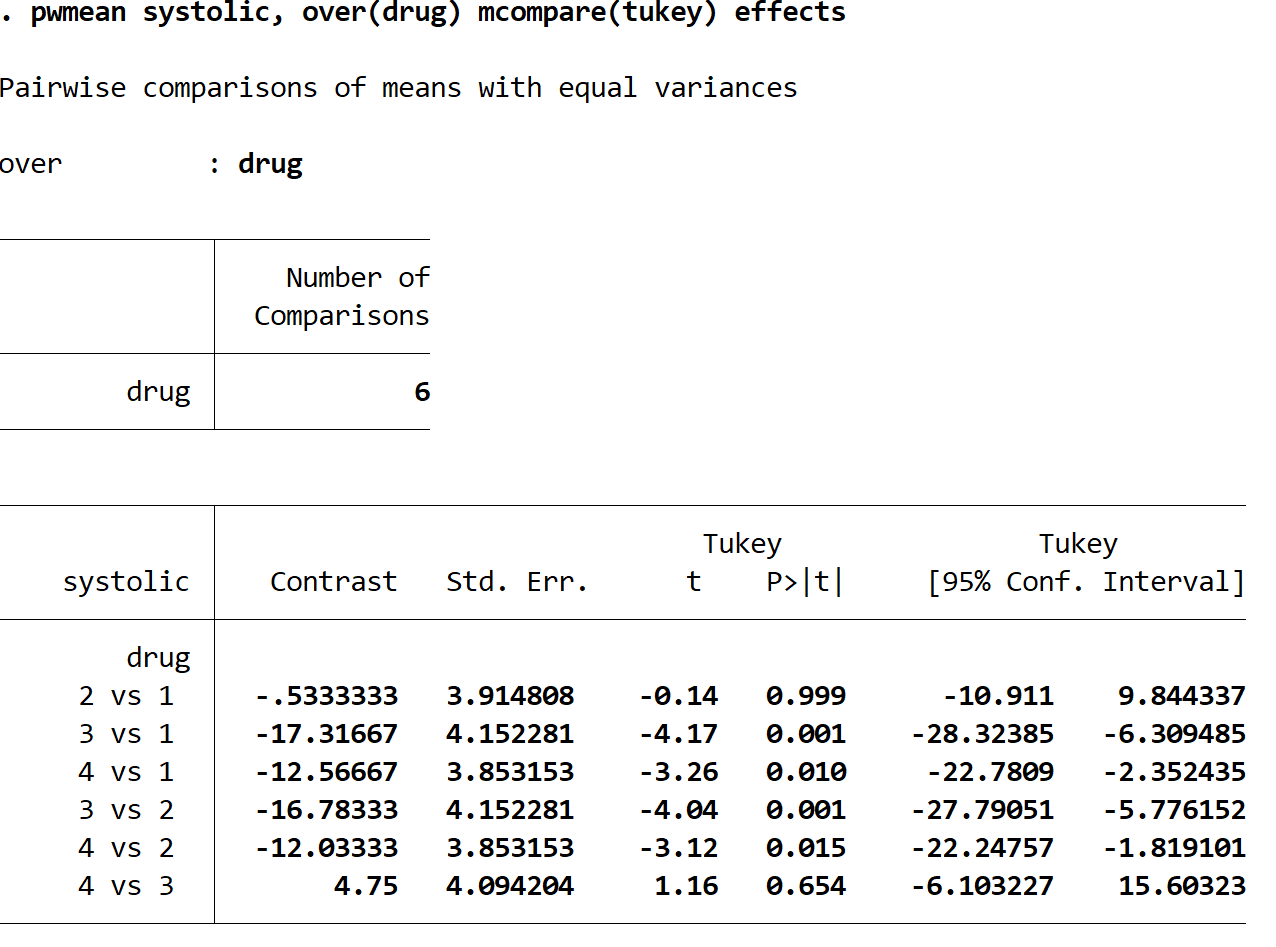
Her satır, iki spesifik ilaç grubu arasındaki karşılaştırmayı temsil eder. Örneğin, ilk satır ilaç grubu 2 ile ilaç grubu 1 arasındaki sistolik kan basıncındaki ortalama değişimi karşılaştırır. Bu karşılaştırmanın p değeri 0,999’dur ve bu son derece yüksektir ve 0,05’ten az değildir. Bu, ilaç grupları 1 ve 2 arasında istatistiksel olarak anlamlı bir fark olmadığı anlamına gelir.

Ancak aşağıdaki karşılaştırmalara ilişkin p değerlerinin tamamının 0,05’ten küçük olduğunu görebiliriz:

• tıp 3’e 1 | p-değeri = 0,001
• tıp 4’e 1 | p-değeri = 0,010
• tıp 3’e karşı 2 | p-değeri = 0,001
• tıp 4’e karşı 2 | p-değeri = 0,015

Bu, sistolik kan basıncındaki ortalama değişim farkının bu grupların her biri arasında istatistiksel olarak anlamlı olduğu anlamına gelir.

Adım 6: Sonuçları rapor edin.

Son olarak tek yönlü ANOVA analizimizin sonuçlarını raporlayacağız. İşte bunun nasıl yapılacağına dair bir örnek:

Dört farklı ilaç türünün sistolik kan basıncı üzerinde farklı etkileri olup olmadığını belirlemek için tek yönlü bir ANOVA yapıldı.

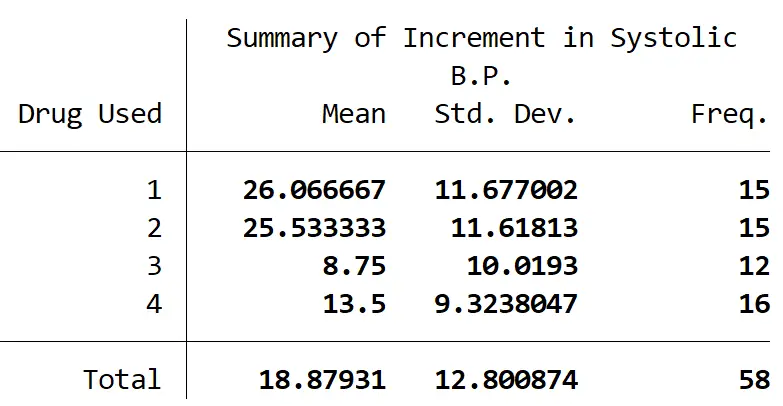
Aşağıdaki tablo, her gruptaki katılımcı sayısının yanı sıra her grup için sistolik kan basıncındaki ortalama değişiklik ve sistolik kan basıncının standart sapmasını özetlemektedir:

Tek yönlü ANOVA, en az iki grup arasında istatistiksel olarak anlamlı bir fark olduğunu ortaya çıkardı (F(3, 54) = 9,09, p = 0,001).

Çoklu karşılaştırmalara yönelik Tukey testi, sistolik kan basıncındaki değişimin ilaç 3 için ilaç 1’e göre istatistiksel olarak anlamlı derecede daha yüksek olduğunu (17,32 +/- 4,15, p = 0,001), ilaç 3 için ilaç 2’ye kıyasla (16,78 +/- 4,15, p = 0,001) olduğunu ortaya çıkardı. p = 0,001), ilaç 4 için ilaç 1 ile karşılaştırıldığında (12,57 +/- 3,85, p = 0,010) ve ilaç 4 için ilaç 2 ile karşılaştırıldığında (12,03 +/- 3,85, p = 0,015).

İlaç grupları 1 ve 2 (0,533 +/- 3,91, p = 0,999) veya ilaç grupları 3 ve 4 (4,75 +/- 4,09, p = 0,654) arasında istatistiksel olarak anlamlı bir fark yoktu.