Excel'de kruskal-wallis testi nasıl yapılır

Üç veya daha fazla bağımsız grubun medyanları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için Kruskal-Wallis testi kullanılır. Tek yönlü ANOVA’nın parametrik olmayan eşdeğeri olarak kabul edilir.

Bu eğitimde Excel’de Kruskal-Wallis testinin nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: Excel’de Kruskal-Wallis testi

Araştırmacılar, üç farklı gübrenin farklı bitki büyümesi düzeylerine yol açıp açmadığını bilmek istiyorlar. Rastgele 30 farklı bitki seçiyorlar ve bunları 10’arlı üç gruba ayırıyorlar ve her gruba farklı bir gübre uyguluyorlar. Bir ay sonra her bitkinin yüksekliğini ölçüyorlar.

Medyan büyümenin üç grupta da aynı olup olmadığını belirlemek amacıyla Kruskal-Wallis testi gerçekleştirmek için aşağıdaki adımları izleyin.

Adım 1: Verileri girin.

Her gruptaki 10 bitkinin her birinin toplam büyümesini (inç cinsinden) gösteren aşağıdaki verileri girin:

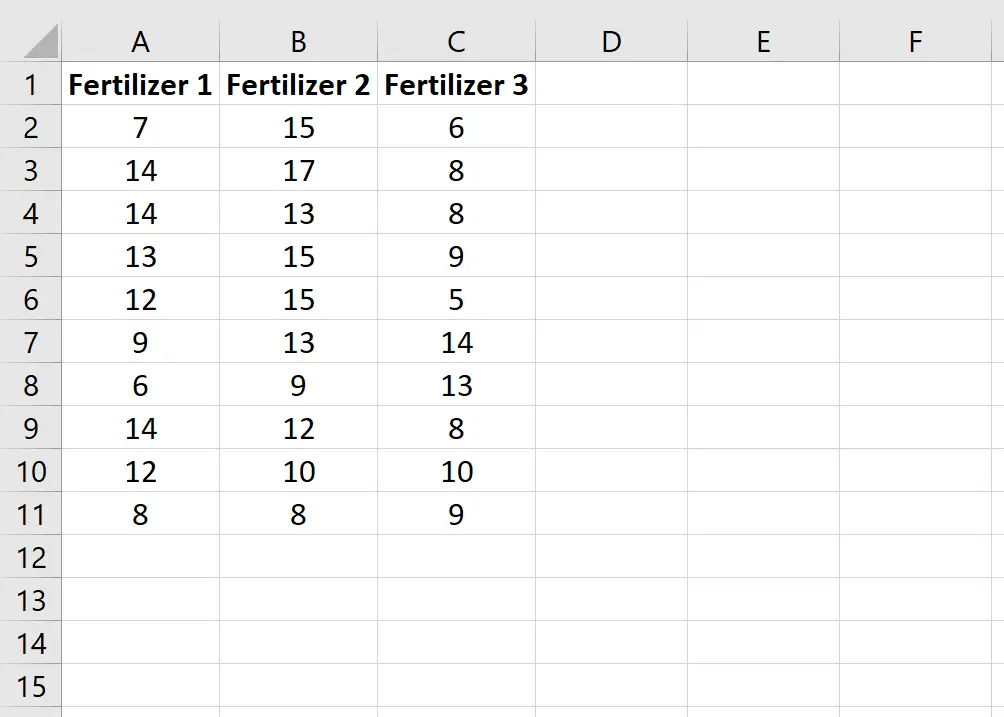
Adım 2: Verileri sınıflandırın.

Daha sonra, 30 bitki arasında her bitkinin büyümesine bir sıralama atamak için RANK.AVG() fonksiyonunu kullanacağız. Aşağıdaki formül, birinci gruptaki ilk bitkinin sıralamasının nasıl hesaplanacağını gösterir:

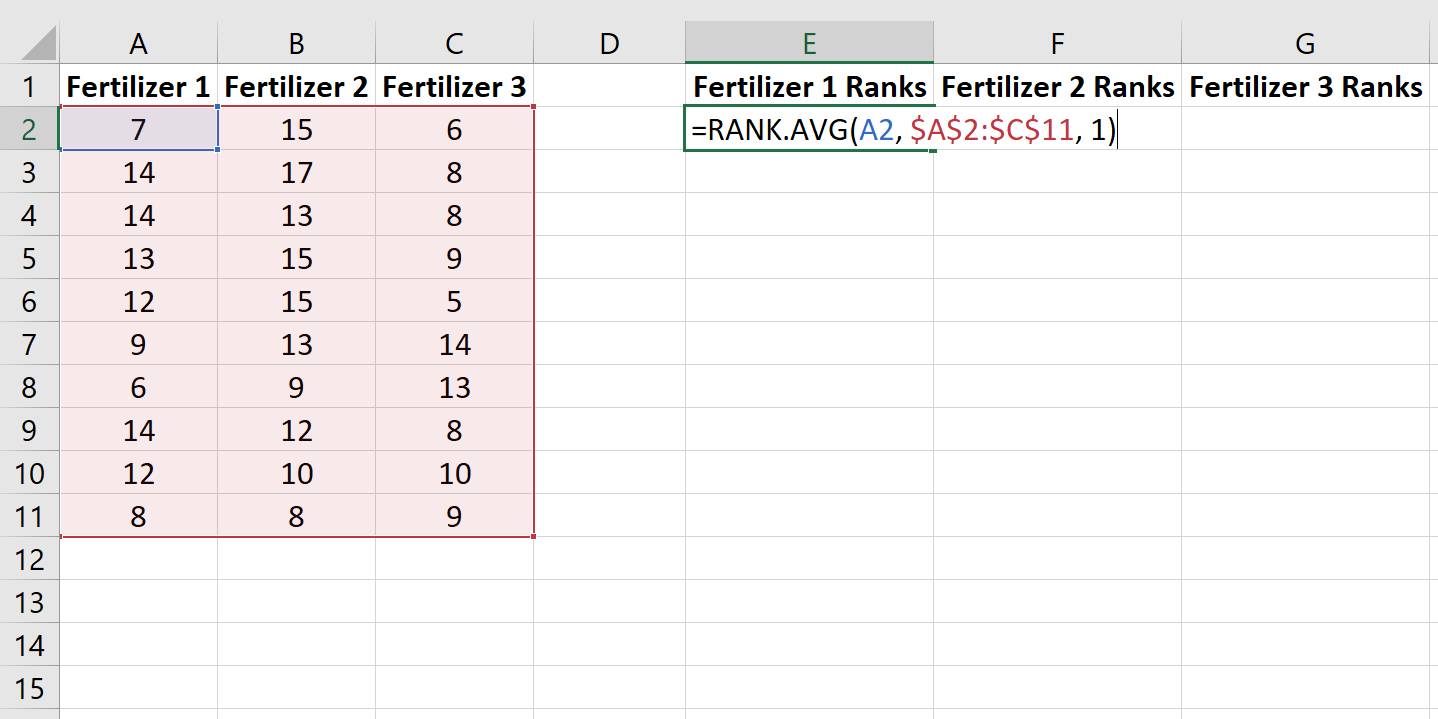
Bu formülü hücrelerin geri kalanına kopyalayın:

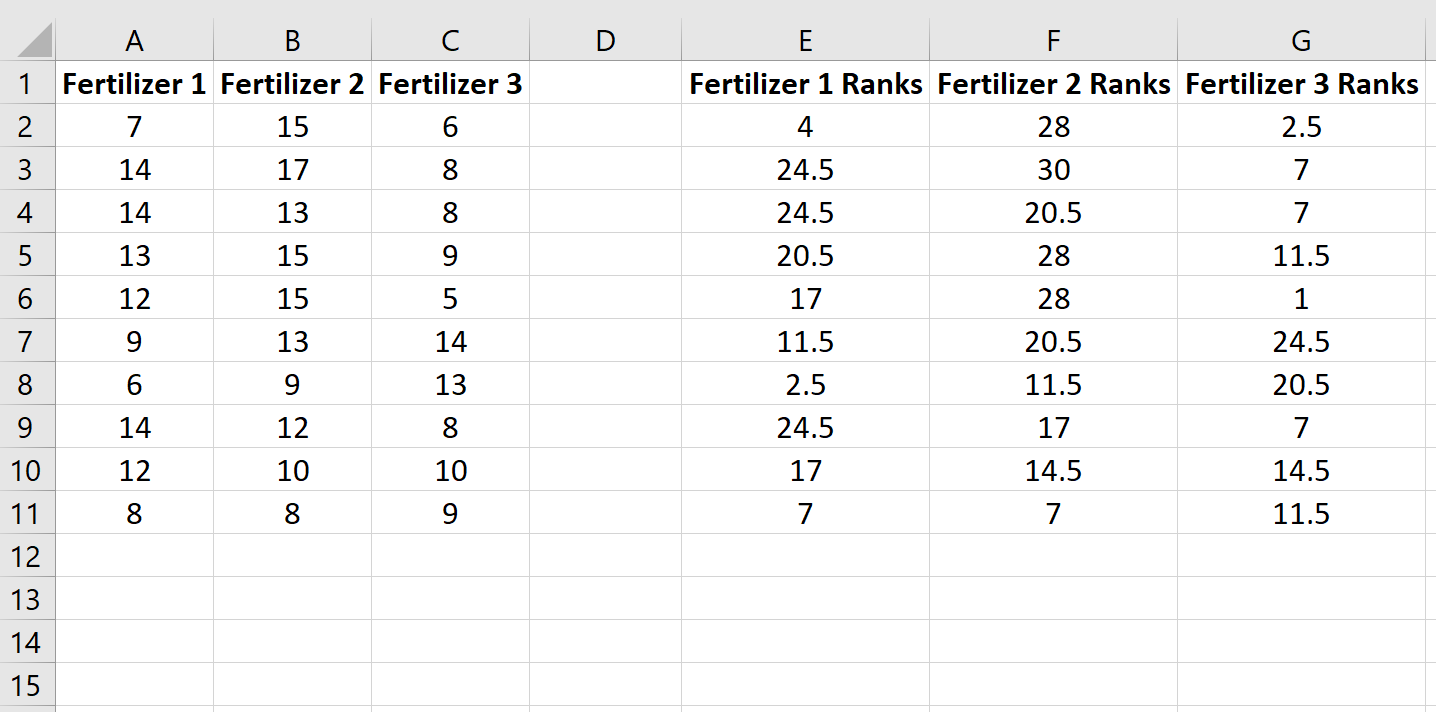
Daha sonra, her bir sütun için sıraların toplamını, örnek boyutu ve sıraların kare toplamının örnek boyutuna bölünmesiyle birlikte hesaplayın:

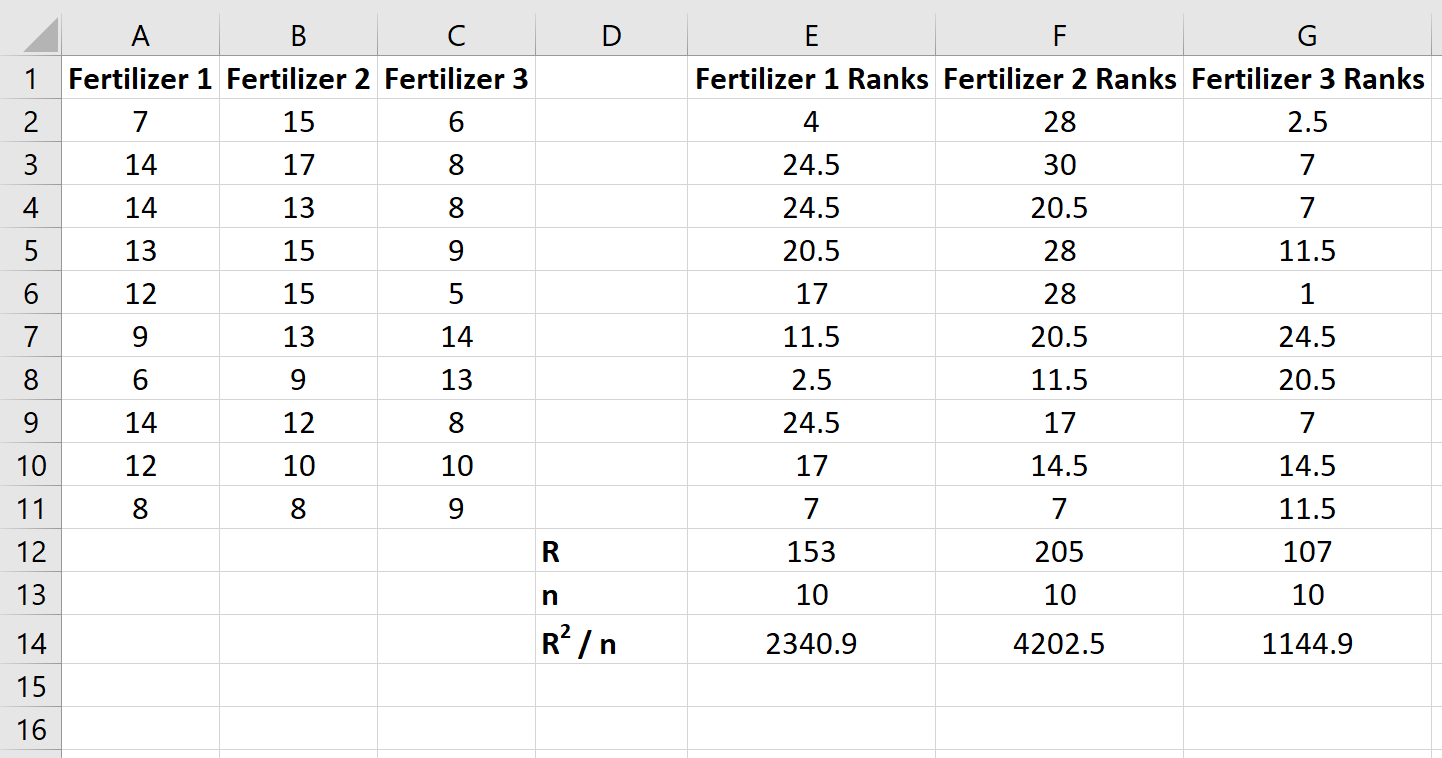
Adım 3: Test istatistiğini ve karşılık gelen p değerini hesaplayın.

Test istatistiği şu şekilde tanımlanır:

H = 12/(n(n+1)) * ΣR _j ² /n _j – 3(n+1)

Altın:

• n = toplam örneklem büyüklüğü
• R _j ² = ^j’inci grup için sıraların toplamı
• n _j = ^j’inci grubun örneklem büyüklüğü

Sıfır hipotezi altında H, k-1 serbestlik derecesine sahip bir Ki-kare dağılımını takip eder.

Aşağıdaki ekran görüntüsü test istatistiğini, H’yi ve karşılık gelen p değerini hesaplamak için kullanılan formülleri gösterir:

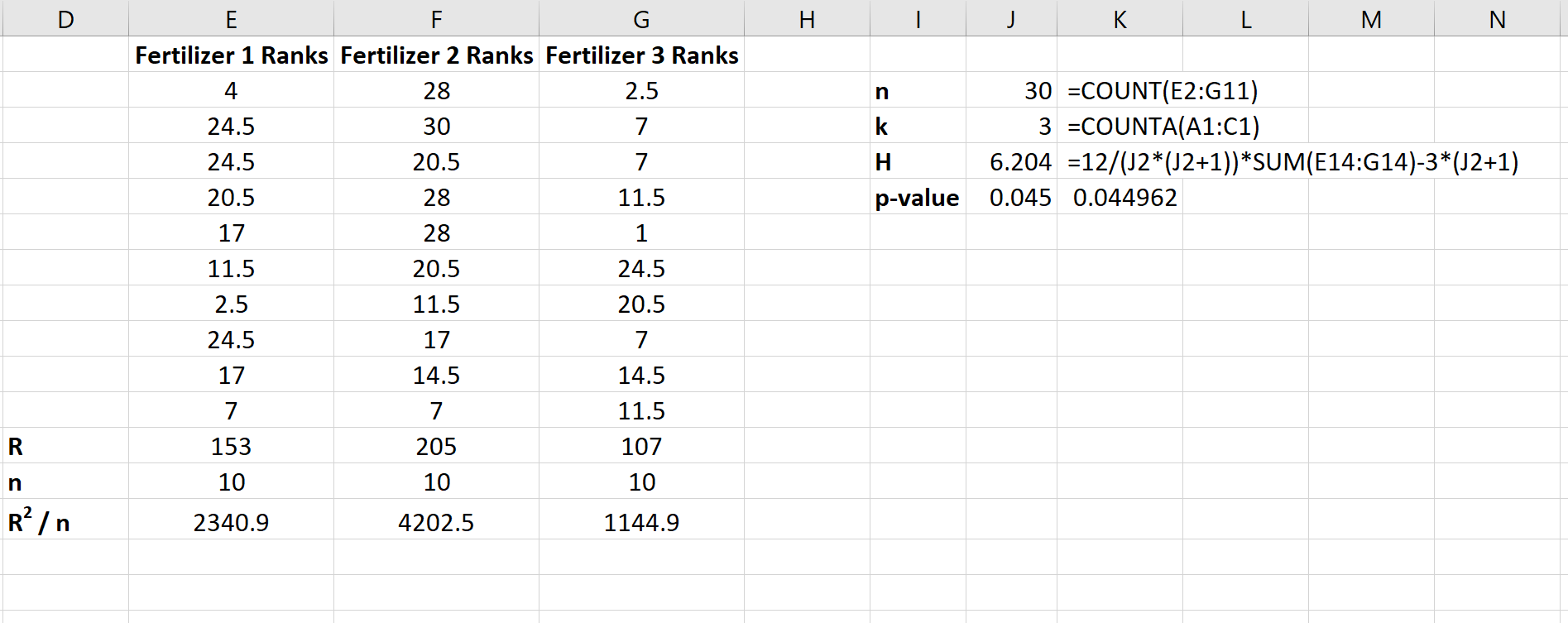
Test istatistiği H = 6,204’tür ve karşılık gelen p değeri p = 0,045’tir . Bu p değeri 0,05’ten küçük olduğundan, ortalama bitki büyümesinin her üç gübre için de aynı olduğu şeklindeki sıfır hipotezini reddedebiliriz. Kullanılan gübre türünün bitki büyümesinde istatistiksel olarak anlamlı farklılıklara neden olduğu sonucuna varmak için yeterli kanıtımız var.

Adım 4: Sonuçları rapor edin.

Son olarak Kruskal-Wallis testinin sonuçlarını bildirmek istiyoruz. İşte bunun nasıl yapılacağına dair bir örnek:

Ortalama bitki büyümesinin üç farklı bitki gübresi için aynı olup olmadığını belirlemek amacıyla Kruskal-Wallist testi yapıldı. Analizde toplam 30 bitki kullanıldı. Her gübre 10 farklı bitkiye uygulandı.

Test, üç gübre arasında ortalama bitki büyümesinin aynı olmadığını (H = 6,204, p = 0,045) ortaya çıkardı. Yani, iki veya daha fazla gübre arasında ortalama bitki büyümesi açısından istatistiksel olarak anlamlı bir fark vardı.