Çeyrekler arası aralık (veya çeyrekler arası aralık)

Bu makalede çeyrekler arası aralık olarak da bilinen çeyrekler arası aralığın ne olduğu açıklanmaktadır. Ayrıca çeyrekler arası aralığın nasıl hesaplandığını somut bir örnekle görebileceksiniz. Çeyrekler arası aralığın ne işe yaradığını ve aralıkla arasındaki farkı öğreneceksiniz. Ek olarak, çevrimiçi bir hesap makinesiyle herhangi bir veri kümesinin çeyrekler arası aralığını hesaplayabilirsiniz.

Çeyrekler arası (veya çeyrekler arası) aralık nedir?

Çeyrekler arası aralık olarak da adlandırılan çeyrekler arası aralık, üçüncü ve birinci çeyrekler arasındaki farkı gösteren istatistiksel dağılım ölçüsüdür. Bu nedenle, bir istatistiksel veri setinin çeyrekler arası aralığını hesaplamak için önce üçüncü ve birinci çeyrekleri bulmanız ve ardından bunları çıkarmanız gerekir.

Kısaca, çeyrekler arası aralık IQR kısaltmasıyla ifade edilir.

Çeyrekler arası aralığın en avantajlı özelliklerinden biri sağlam bir istatistik olması, yani aykırı değerlere karşı yüksek sağlamlığa sahip olmasıdır. Çeyrekler arası aralığın hesaplanmasında uç değerler dikkate alınmadığından, yeni aykırı değerlerin ortaya çıkması durumunda değeri çok az değişecektir.

Açıkçası, çeyrekler arası aralığın yanı sıra başka dağılım ölçümleri de vardır; en iyi bilinen ölçümler aralık, varyans, standart (veya standart) sapma, ortalama sapma ve varyasyon katsayısıdır.

Çeyrekler arası (veya çeyrekler arası) aralık nasıl hesaplanır?

İstatistikte, bir veri kümesinin çeyrekler arası aralığını (veya çeyrekler arası aralığı) hesaplamak için, önce veri kümesinin birinci ve üçüncü çeyreklerini bulmanız, ardından üçüncü çeyrekten birinci çeyreğin çıkarılmasını hesaplamanız gerekir.

Bu nedenle, çeyrekler arası aralığı veya çeyrekler arası aralığı hesaplamak için formül şöyledir:

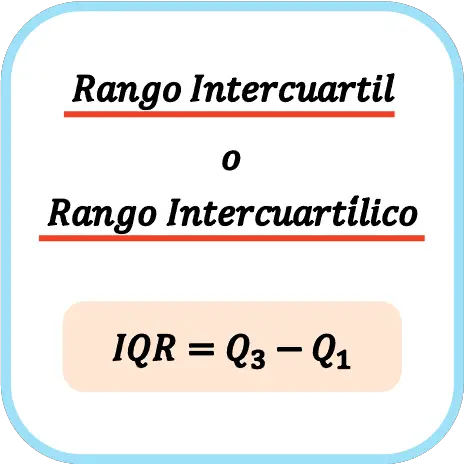
👉Herhangi bir veri seti için çeyrekler arası aralığı hesaplamak için aşağıdaki hesap makinesini kullanabilirsiniz.

Bu nedenle istatistiksel bir örneğin çeyreklerinin nasıl hesaplandığını bilmeniz önemlidir. Bu nedenle devam etmeden önce aşağıdaki yazıya göz atmanızı ve ardından açıklamalara devam etmenizi öneririm.

Çeyrekler arası (veya çeyrekler arası) aralık örneği

Çeyrekler arası aralığın (veya çeyrekler arası aralığın) tanımı ve formülü göz önüne alındığında, aşağıda çözülmüş bir alıştırma bulunmaktadır, böylece bu tür dağılım ölçüsünün tam olarak nasıl hesaplandığını görebilirsiniz.

• Bir şirkete yatırım yapmanın iyi bir fikir olup olmadığını istatistiksel olarak analiz etmek istiyoruz. Bunu yapmak için bu şirketin son 15 aydaki hisse senedi fiyatına ilişkin verileri topladık. Aşağıdaki tabloda gözlemlenen verileri en düşükten en yükseğe doğru sıralanmış olarak görebilirsiniz. Bu veri seti için çeyrekler arası aralığı hesaplayın.

Önceki bölümde gördüğümüz gibi, numunenin çeyrekler arası aralığını (veya çeyrekler arası aralığını) elde etmek için öncelikle birinci ve üçüncü çeyrekleri hesaplamamız gerekir.

İlk çeyrek, değerlerin ilk yarısının medyanıdır ve bu da hisse başına 8,95 Euro’ya karşılık gelir.

Öte yandan üçüncü çeyrek, değerlerin ikinci yarısının ara değeridir, dolayısıyla hisse başına 9,83 €’dur.

Yani çeyrekler arası aralığı bulmak için formülü uygulayın ve üçüncü çeyrekten birinci çeyrekten çıkarın.

Çeyrekler Arası (veya Çeyrekler Arası) Aralık Hesaplayıcı

Çeyrekler arası aralığı veya çeyrekler arası aralığı hesaplamak için aşağıdaki hesap makinesine bir istatistiksel veri seti girin. Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.

Çeyrekler Arası Aralık ve Aralık Arasındaki Fark

İstatistikte çeyrekler arası aralık (veya çeyrekler arası aralık) ile aralık arasındaki fark, hesaplamayı gerçekleştirmek için alınan değerlerdir. Çeyrekler arası aralık üçüncü ve birinci çeyrekler arasındaki farktır, aralık ise numunenin uç değerleri arasındaki farktır.

Böylece, çeyrekler arası aralık, merkezi verileri kullanarak bir numunenin dağılımını ölçerken, aralık, uç verileri kullanarak numunenin dağılımını ölçer.

Bu nedenle, istatistiksel aralık aykırı değerlerden çok daha fazla etkilenir çünkü bunlar genellikle veri kümesinin minimum veya maksimumunu temsil eder. Bu nedenle, çeyrekler arası aralığın aralıktaki avantajlarından biri, daha fazla sağlamlığa sahip olmasıdır.

Çeyrekler arası (veya çeyrekler arası) aralık ne için kullanılır?

Öncelikle çeyrekler arası aralık (veya çeyrekler arası aralık), bir veri kümesinin dağılımını ölçmek için kullanılır . Tam olarak Bir numunenin dağılımını analiz etmek daha fazla istatistiksel önlem hesaplamayı gerektirse de çeyrekler arası aralık, numunenin en azından merkezi değerlere ne kadar dağıldığına dair bir fikir sağlar.

Bu nedenle çeyrekler arası aralığın yorumlanması nispeten basittir. Çeyrekler arası aralığın değeri ne kadar yüksek olursa, ortadaki veriler örneklemde o kadar dağınık olur ve çeyrekler arası aralık ne kadar küçük olursa ortadaki veriler birbirine o kadar yakın olur.

Ek olarak çeyrekler arası aralık, borsadaki hisse senedi fiyat davranışını analiz etmek için yaygın olarak kullanılan bir diyagram olan kutu ve bıyık grafiği oluşturmak için de kullanışlıdır.