Ti-84 hesap makinesinde binom olasılıkları nasıl hesaplanır?

Binom dağılımı tüm istatistiklerde en sık kullanılan dağılımlardan biridir. Bu eğitimde, binom olasılıklarını bulmak için TI-84 hesap makinesinde aşağıdaki işlevlerin nasıl kullanılacağı açıklanmaktadır:

binompdf(n, p, x), binom pdf ile ilişkili olasılığı döndürür.

binomcdf(n, p, x), binom cdf ile ilişkili kümülatif olasılığı döndürür.

Altın:

• n = deneme sayısı
• p = belirli bir denemede başarı olasılığı
• x = toplam başarı sayısı

Bu iki fonksiyona TI-84 hesap makinesinde 2nd tuşuna ve ardından vars tuşuna basılarak erişilebilir. Bu sizi daha sonra binompdf() ve binomcdf() kullanabileceğiniz bir DISTR ekranına götürecektir:

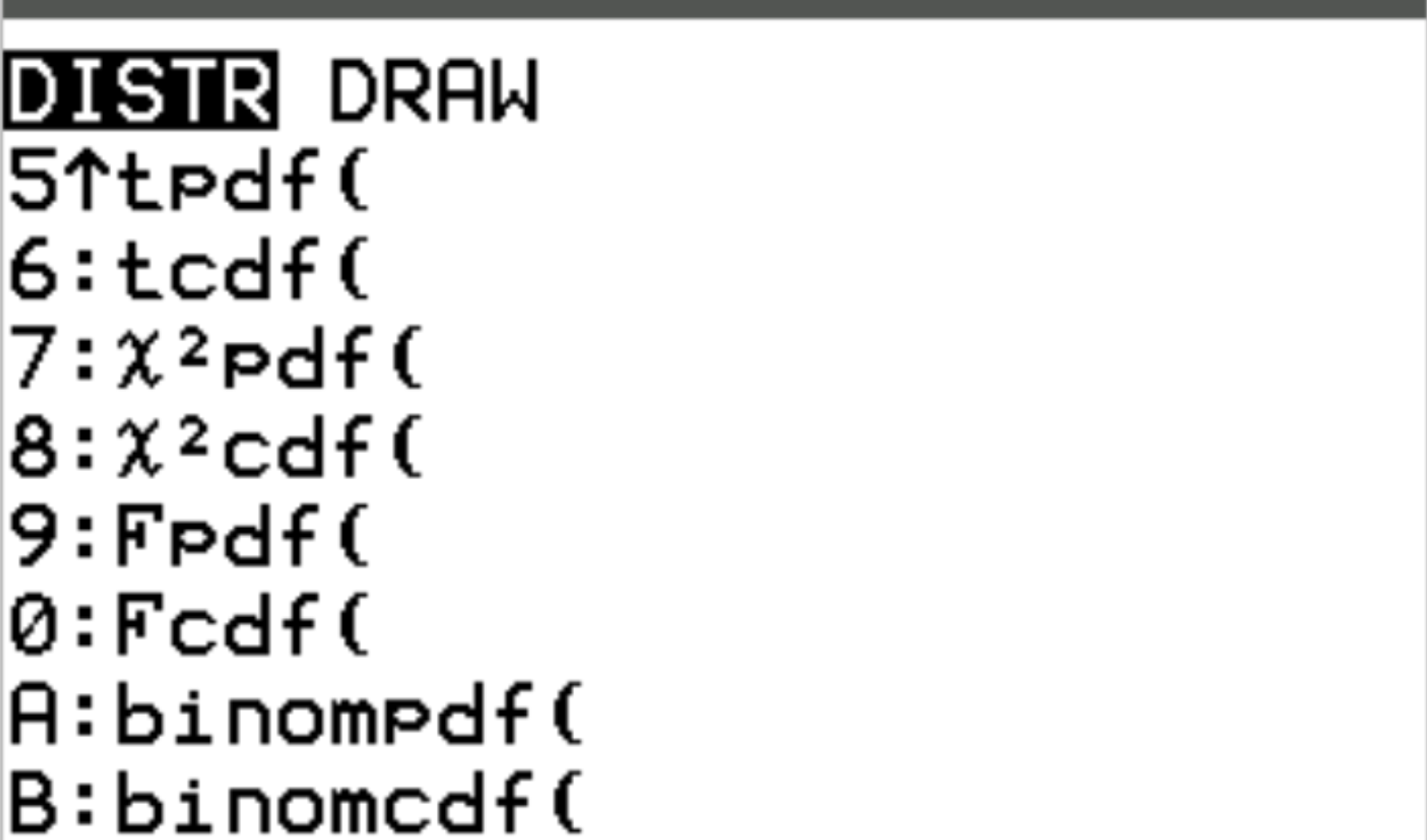
Aşağıdaki örnekler, farklı soruları yanıtlamak için bu işlevlerin nasıl kullanılacağını göstermektedir.

Örnek 1: Tam x başarının binom olasılığı

Soru: Nathan serbest atış denemelerinin %60’ını yapıyor. Eğer 12 serbest atış yaparsa tam olarak 10 atış yapma olasılığı nedir?

Cevap: binompdf(n, p, x) fonksiyonunu kullanın:

binompdf(12, .60, 10) = 0,0639

Örnek 2: x’ten küçük başarının binom olasılığı

Soru: Nathan serbest atış denemelerinin %60’ını yapıyor. Eğer 12 serbest atış yaparsa 10’dan az atış yapma olasılığı nedir?

Cevap: Binomcdf(n, p, x-1) fonksiyonunu kullanın:

binomcdf(12, .60, 9) = 0,9166

Örnek 3: en fazla x başarının binom olasılığı

Soru: Nathan serbest atış denemelerinin %60’ını yapıyor. 12 serbest atış yaparsa en fazla 10 atış yapma olasılığı nedir?

Cevap: Binomcdf(n, p, x) fonksiyonunu kullanın:

binomcdf(12, .60, 10) = 0,9804

Örnek 4: X’ten büyük başarıların binom olasılığı

Soru: Nathan serbest atış denemelerinin %60’ını yapıyor. Eğer 12 serbest atış yaparsa 10’dan fazla atış yapma olasılığı nedir?

Cevap: Fonksiyon 1’i kullanın – binomcdf(n, p, x) :

1 – binomcdf(12, .60, 10) = 0,0196

Örnek 5: En az x başarının binom olasılığı

Soru: Nathan serbest atış denemelerinin %60’ını yapıyor. Eğer 12 serbest atış yaparsa 10’dan fazla atış yapma olasılığı nedir?

Cevap: Fonksiyon 1’i kullanın – binomcdf(n, p, x-1) :

1 – binomcdf(12, .60, 9) = 0,0834