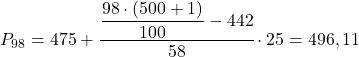Yüzdelikler (istatistikler)

İle Dr.benjamin anderson Ağustos 5, 2023 İstatistik 0 Yorum

Bu makalede yüzdelik dilimin ne olduğu ve nasıl hesaplandığı açıklanmaktadır. Çözülmüş yüzdelikler alıştırmaları bulacaksınız ve ayrıca çevrimiçi bir hesap makinesiyle veri örneğinizin herhangi bir yüzdelik dilimini hesaplayabileceksiniz.

Yüzdelikler nedir?

İstatistikte yüzdelikler, sıralı bir veri kümesini yüz eşit parçaya bölen değerlerdir. Yani yüzdelik dilim, veri kümesinin belirli bir yüzdesinin altına düştüğü değeri belirtir.

Örneğin 35. yüzdelik değer, gözlemlenen verilerin %35’inden yüksek, ancak verilerin geri kalanından daha düşüktür.

Yüzdelikler büyük harf P ve yüzdelik endeksi ile temsil edilir; yani 1. yüzdelik dilim P ₁ , 40. yüzdelik dilim P ₄₀ , 79. yüzdelik dilim P ₇₉ vb.

👉Herhangi bir veri setinin yüzdelik dilimlerini hesaplamak için aşağıdaki hesap makinesini kullanabilirsiniz.

Benzer şekilde yüzdelikler, çeyrekler, beşte birlikler ve ondalık dilimlerle birlikte merkezi olmayan konumun bir ölçüsüdür. Bu nicelik türlerinin her birinin anlamını web sitemizden kontrol edebilirsiniz.

Bebeğin doğru büyüyüp büyüyüp büyümediğini belirlemeye yardımcı olan kayıtlı değerlerin bulunduğu büyüme tabloları olduğundan, yüzdelik teriminin bir bebeğin kilosunu ve boyunu diğer bebeklerin standart değerleriyle karşılaştırmak için de kullanıldığı unutulmamalıdır. . .

Yüzdelikler nasıl hesaplanır

Bir istatistiksel veri serisinin yüzdelik diliminin konumunu hesaplamak için, yüzdelik sayıyı toplam veri noktası sayısının toplamı artı bir ile çarpmanız ve sonucu yüze bölmeniz gerekir.

Bu nedenle yüzdelik formül şu şekildedir:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

Lütfen unutmayın: Bu formül bize yüzdelik dilimin konumunu belirtir, ancak değerini vermez. Yüzdelik dilim, formülün elde ettiği konumda bulunan veriler olacaktır.

Ancak bazen bu formülün sonucu bize ondalık sayı verir, bu nedenle sonucun ondalık sayı olup olmadığına bağlı olarak iki durumu ayırmamız gerekir:

Formülün sonucu ondalık kısmı olmayan bir sayı ise yüzdelik dilim yukarıdaki formülün sağladığı konumdaki verilere karşılık gelir.
Formül sonucu ondalık kısmı olan bir sayıysa , tam yüzdelik değer aşağıdaki formül kullanılarak hesaplanır:

$P=x_i+d\cdot (x_{i+1}-x_i)$

Burada x _i ve x _i+1, birinci formülle elde edilen sayının aralarında bulunduğu konumların sayılarıdır ve d , birinci formülle elde edilen sayının ondalık kısmıdır.

Artık istatistiksel bir örneklemin veya popülasyonun yüzdelik dilimlerini bulmanın, yöntem birçok adım içerdiğinden karmaşık olduğunu düşünebilirsiniz, ancak aslında kolaydır. Aşağıdaki iki somut örneği okuyun eminim çok daha iyi anlayacaksınız.

Not : Bilimsel topluluk yüzdelik dilimlerin nasıl hesaplanacağı konusunda henüz tam bir fikir birliğine varmamıştır, dolayısıyla bunu biraz farklı açıklayan bir istatistik kitabı bulabilirsiniz.

Yüzdelik Hesaplama Örnekleri

Yukarıda bir numunenin yüzdelik değerlerinin nasıl bulunacağı açıklamasında gördüğünüz gibi, ilk formülün sonucunun ondalık olup olmamasına göre hesaplama değişmektedir. Bu nedenle aşağıda her durum için bir tane olmak üzere iki çözülmüş örnek bulacaksınız.

örnek 1

Aşağıdaki tabloda gösterilen verilerden 1., 43. ve 89. yüzdelikleri hesaplayın.

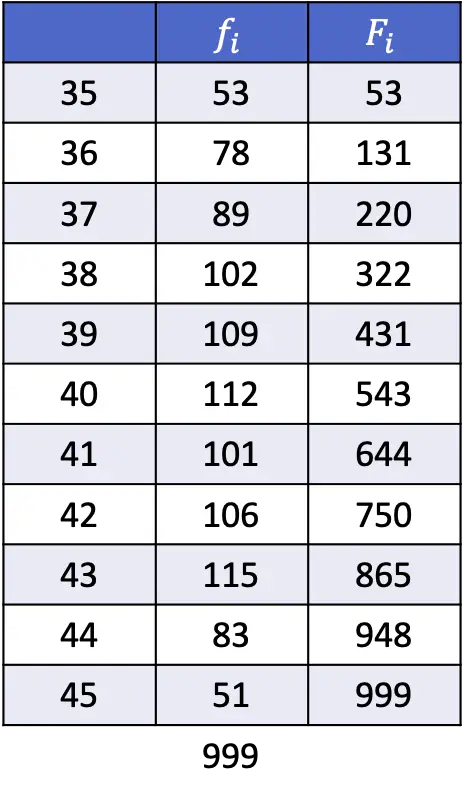
Önceki bölümde açıklandığı gibi yüzdelik dilimin konumunu bulma formülü şöyledir:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

Bu durumda, bu alıştırmanın örneklem büyüklüğü 999 istatistiksel veridir, dolayısıyla ilk yüzdelik dilimin konumunu hesaplamak için n yerine 999 ve k yerine 1 koymamız gerekir:

$\cfrac{1\cdot (999+1)}{100}=10\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_1=35$

Yani 1. yüzdelik dilim, kümülatif mutlak frekansı 10’dan hemen büyük olan olacaktır; kümülatif mutlak frekansı 53 olduğundan bu durumda bu 35’tir.

43. yüzdeliği belirlemek için aynı formülü kullanmanız gerekir, ancak açıkçası bu sefer k’yi 43 ile değiştireceğiz.

$\cfrac{43\cdot (999+1)}{100}=430\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_{43}=39$

430’un hemen üzerindeki mutlak kümülatif frekans, veri 39’un 431’idir, dolayısıyla 43’üncü yüzdelik dilim 39’a eşittir.

Son olarak 89. yüzdeliği elde etmek için aynı formülü uyguluyoruz:

$\cfrac{89\cdot (999+1)}{100}=890\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_{89}=44$

44 değerinin kümülatif mutlak frekansı 948’dir ve bu da 890’dan hemen büyüktür. Dolayısıyla 89. yüzdelik dilim 44’tür.

Örnek 2

Aşağıdaki veri serilerinin 35. ve 67. yüzdelik dilimlerini bulun:

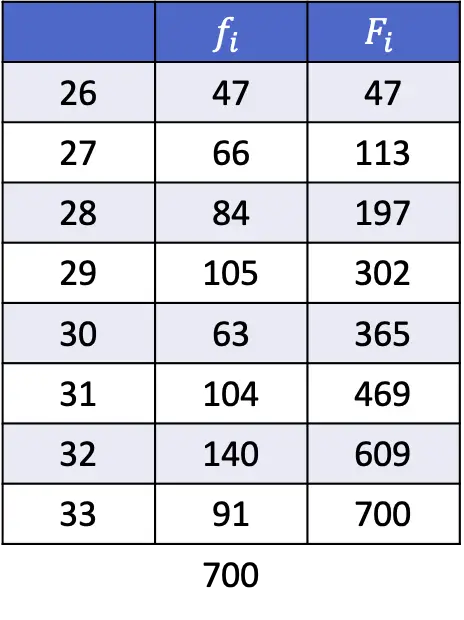
Bu alıştırmada daha fazla hesaplama yapmak zorunda kalsak bile prensip hala aynıdır: Yüzdelik konumu aşağıdaki ifadeyle hesaplamalıyız.

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,\ldots ,97,98,99$

Böylece, 35. yüzdeliği hesaplamak için k’yi 35 ile ve n’yi toplam veri sayısıyla, yani 700 ile değiştiririz:

$\cfrac{35\cdot (700+1)}{100}=245,35$

Ancak bu sefer formülden ondalık bir sayı elde ettik, dolayısıyla tam yüzdelik değeri hesaplamak için aşağıdaki cebirsel ifadeyi uygulamamız gerekiyor:

$P=x_i+d\cdot (x_{i+1}-x_i)$

İlk formülde verilen sayı 245,35’tir, yani 35’inci yüzdelik dilim 245 ile 246 konumları arasındadır ve bu da sırasıyla 29 ve 29 değerlerine karşılık gelir. Dolayısıyla x _i 29, x _i+1 29 ve d elde edilen sayının ondalık kısmına yani 0,35’e eşittir.

$P_{35}=29+0,35\cdot (29-29)=29$

67. yüzdeliği bulmak için aynı yöntemi kullanmamız gerekiyor. İlk önce yüzdelik konumunu hesaplıyoruz:

$\cfrac{67\cdot (700+1)}{100}=469,67$

Ortaya çıkan 469,67 sayısı yüzdelik dilimin 469 ile 470 konumları arasında olacağını, değerlerinin ise 31 ve 32 olduğunu belirtir. Bu nedenle tam yüzdelik değeri bulmak için işlemde ikinci formülü kullanırız:

$P_{67}=31+0,67\cdot (32-31)=31,67$

yüzdelik hesaplayıcı

Aşağıdaki hesap makinesine bir istatistiksel veri seti ve hesaplamak istediğiniz yüzdelik sayıyı girin. Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.

Gruplandırılmış verilerdeki yüzdelikler

Veriler gruplara ayrıldığında yüzdelik dilimleri hesaplamak için öncelikle aşağıdaki formülü kullanarak yüzdelik dilimin düştüğü grubu veya sınıfı bulmamız gerekir:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

Dolayısıyla yüzdelik dilim, mutlak frekansı önceki ifadede elde edilen sayıdan hemen büyük olan aralıkta olacaktır.

Yüzdelik dilimin ait olduğu aralığı zaten bildiğimizde, yüzdelik dilimin tam değerini bulmak için aşağıdaki formülü uygulamamız gerekir:

$P_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{100}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3,\ldots ,97,98,99$

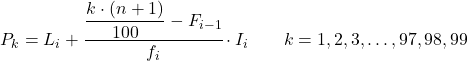
Altın:

L _i yüzdelik dilimin yer aldığı aralığın alt sınırıdır.
n , toplam gözlem sayısıdır.
F _i-1 önceki aralığın kümülatif mutlak frekansıdır.
f _i yüzdelik dilimin bulunduğu aralığın mutlak frekansıdır.
I _i yüzdelik aralığının genişliğidir.

Aşağıda, veriler aralıklarla ifade edildiğinde yüzdelik değerlerin nasıl elde edileceğine ilişkin adım adım bir alıştırma bulunmaktadır. Spesifik olarak 29., 52. ve 98. yüzdelikler hesaplanır.

Bu örnekteki veriler aralıklar halinde gruplandırılmıştır, dolayısıyla yüzdelik dilimleri belirlemek için iki adım uygulamamız gerekir: önce yüzdelik dilimin düştüğü aralığı bulmamız, ardından yüzdelik dilimin tam değerini hesaplamak için formülü uygulamamız gerekir. yüzdelik.

Böylece 29. yüzdelik dilimin konumunu aşağıdaki ifadeyle buluyoruz:

$\cfrac{k\cdot (n+1)}{100}$

$\cfrac{29\cdot (500+1)}{100} =145,29 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [350,375)$

Yüzdelik aralık, kümülatif mutlak frekansı 145,29’dan hemen büyük olan aralık olacaktır; bu durumda, kümülatif mutlak frekansı 175 olan aralık [350,375) olacaktır. Yüzdelik aralığını bildiğimizde, onun hesaplamak için aşağıdaki formülü uygularız. Kesin değer:

$P_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{100}-F_{i-1}}{f_i}\cdot I_i$

$P_{29}=350+\cfrac{\displaystyle\frac{29\cdot (500+1)}{100}-131}{44}\cdot 25=358,12$

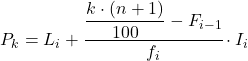
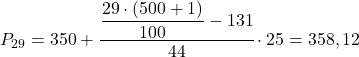
Şimdi 52. yüzdeliği hesaplamak için aynı işlemi tekrarlıyoruz. İlk önce aralığını hesaplıyoruz:

$\cfrac{52\cdot (500+1)}{100} =260,52 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [400,425)$

Kümülatif mutlak frekansı (298) 260,52’nin hemen üzerinde olduğundan 52’nci yüzdelik aralık [400,425’tir. Bu nedenle yüzdelik dilimin tam değeri şu şekilde olacaktır:

$P_{52}=400+\cfrac{\displaystyle\frac{52\cdot (500+1)}{100}-234}{64}\cdot 25=410,36$

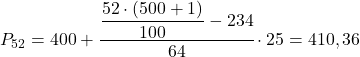
Son olarak 98. yüzdelik dilimi bulacağız. Her zaman olduğu gibi, önce bulunduğu aralığı hesaplıyoruz:

$\cfrac{98\cdot (500+1)}{100} =490,98 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [475,500)$

Yüzdelik dilimin bulunduğu aralığı bildiğimizde, tam değerini aşağıdaki formülle hesaplarız:

$P_{98}=475+\cfrac{\displaystyle\frac{98\cdot (500+1)}{100}-442}{58}\cdot 25=496,11$

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Yüzdelikler nedir?

Yüzdelikler nasıl hesaplanır

Yüzdelik Hesaplama Örnekleri

örnek 1

Örnek 2

yüzdelik hesaplayıcı

Gruplandırılmış verilerdeki yüzdelikler

yazar hakkında

Dr.benjamin anderson

Yorum ekle