Farklı dağılımlara ait z puanlarının karşılaştırılması

Z-puanı, tek bir veri değerinin ortalamadan ne kadar standart sapma düştüğünü gösterir. Aşağıdaki şekilde hesaplanır:

z-puanı = (x – μ) / σ

Altın:

• x: bireysel veri değeri
• μ: nüfus ortalaması
• σ: popülasyon standart sapması

Bireysel bir değere ilişkin z-puanı şu şekilde yorumlanabilir:

• Pozitif z-puanı: Bireysel değer ortalamanın üzerindedir.
• Negatif z-puanı: Bireysel değer ortalamanın altındadır.
• Z-puanı 0: bireysel değer ortalamaya eşittir.

Z puanları, iki farklı dağılımdaki iki veri noktasının göreceli konumunu karşılaştırmak istediğimizde özellikle faydalıdır. Bunu açıklamak için aşağıdaki örneği inceleyin.

Örnek: Z Puanlarını Karşılaştırma

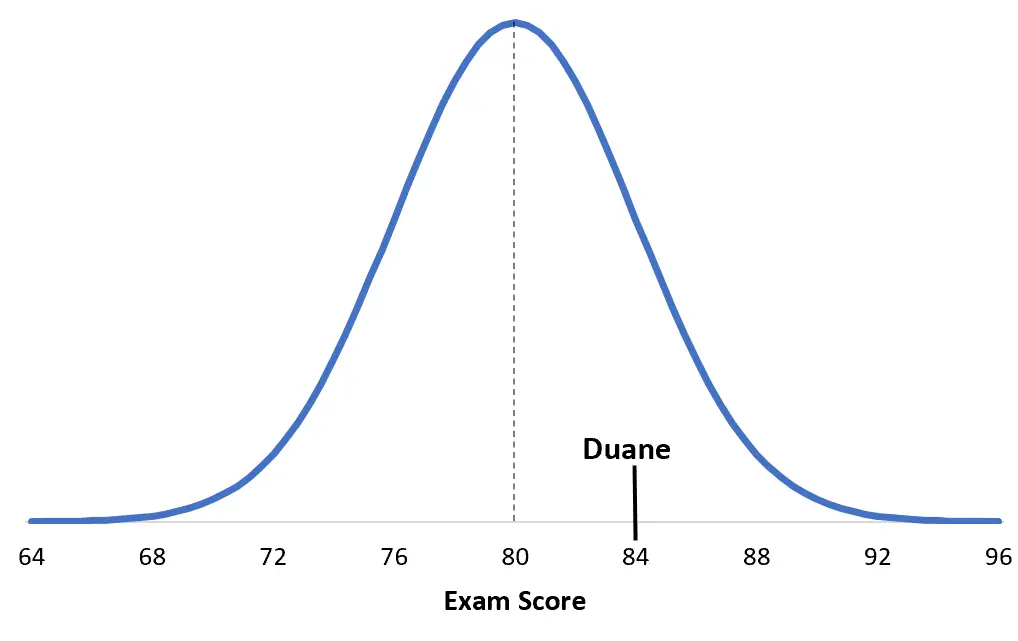
Belirli bir üniversite sınavındaki puanlar ortalama μ = 80 ve standart sapma σ = 4 ile normal olarak dağıtılır. Duane bu sınavdan 84 puan alır.

Başka bir üniversite sınavındaki puanlar ortalama μ = 85 ve standart sapma σ = 8 ile normal şekilde dağılır. Debbie bu sınavdan 90 alır.

Kendi sınav puanlarının dağılımıyla karşılaştırıldığında, sınavda en iyi sonuçları kim elde etti?

Bu soruyu cevaplamak için her kişinin sınav puanının z-puanını hesaplayabiliriz:

Duane’nin z puanı = (x – μ) / σ = (84 – 80) / 4 = 4 / 4 = 1

Debbie’nin z-puanı = (x – μ) / σ = (90 – 85) / 8 = 5/8 = 0,625

Debbie Daha yüksek puan almasına rağmen Duane’nin puanı, kendi sınavının dağılımıyla karşılaştırıldığında aslında daha yüksektir.

Bunu anlamak için durumu görselleştirmeye yardımcı olur. İşte Duane’nin puanının kendi sınav dökümüyle karşılaştırılması:

İşte Debbie’nin sınav dökümünden aldığı puan:

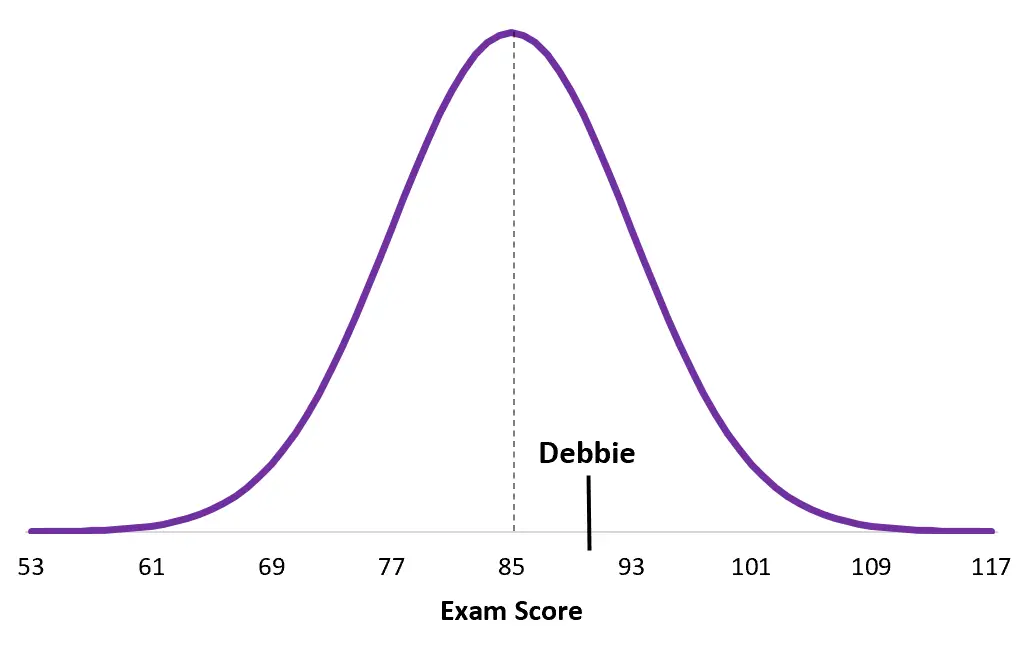
Debbie’nin puanının kendi nüfus ortalamasına Duane’ninkinden ne kadar yakın olduğuna dikkat edin. Genel olarak daha yüksek bir puana sahip olmasına rağmen z-puanı daha düşük çünkü kendi sınavındaki ortalama puan daha yüksek.

Bu örnek, z-puanlarının farklı dağılımlardaki veri değerlerini karşılaştırmak için neden bu kadar yararlı olduğunu göstermektedir: z-puanları, dağılımların ortalama ve standart sapmalarını hesaba katarak farklı dağılımlardaki veri değerlerini karşılaştırmamıza ve hangisinin daha iyi olduğunu görmemize olanak tanır. kendi dağılımlarına göre daha yüksektir.

Ek kaynaklar

Z puanı hesaplayıcı
Z Puanı Hesaplayıcıyı Karşılaştırın