Kovaryans

İle Dr.benjamin anderson Ağustos 5, 2023 İstatistik 0 Yorum

Bu makalede kovaryansın ne olduğu ve nasıl hesaplandığı açıklanmaktadır. Kovaryans formülünün yanı sıra bir veri kümesinin kovaryansının hesaplanmasına ilişkin bir örnek bulacaksınız. Ek olarak, sondaki çevrimiçi hesap makinesini kullanarak herhangi bir veri serisinin kovaryansını hesaplayabilirsiniz.

Kovaryans nedir?

İstatistikte kovaryans , iki rastgele değişkenin ortak varyasyonunun derecesini gösteren bir değerdir. Başka bir deyişle kovaryans, iki değişken arasındaki bağımlılığı analiz etmek için kullanılır.

Kovaryans, iki değişkenin verileri ile bunların ortalamaları arasındaki farkların çarpımlarının toplamının toplam veri sayısına bölünmesine eşittir.

👉Herhangi bir veri setinin kovaryansını hesaplamak için aşağıdaki hesaplayıcıyı kullanabilirsiniz.

Kovaryans değerinin yorumlanması çok basittir:

Kovaryansın pozitif olması iki değişken arasında bağımlılık olduğu anlamına gelir. Bu nedenle, bir değişkenin değeri arttığında diğer değişken de artar veya bunun tersi de geçerlidir.
Kovaryansın negatif olması iki değişken arasındaki ilişkinin negatif olduğu anlamına gelir. Yani bir değişkenin değeri arttığında diğer değişken azalır ve bunun tersi de geçerlidir.
Kovaryansın sıfır olması (veya değerinin sıfıra yakın olması) iki değişken arasında herhangi bir ilişkinin olmadığı anlamına gelir. Başka bir deyişle, iki rastgele değişken bağımsızdır.

Kovaryans nasıl hesaplanır

Bir veri serisinin kovaryansını hesaplamak için aşağıdaki adımlar gerçekleştirilmelidir:

Her değişkenin ortalamasını ayrı ayrı hesaplayın.
Her değişken için, değerlerinin her biri ile değişkenin ortalaması arasındaki farkı bulun.
Her veri noktası için önceki adımda hesaplanan farkları çarpın.
Önceki adımda elde edilen tüm sonuçları toplayın.
Toplam veri sayısına bölün. Elde edilen değer veri serisinin kovaryansıdır.

Özetle, iki değişken arasındaki kovaryansın hesaplanmasına ilişkin formül aşağıdaki gibidir:

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}$

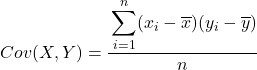
İki değişken arasındaki kovaryansı çıkarmak için şiddetle tavsiye edilen bir yöntem, tüm veri çiftlerini içeren bir tablo oluşturmak ve yukarıda açıklanan adımların her biri için bir sütun eklemektir. Bu şekilde hesaplamalarınız çok daha iyi organize edilecek ve ne yaptığınızı daha iyi anlayacaksınız.

Kovaryans hesaplama örneği

Kovaryansın tanımı göz önüne alındığında, aşağıda bu tür istatistiksel ölçümlerin adım adım hesaplanmasına ilişkin bir örnek verilmiştir. Amaç, kovaryans kavramını ve iki değişken arasındaki korelasyonun nasıl analiz edileceğini daha iyi anlamanızdır.

Aşağıdaki istatistiksel veri setinin kovaryansını hesaplayın:

Öncelikle her değişkenin aritmetik ortalamasını hesaplamamız gerekir. Bunu yapmak için her değişkenin değerlerinin toplamını toplam veri sayısına bölüyoruz.

$\overline{x}=\cfrac{58}{10}=5,8$

$\overline{y}=\cfrac{51}{10}=5,1$

➤ Bakınız: aritmetik formül anlamı

Her rastgele değişkenin ortalamasını belirledikten sonra kovaryansı elde etmek için veri tablosuna aşağıdaki sütunları ekleyebiliriz:

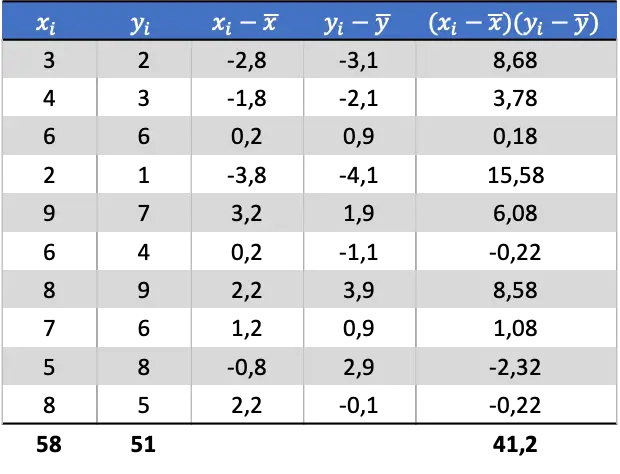
Dolayısıyla iki değişkenin kovaryansını belirlemek için son sütunun toplamını veri çifti sayısına bölmeniz gerekir:

$\begin{aligned}Cov(X,Y)&=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}\\[2ex] Cov(X,Y)&= \cfrac{41,2}{10} \\[2ex]Cov(X,Y)&= 4,12\end{aligned}$

Bu durumda kovaryans değeri pozitiftir; bu, incelenen iki rastgele değişken arasında doğrudan bir bağımlılık olduğu anlamına gelir. Ancak kovaryans değerinin negatif olması iki değişken arasındaki bağımlılığın ters olduğu anlamına gelecektir. Son olarak kovaryans değerinin sıfır olması veya sıfıra çok yakın olması iki değişken arasında doğrusal bir ilişkinin olmadığı anlamına gelir.

Bu örneğin çözümünden de görebileceğiniz gibi sütunları tabloya eklemek ve hesaplamaları hızlı bir şekilde gerçekleştirmek için Excel gibi bir bilgisayar programı kullanmak oldukça faydalıdır. Aksi takdirde işlemleri manuel olarak hesaplayarak kovaryansın bulunması çok daha uzun sürer.

Kovaryans Hesaplayıcı

İki değişken arasındaki kovaryansı hesaplamak için aşağıdaki hesap makinesine bir dizi istatistiksel veri girin. Veri çiftlerini, ilk kutuda yalnızca bir değişkenin değerleri olacak ve ikinci kutuda yalnızca ikinci değişkenin değerleri olacak şekilde ayırmanız gerekir.

Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.

Kovaryans Özellikleri

Kovaryans aşağıdaki özelliklere sahiptir:

Bir rastgele değişken ile bir sabit arasındaki kovaryans sıfırdır.

$Cov(X,a)=0$

Bir değişkenin kendisinin kovaryansı, o değişkenin varyansına eşittir.

$Cov(X,X)=Var(X)$

➤ Bakınız: varyans nedir?

Kovaryans simetri özelliğini karşılar, dolayısıyla X ve Y değişkenlerinin kovaryansı Y ve X değişkenlerinin kovaryansına eşittir. Değişkenlerin sırası kovaryansın sonucunu etkilemez.

$Cov(X,Y)=Cov(Y,X)$

Değişkenler sabitlerle çarpılırsa önce kovaryansı hesaplayabilir, ardından sonucu sabitlerle çarpabilirsiniz.

$Cov(a\cdot X,b\cdot Y)=a\cdot b\cdot Cov(X,Y)$

Değişkenlere terim eklemek kovaryans sonucunu etkilemez.

$Cov(a+X,b+Y)=Cov(X+Y)$

İki rastgele değişken arasındaki kovaryans onların matematiksel beklentileriyle ilgilidir. X ve Y değişkenleri arasındaki kovaryans, X ve Y çarpımının matematiksel beklentisi eksi her değişkenin matematiksel beklentisinin çarpımına eşittir.

$Cov(X,Y)=E[X\cdot Y]-E[X]\cdot E[Y]$

Değişkenlerle çalışırken aşağıdaki cebirsel ifade kovaryansa göre doldurulur:

$\begin{aligned}\displaystyle Cov(aX+bY,cW+dV)= \ & \displaystyle acCov(X,W)+adCov(X,V)+\\[2ex]& +bcCov(Y,W)+bdCov(Y,V)\end{aligned}$

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil