Spss'de basit doğrusal regresyon nasıl gerçekleştirilir

Basit doğrusal regresyon, yordayıcı değişken ile yanıt değişkeni arasındaki ilişkiyi anlamak için kullanabileceğimiz bir yöntemdir.

Bu eğitimde SPSS’de basit bir doğrusal regresyonun nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: SPSS’de Basit Doğrusal Regresyon

Diyelim ki 20 öğrencinin çalışma saatini ve aldığı sınav notunu gösteren aşağıdaki veri setine sahibiz:

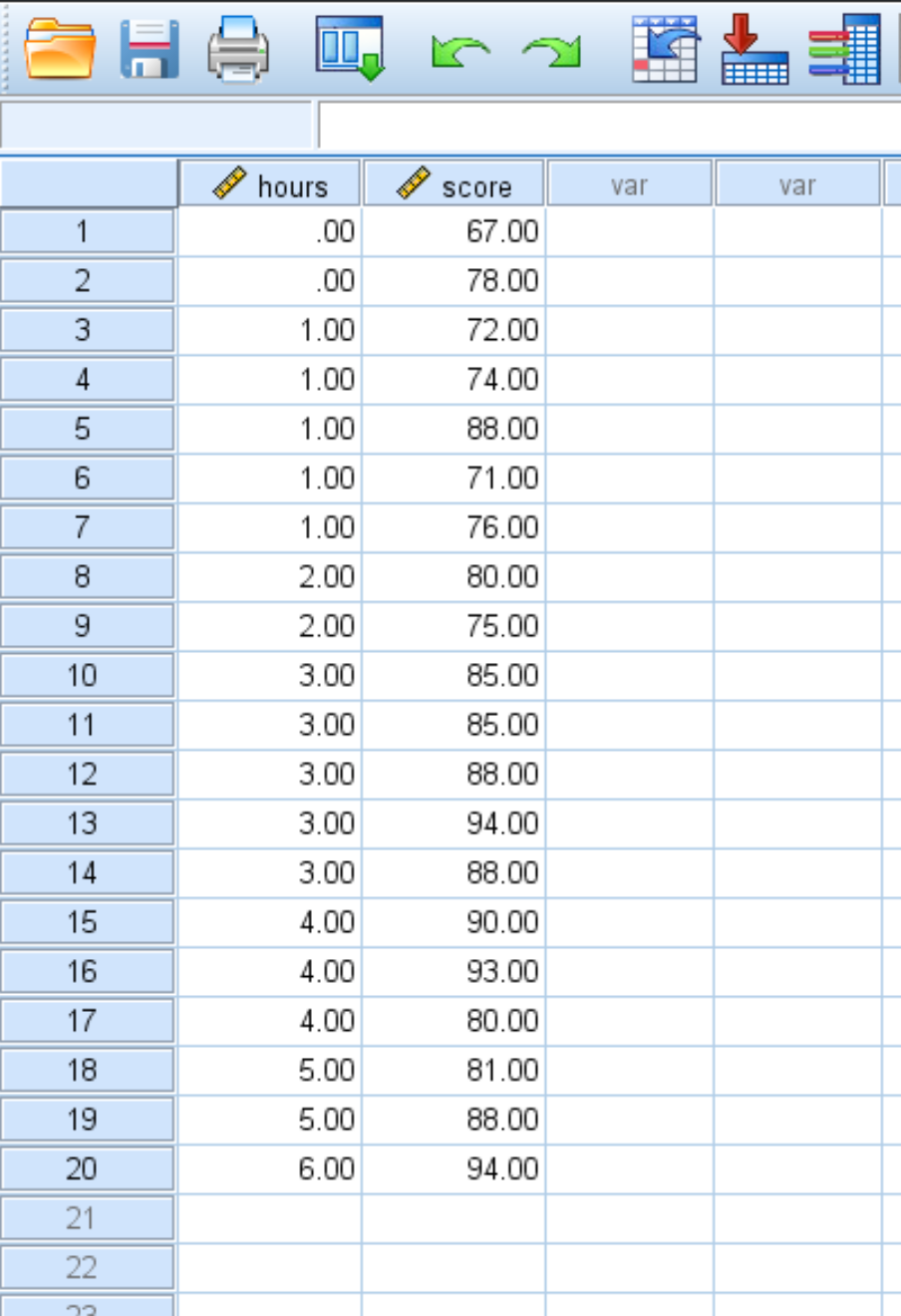
Çalışılan saatlerle sınav puanı arasındaki ilişkiyi ölçmek amacıyla bu veri seti üzerinde basit bir doğrusal regresyon gerçekleştirmek için aşağıdaki adımları kullanın:

Adım 1: Verileri görselleştirin.

İlk olarak, iki değişken arasındaki ilişkinin doğrusal görünmesini sağlamak amacıyla saat ve puan arasındaki ilişkiyi görselleştirmek için bir dağılım grafiği oluşturacağız. Aksi takdirde basit doğrusal regresyon kullanılması uygun bir teknik olmayacaktır.

Grafikler sekmesini ve ardından Grafik Oluşturucu’yu tıklayın:

Şuradan Seç menüsünden, Dağılım/Nokta’ya tıklayın ve ana düzenleme penceresine sürükleyin. Daha sonra değişken süreleri x eksenine ve puanı da y eksenine sürükleyin.

Tamam’ı tıkladığınızda aşağıdaki dağılım grafiği görünecektir:

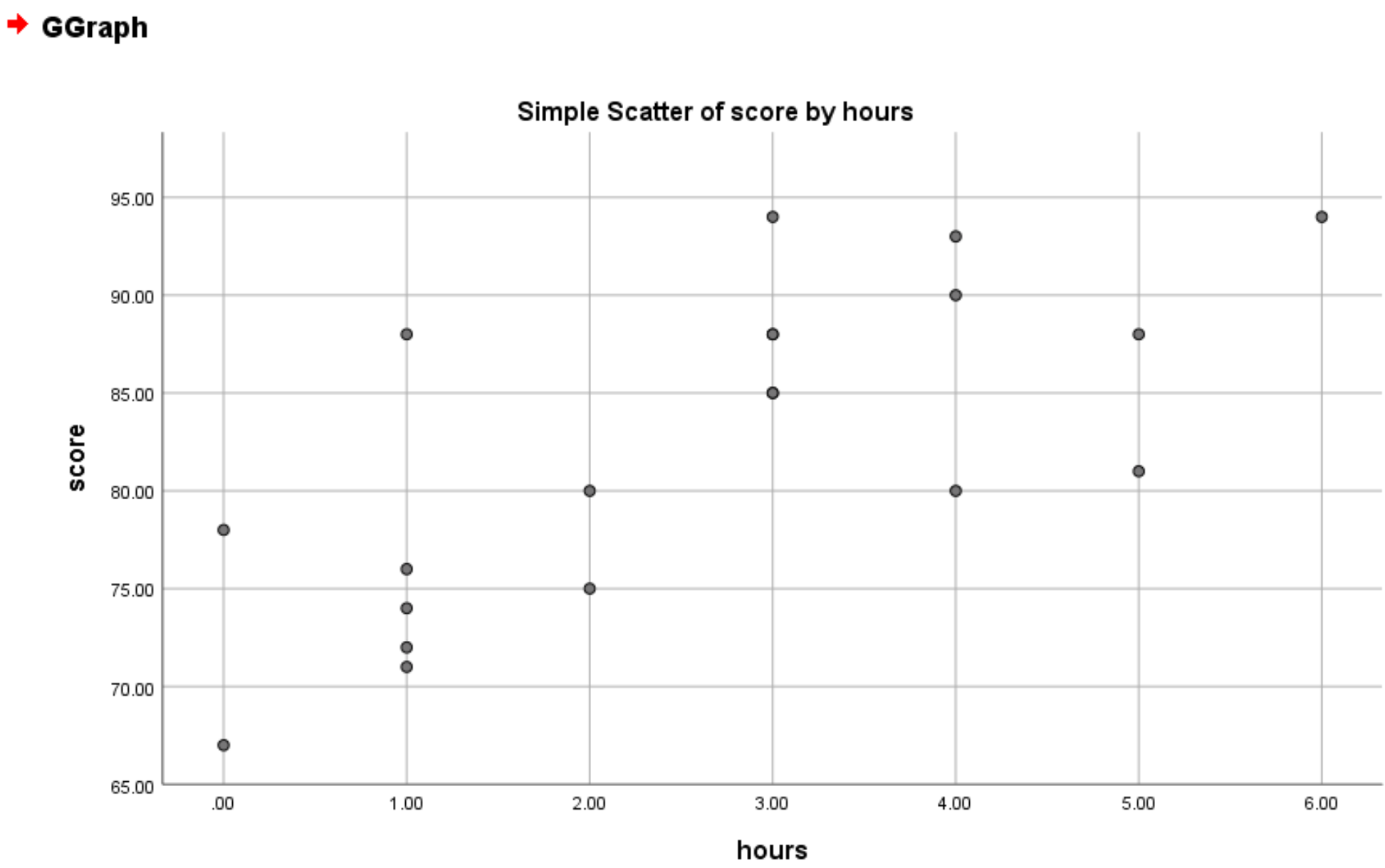
Grafikten saat ile puan arasında pozitif doğrusal bir ilişki olduğunu görebiliriz. Genel olarak, daha fazla saat çalışan öğrenciler daha yüksek puanlara sahip olma eğilimindedir.

İki değişken arasında açık bir doğrusal ilişki olduğundan, veri setine basit bir doğrusal regresyon modeli yerleştirmeye devam edeceğiz.

Adım 2: Basit bir doğrusal regresyon modeli yerleştirin.

Analiz sekmesine, ardından Regresyon’a ve ardından Doğrusal’a tıklayın:

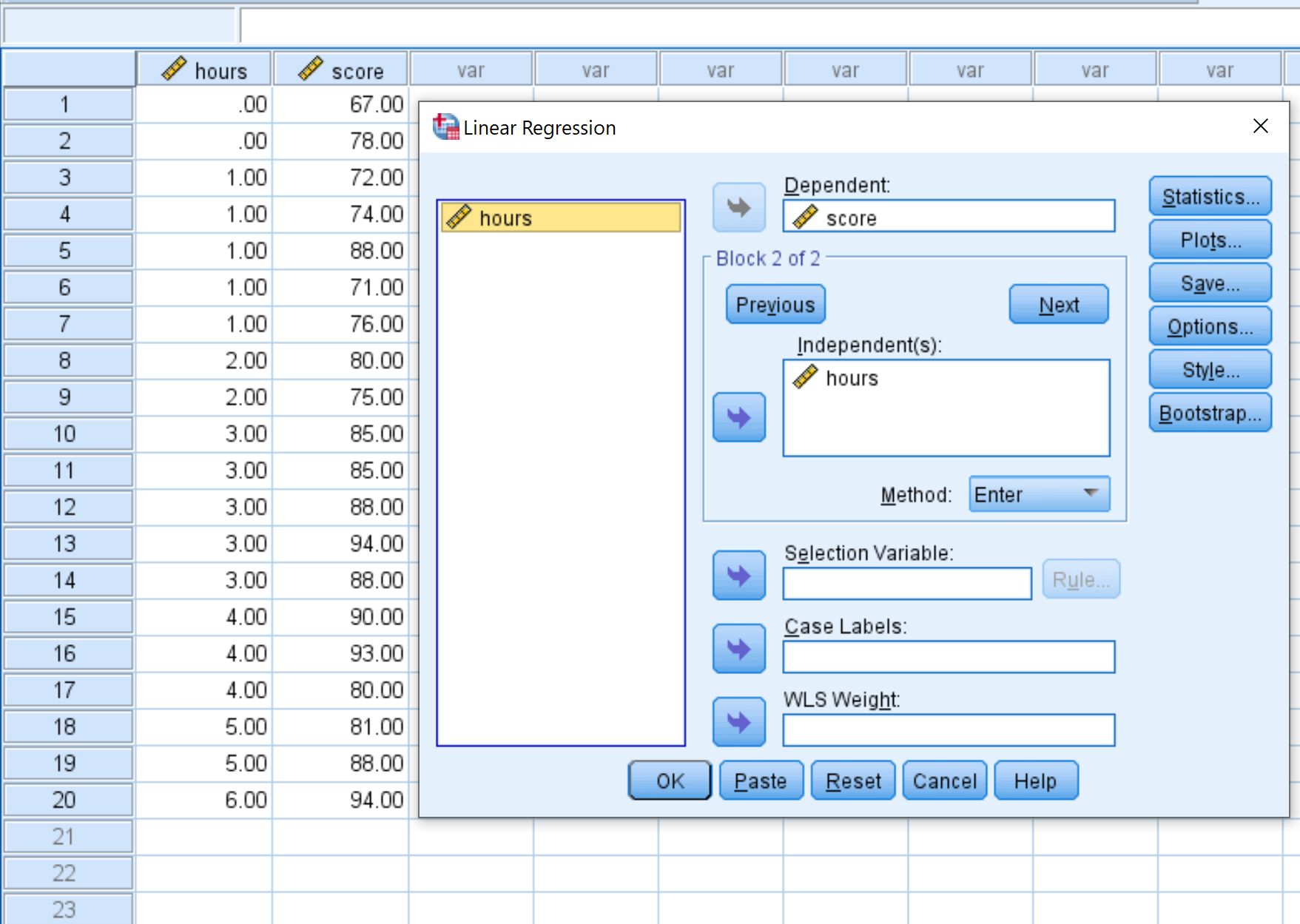
Açılan yeni pencerede değişken puanı Bağımlı etiketli kutuya, saatleri de Bağımsız etiketli kutuya sürükleyin. Daha sonra Tamam’ı tıklayın.

Adım 3: Sonuçları yorumlayın.

Tamam’a tıkladığınızda basit doğrusal regresyon sonuçları görünecektir. Bizi ilgilendiren ilk tablo Model Özeti başlıklı tablodur:

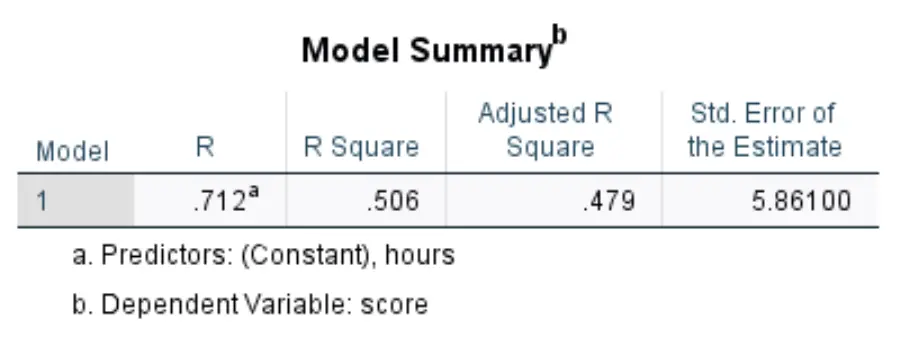
Bu tablodaki en alakalı sayıları nasıl yorumlayacağınız aşağıda açıklanmıştır:

• R Kare: Yanıt değişkenindeki açıklayıcı değişken tarafından açıklanabilen varyansın oranıdır. Bu örnekte sınav puanlarındaki değişimin %50,6’sı çalışılan saatlerle açıklanabilir.
• Standart. Tahmin hatası: Standart hata , gözlemlenen değerler ile regresyon çizgisi arasındaki ortalama mesafedir. Bu örnekte gözlemlenen değerler regresyon doğrusundan ortalama 5.861 birim sapmaktadır.

Bizi ilgilendiren aşağıdaki tablo Katsayılar başlığını taşımaktadır:

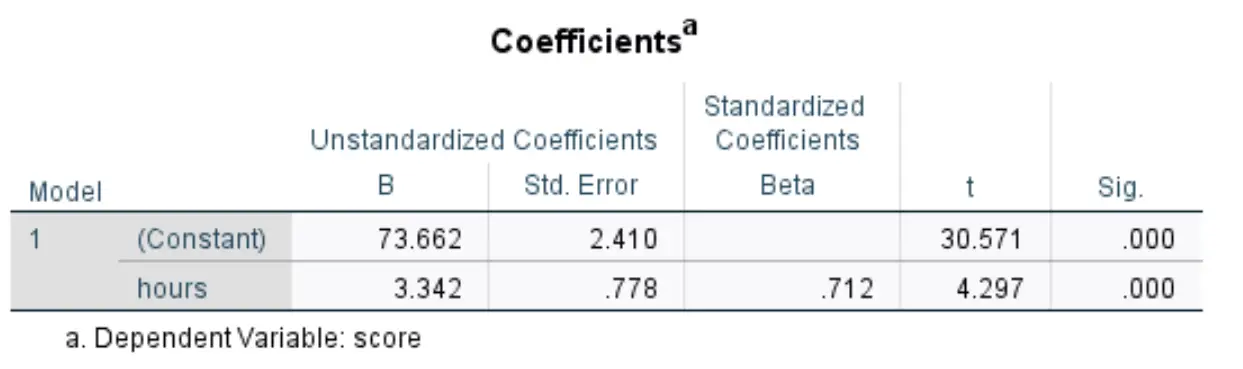
Bu tablodaki en alakalı sayıları nasıl yorumlayacağınız aşağıda açıklanmıştır:

• Standartlaştırılmamış B (Sabit) : Bu bize, yordayıcı değişken sıfır olduğunda yanıt değişkeninin ortalama değerini söyler. Bu örnekte çalışılan saatler sıfır olduğunda ortalama sınav puanı 73.662’dir .
• B standartlaştırılmamış (saat): bu bize, yordayıcı değişkendeki bir birimlik artışla ilişkili yanıt değişkenindeki ortalama değişikliği anlatır. Bu örnekte, çalışılan her ek saat, sınav puanında ortalama 3.342 puanlık bir artışla ilişkilidir.
• Sig (saat): Bu, saatler boyunca test istatistiğiyle ilişkili p değeridir . Bu durumda bu değer 0,05’ten küçük olduğundan saat değişkeninin istatistiksel olarak anlamlı olduğu sonucuna varabiliriz.

Son olarak sabit ve saat değerlerini kullanarak bir regresyon denklemi oluşturabiliriz. Bu durumda denklem şu şekilde olacaktır:

Tahmini sınav puanı = 73.662 + 3.342*(saat)

Bir öğrencinin çalışılan saat sayısına bağlı olarak tahmini sınav puanını bulmak için bu denklemi kullanabiliriz.

Örneğin 3 saat ders çalışan bir öğrencinin sınav puanının 83.688 olması gerekir:

Tahmini sınav puanı = 73,662 + 3,342*(3) = 83,688

Adım 4: Sonuçları rapor edin.

Son olarak basit doğrusal regresyonumuzun sonuçlarını özetlemek istiyoruz. İşte bunun nasıl yapılacağına dair bir örnek:

Çalışılan saat ile sınav notu arasındaki ilişkiyi ölçmek için basit bir doğrusal regresyon uygulandı. Analizde 20 öğrenciden oluşan bir örneklem kullanılmıştır.

Sonuçlar, çalışılan saat ile sınav notu arasında istatistiksel olarak anlamlı bir ilişki olduğunu (t = 4,297, p < 0,000) ve çalışılan saatlerin sınav notunda açıklanan değişkenliğin %50,6’sını oluşturduğunu gösterdi. sınav.

Regresyon denklemi şu şekilde ortaya çıktı:

Tahmini sınav puanı = 73.662 + 3.342*(saat)

Çalışılan her ek saat, sınav puanında ortalama 3.342 artışla ilişkilidir.

Ek kaynaklar

Aşağıdaki eğitimlerde SPSS’de diğer genel görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

SPSS’de çoklu doğrusal regresyon nasıl gerçekleştirilir
SPSS’de ikinci dereceden regresyon nasıl gerçekleştirilir?
SPSS’de lojistik regresyon nasıl yapılır