Spss'de çoklu doğrusal regresyon nasıl gerçekleştirilir
Çoklu doğrusal regresyon, iki veya daha fazla açıklayıcı değişken ile bir yanıt değişkeni arasındaki ilişkiyi anlamak için kullanabileceğimiz bir yöntemdir.
Bu eğitimde SPSS’de çoklu doğrusal regresyonun nasıl gerçekleştirileceği açıklanmaktadır.
Örnek: SPSS’de Çoklu Doğrusal Regresyon
Çalışmak için harcanan saatlerin ve alınan uygulama sınavlarının sayısının, öğrencinin belirli bir sınavda aldığı notu etkileyip etkilemediğini bilmek istediğimizi varsayalım. Bunu araştırmak için aşağıdaki değişkenleri kullanarak çoklu doğrusal regresyon gerçekleştirebiliriz:
Açıklayıcı değişkenler:
- Çalışılan saatler
- Hazırlık sınavları geçti
Yanıt değişkeni:
- Sınav sonucu
SPSS’de bu çoklu doğrusal regresyonu gerçekleştirmek için aşağıdaki adımları kullanın.
Adım 1: Verileri girin.
20 öğrenci için çalışılan saat sayısı, girilen hazırlık sınavları ve alınan sınav sonuçları için aşağıdaki verileri girin:
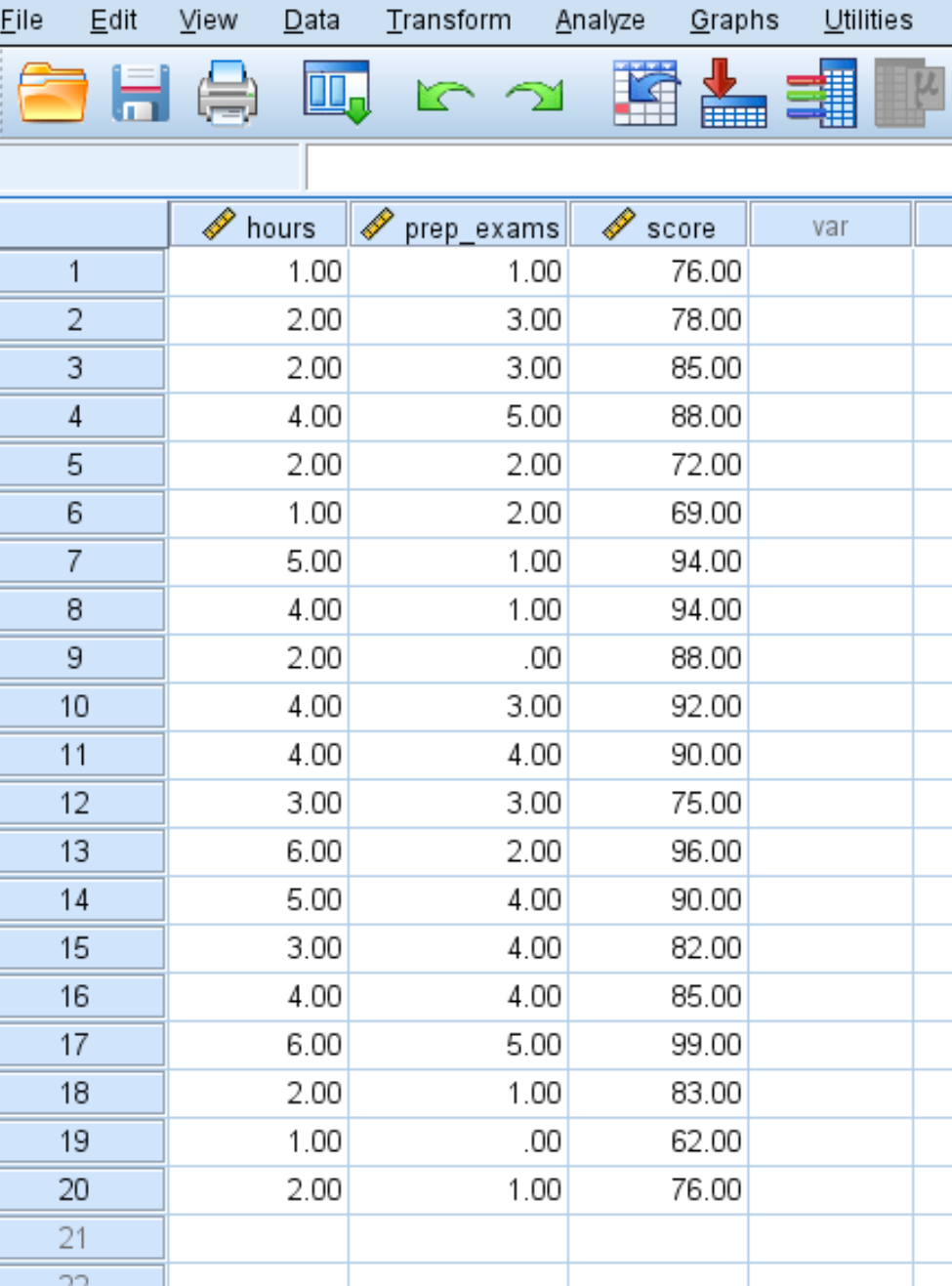
Adım 2: Çoklu doğrusal regresyon gerçekleştirin.
Analiz sekmesine, ardından Regresyon’a ve ardından Doğrusal’a tıklayın:
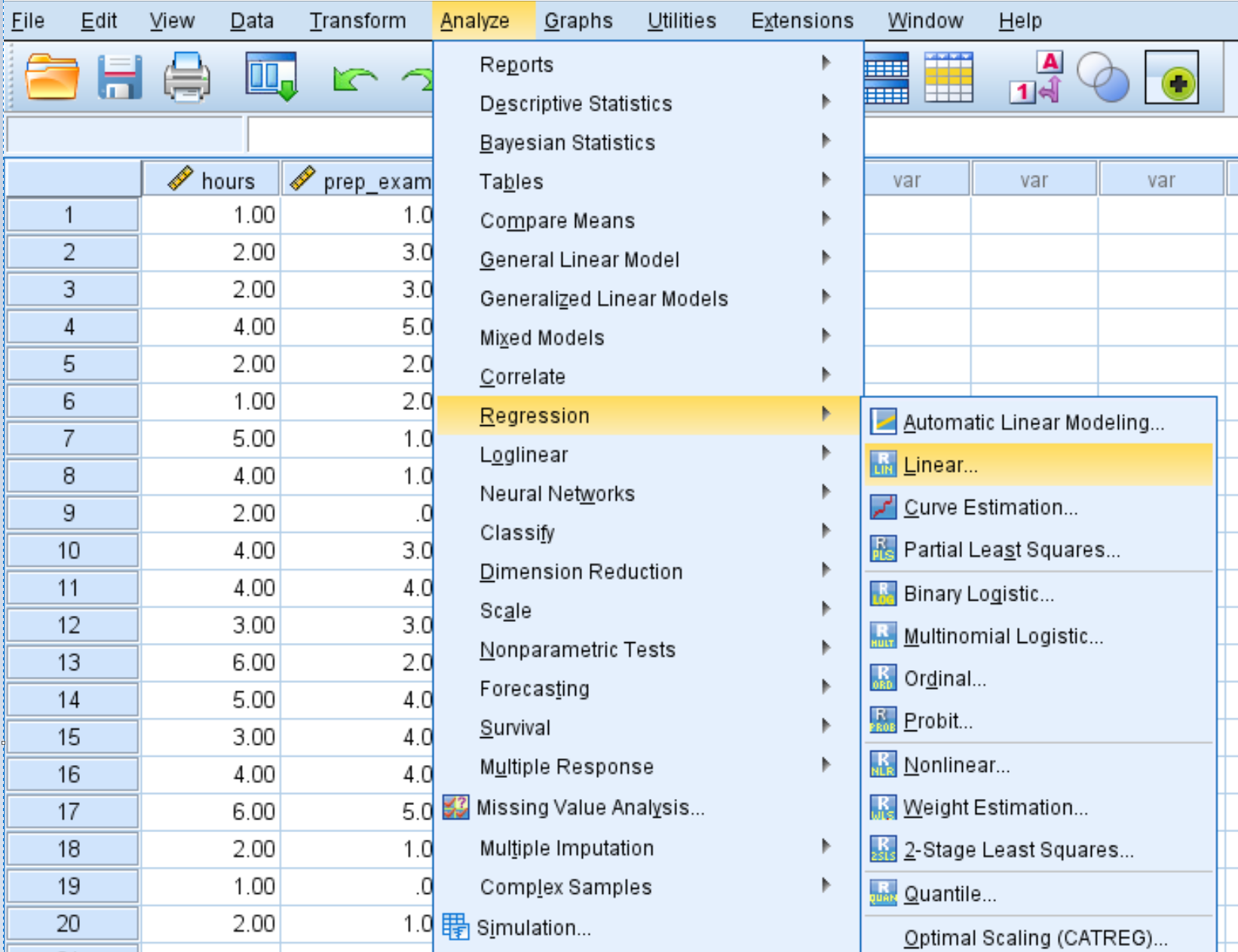
Değişken puanını Bağımlı etiketli kutuya sürükleyin. Hours ve prep_exams değişkenlerini Bağımsız(lar) etiketli kutuya sürükleyin. Daha sonra Tamam’ı tıklayın.
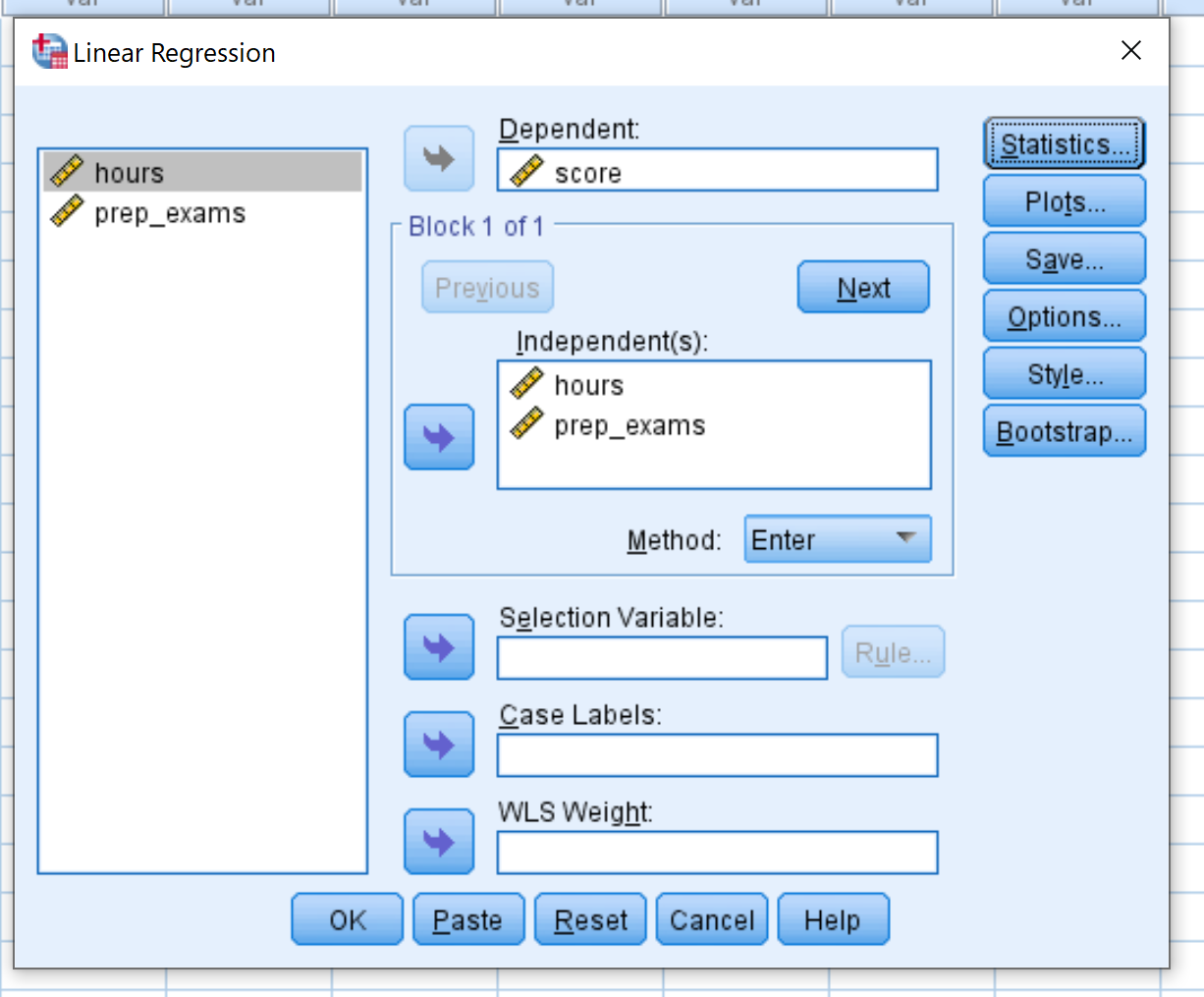
Adım 3: Sonucu yorumlayın.
Tamam’a tıkladığınızda çoklu doğrusal regresyon sonuçları yeni bir pencerede görünecektir.
Bizi ilgilendiren ilk tabloya Model Özeti adı verilir:
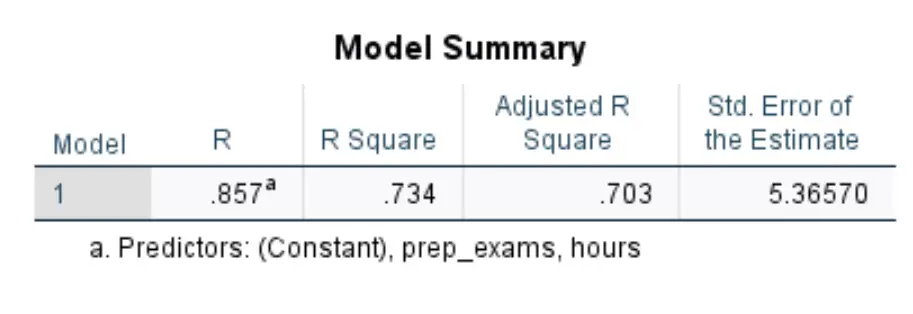
Bu tablodaki en alakalı sayıları nasıl yorumlayacağınız aşağıda açıklanmıştır:
- R Kare: Yanıt değişkenindeki açıklayıcı değişkenler tarafından açıklanabilen varyansın oranıdır. Bu örnekte sınav puanlarındaki farklılığın %73,4’ü çalışılan saat ve girilen hazırlık sınavı sayısıyla açıklanabilir.
- Standart. Tahmin hatası: Standart hata , gözlemlenen değerler ile regresyon çizgisi arasındaki ortalama mesafedir. Bu örnekte gözlemlenen değerler regresyon doğrusundan ortalama 5,3657 birim sapmaktadır.
Bizi ilgilendiren bir sonraki tabloya ANOVA adı veriliyor:
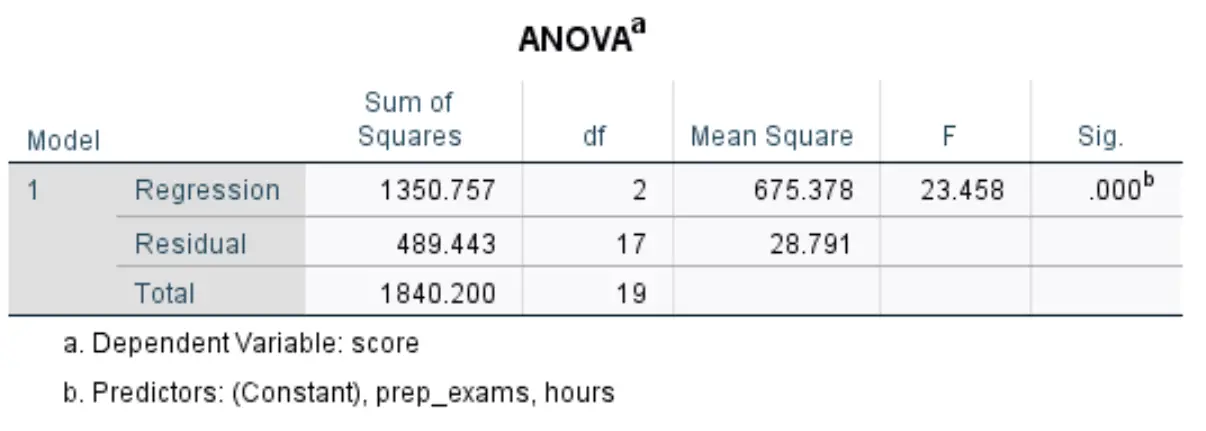
Bu tablodaki en alakalı sayıları nasıl yorumlayacağınız aşağıda açıklanmıştır:
- F: Bu, Regresyon modeli için Ortalama Kare Regresyon / Ortalama Kareler Artık olarak hesaplanan genel F istatistiğidir.
- Sig: Bu, genel F istatistiğiyle ilişkili p değeridir. Bu bize regresyon modelinin bir bütün olarak istatistiksel olarak anlamlı olup olmadığını söyler. Başka bir deyişle, bize iki açıklayıcı değişkenin birleşiminin yanıt değişkeni ile istatistiksel olarak anlamlı bir ilişkiye sahip olup olmadığını söyler. Bu durumda p değeri 0,000’e eşittir; bu, açıklayıcı değişkenlerin, çalışılan saatlerin ve girilen hazırlık sınavlarının sınav sonucuyla istatistiksel olarak anlamlı bir ilişkiye sahip olduğunu gösterir.
Bizi ilgilendiren aşağıdaki tablo Katsayılar başlığını taşımaktadır:
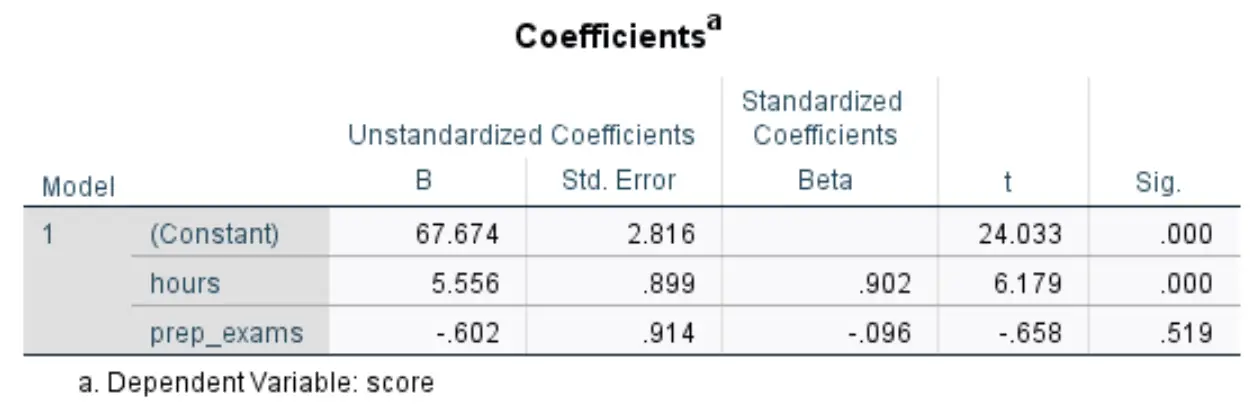
Bu tablodaki en alakalı sayıları nasıl yorumlayacağınız aşağıda açıklanmıştır:
- B standartlaştırılmamış (sabit): bu bize, her iki öngörücü değişken de sıfır olduğunda yanıt değişkeninin ortalama değerini söyler. Bu örnekte, çalışılan saat ve alınan hazırlık sınavlarının her ikisi de sıfır olduğunda ortalama sınav puanı 67.674’tür .
- Standartlaştırılmamış B (saat): Bu bize, alınan hazırlık sınavlarının sayısının sabit kaldığı varsayılarak, çalışma saatlerindeki bir birimlik artışla ilişkili olarak sınav puanlarındaki ortalama değişimi belirtir. Bu durumda, alınan deneme sınavlarının sayısının sabit kaldığı varsayıldığında, ders çalışmak için harcanan her ilave saat, sınav puanında 5.556 puanlık bir artışla ilişkilidir.
- Standartlaştırılmamış B (prep_exams): Bu, çalışılan saat sayısının sabit kaldığı varsayılarak, alınan hazırlık sınavlarındaki bir birimlik artışla ilişkili olarak sınav puanındaki ortalama değişikliği belirtir. Bu durumda, çalışılan saat sayısının sabit kaldığı varsayıldığında, alınan her ek hazırlık sınavı, sınav puanında 0,602 puanlık bir düşüşe neden olur.
- İmza. (saat): Bu, saat açıklayıcı değişkeninin p değeridir. Bu değer (0,000) 0,05’ten küçük olduğundan çalışılan saatlerin sınav puanlarıyla istatistiksel olarak anlamlı bir ilişkisi olduğu sonucuna varabiliriz.
- İmza. (prep_exams): Bu, prep_exams açıklayıcı değişkeninin p değeridir. Bu değer (0,519) 0,05’ten az olmadığı için girilen hazırlık sınav sayısının sınav sonucuyla istatistiksel olarak anlamlı bir ilişkisi olduğu sonucuna varamayız.
Son olarak sabit , saat ve prep_exams için tabloda gösterilen değerleri kullanarak bir regresyon denklemi oluşturabiliriz. Bu durumda denklem şu şekilde olacaktır:
Tahmini sınav puanı = 67,674 + 5,556*(saat) – 0,602*(prep_exams)
Bu denklemi, bir öğrencinin çalışma saati ve girdiği deneme sınavı sayısına göre tahmini sınav puanını bulmak için kullanabiliriz. Örneğin 3 saat ders çalışıp 2 hazırlık sınavına giren bir öğrencinin sınav puanının 83,1 olması gerekir:
Tahmini sınav puanı = 67,674 + 5,556*(3) – 0,602*(2) = 83,1
Not: Hazırlık sınavlarına ilişkin açıklayıcı değişken istatistiksel olarak anlamlı bulunmadığından, onu modelden çıkarmaya ve bunun yerine tek açıklayıcı değişken olarak çalışılan saatleri kullanarak basit bir doğrusal regresyon gerçekleştirmeye karar verebiliriz.