Pearson korelasyon katsayısı
Bu makalede Pearson korelasyon katsayısının (veya doğrusal korelasyon katsayısının) ne olduğu ve ne için kullanıldığı açıklanmaktadır. Pearson korelasyon katsayısını nasıl hesaplayacağınızı adım adım bir alıştırmayla keşfedeceksiniz. Ek olarak, herhangi bir veri setinin Pearson Korelasyon Katsayısı değerini, sondaki çevrimiçi hesaplayıcıyı kullanarak bulabilirsiniz.
Pearson korelasyon katsayısı nedir?
Doğrusal korelasyon katsayısı veya basitçe korelasyon katsayısı olarak da adlandırılan Pearson korelasyon katsayısı, iki değişken arasındaki ilişkiyi gösteren istatistiksel bir ölçümdür.
İki değişken arasındaki Pearson korelasyon katsayısını hesaplamak için, söz konusu değişkenlerin kovaryansını, varyanslarının çarpımının kareköküne bölmeniz gerekir.
Böylece Pearson korelasyon katsayısı, iki niceliksel rastgele değişken arasındaki doğrusal bağımlılığı ölçmeye çalışır. Öncelikle, değişkenler arasındaki korelasyonu sayısal olarak değerlendirmek karmaşıktır çünkü değişken çiftlerinin arasında daha fazla korelasyon olduğunu belirlemek zordur, eğer pues’ta olduğu gibi Pearson korelasyon katsayısının amacı değişkenler arasındaki ilişkiyi değerlendirebilmek için değişkenler arasındaki ilişkiyi değerlendirmekse aralarında karşılaştırın.
Pearson korelasyon indeksinin değeri -1 ile +1 arasındadır. Aşağıda Pearson korelasyon katsayısı değerinin nasıl yorumlandığını göreceğiz.
Pearson Korelasyon Katsayısı Formülü
İki istatistiksel değişkenin Pearson korelasyon katsayısı, değişkenlerin kovaryansı ile her değişkenin varyansının çarpımının karekökü arasındaki bölüme eşittir.
Bu nedenle Pearson korelasyon katsayısını hesaplama formülü aşağıdaki gibidir:
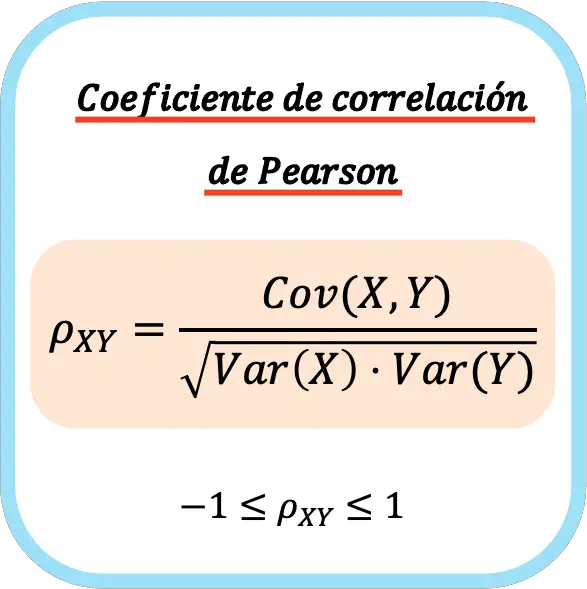
👉Herhangi bir veri seti için Pearson korelasyon katsayısını hesaplamak için aşağıdaki hesap makinesini kullanabilirsiniz.
Pearson korelasyon katsayısı bir popülasyon üzerinde hesaplanırken genellikle Yunanca ρ harfiyle ifade edilir. Ancak katsayı bir örneğe göre hesaplanırken sembol olarak genellikle r harfi kullanılır.
Pearson korelasyon katsayısını belirlemek için iki değişken arasındaki kovaryansı ve bir değişkenin varyansını nasıl hesaplayacağınızı bilmeniz gerektiğini unutmayın. Ayrıca bu istatistiksel ölçümlerin ne anlama geldiğini de anlamalısınız. Bu nedenle açıklamaya devam etmeden önce aşağıdaki iki makalenin okunması tavsiye edilir:
Pearson korelasyon katsayısını hesaplama örneği
Pearson korelasyon katsayısının tanımı ve formülü göz önüne alındığında, nasıl hesaplandığını görebilmeniz için aşağıda adım adım bir örnek verilmiştir.
- Aşağıdaki iki sürekli değişken arasındaki Pearson korelasyon katsayısını hesaplayın:

Pearson korelasyon katsayısını hesaplamadan önce, iki değişken arasındaki ilişkiyi analiz etmek için veri kümesini bir dağılım grafiğinde temsil edeceğiz:
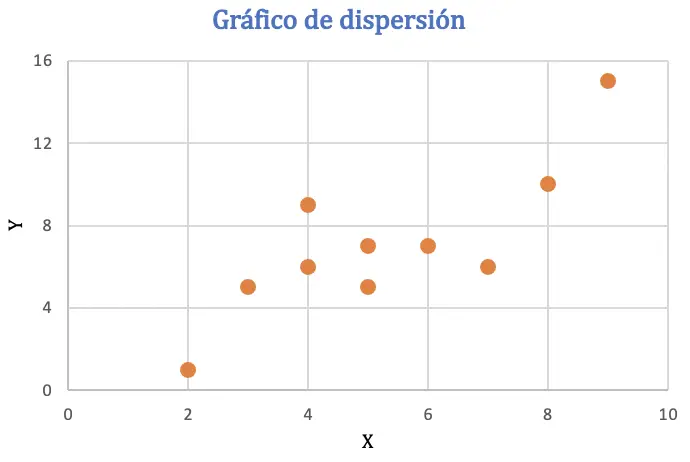
Saçılım grafiğinden verilerin pozitif bir trende sahip olabileceği, yani bir değişkenin değeri arttığında diğer değişkenin de arttığı sonucu çıkarılabilir. Korelasyonu kontrol etmek için Pearson katsayısını bulacağız.
Yapılacak ilk şey, her değişkenin aritmetik ortalamasını ayrı ayrı bulmaktır; bu, verilerin toplam toplamının gözlem sayısına bölünmesine eşdeğerdir.
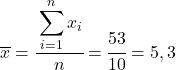
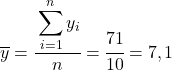
Artık her değişkenin ortalamasını bildiğimize göre, aşağıdaki sütunları veri tablosuna eklememiz gerekiyor:
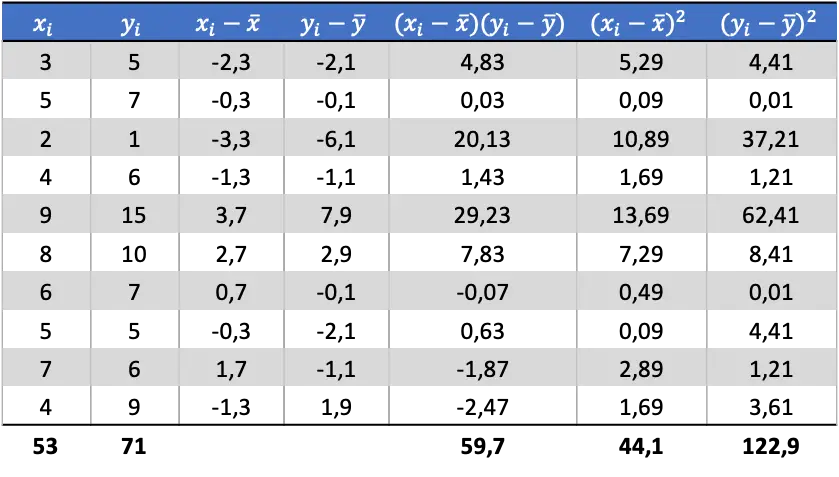
Tabloda hesaplanan verilerden kovaryans ve varyansların değerlerini belirliyoruz (eğer bunun nasıl yapıldığını hatırlamıyorsanız yukarıda bunun ayrıntılı olarak açıklandığı iki bağlantı vardır):
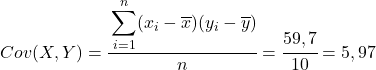
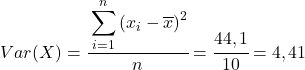
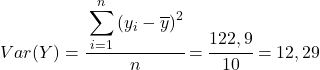
Son olarak, değerini elde etmek için Pearson korelasyon katsayısı formülünü uygulamanız yeterlidir:
![]()
Pearson korelasyon katsayısı 1’e çok yakın bir değere sahiptir, bu da bu iki değişkenin oldukça güçlü bir pozitif korelasyona sahip olduğu anlamına gelir.
Gördüğünüz gibi Pearson korelasyon katsayısını belirlemek için Excel gibi sütun hesaplamalarını daha hızlı yapabilecek programlar kullanmak oldukça faydalıdır.
Pearson Korelasyon Katsayısı Hesaplayıcısı
İki değişken arasındaki Pearson korelasyon katsayısını hesaplamak için aşağıdaki hesap makinesine bir dizi istatistiksel veri girin. Veri çiftlerini, ilk kutuda yalnızca bir değişkenin değerleri olacak ve ikinci kutuda yalnızca ikinci değişkenin değerleri olacak şekilde ayırmanız gerekir.
Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.
Pearson Korelasyon Katsayısını Yorumlamak
Bu bölümde Pearson korelasyon katsayısının nasıl yorumlanacağını göreceğiz çünkü değerini bilmek yeterli değildir ancak anlamını nasıl analiz edeceğinizi bilmeniz gerekir.
Dolayısıyla Pearson korelasyon katsayısının yorumu onun değerine bağlıdır:
- r=-1 : iki değişken mükemmel bir negatif korelasyona sahiptir, dolayısıyla tüm noktaların birbirine bağlandığı negatif eğimli bir çizgi çizebiliriz.
- -1<r<0 : iki değişken arasındaki korelasyon negatiftir, yani bir değişken arttığında diğeri azalır. Değer -1’e ne kadar yakınsa değişkenler o kadar negatif ilişkilidir.
- r=0 : İki değişken arasındaki korelasyon çok zayıftır, aslında aralarındaki doğrusal ilişki sıfırdır. Bu, değişkenlerin bağımsız olduğu anlamına gelmez çünkü doğrusal olmayan bir ilişkiye sahip olabilirler.
- 0<r<1 : İki değişken arasındaki korelasyon pozitiftir, değer +1’e ne kadar yakınsa değişkenler arasındaki ilişki o kadar güçlüdür. Bu durumda bir değişkenin değeri artarken diğerinin değeri artma eğilimindedir.
- r=1 : iki değişken mükemmel pozitif korelasyona sahiptir, yani pozitif doğrusal ilişkiye sahiptirler.
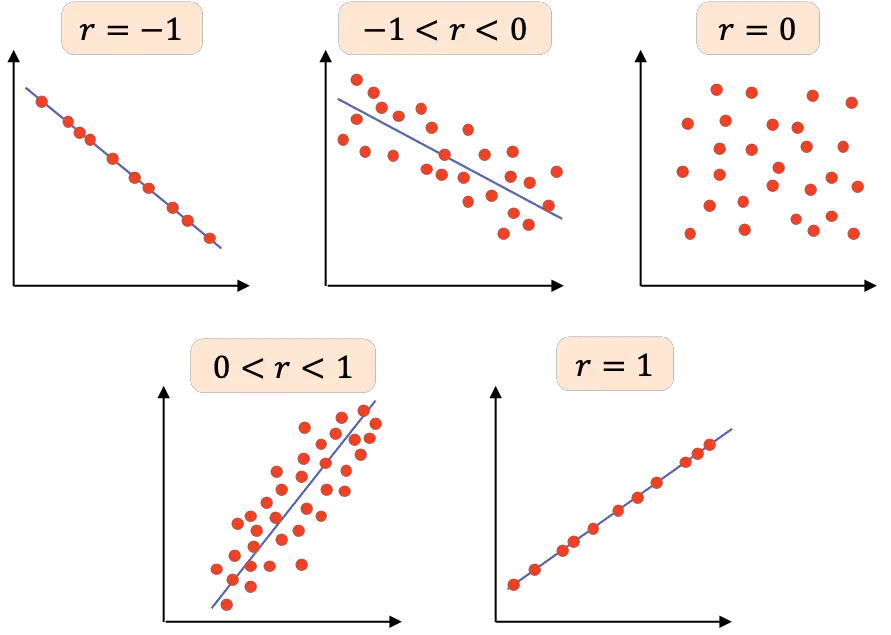
Özetle Pearson korelasyon katsayısının farklı yorumlarıyla aşağıdaki tablo sunulmaktadır:
| Değer | Tercüme |
|---|---|
| r=-1 | Mükemmel negatif korelasyon. |
| -1<r<0 | Negatif korelasyon: Korelasyon -1’e ne kadar yakınsa o kadar güçlüdür. |
| r=0 | Sıfır doğrusal korelasyon. |
| 0<r<1 | Pozitif korelasyon: Korelasyon +1’e ne kadar yakınsa o kadar güçlüdür. |
| r=1 | Mükemmel pozitif korelasyon. |
Unutmayın ki iki değişken arasında ilişki olsa bile bu, aralarında nedensellik olduğu anlamına gelmez; yani iki değişken arasındaki korelasyon, bir değişkendeki değişimin, değişkendeki değişimin nedeni olduğu anlamına gelmez. diğer değişken.
Örneğin vücutta iki farklı hormonun üretimi arasında pozitif bir ilişki olduğunu tespit edersek, bir hormondaki artışın diğer hormonda da artışa yol açması şart değildir. Vücudun her iki hormonu da üretmesi, çünkü bir hastalıkla savaşmak için her ikisine de ihtiyaç duyması ve bu nedenle her ikisinin de düzeylerini aynı anda artırması mümkündür; bu durumda nedeni hastalık olabilir. İki hormon arasında nedensel bir bağlantı olup olmadığının belirlenmesi için daha fazla çalışma yapılması gerekmektedir.