Sas'ta aşamalı regresyon nasıl gerçekleştirilir (örnekle)

Adım adım regresyon, tahmin edicileri modele adım adım girerek ve çıkararak bir dizi tahmin değişkeninden bir regresyon modeli oluşturmak için kullanabileceğimiz bir prosedürdür. daha fazlasını sil.

Adım adım regresyonun amacı , yanıt değişkeniyle istatistiksel olarak anlamlı bir şekilde ilişkili olan tüm yordayıcı değişkenleri içeren bir regresyon modeli oluşturmaktır.

SAS’ta adım adım regresyon gerçekleştirmek için PROC REG’i SELECTION deyimiyle birlikte kullanabilirsiniz.

Aşağıdaki örnek, pratikte SAS’ta adım adım regresyonun nasıl gerçekleştirileceğini gösterir.

Örnek: SAS’ta Adım Adım Regresyon Gerçekleştirme

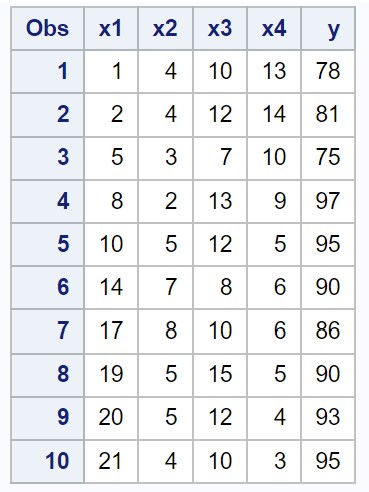
SAS’ta dört öngörücü değişken (x1, x2, x3, x4) ve bir yanıt değişkeni (y) içeren aşağıdaki veri kümesine sahip olduğumuzu varsayalım:

 /*create dataset*/
data my_data;
    input x1 x2 x3 x4 y;
    datalines ;
1 4 10 13 78
2 4 12 14 81
5 3 7 10 75
8 2 13 9 97
10 5 12 5 95
14 7 8 6 90
17 8 10 6 86 
19 5 15 5 90
20 5 12 4 93
21 4 10 3 95
;
run ;

/*view dataset*/
proc print data =my_data;

Şimdi, hangi yordayıcı değişken kombinasyonunun en iyi çoklu doğrusal regresyon modelini üreteceğini belirlemek istediğimizi varsayalım.

“En iyi” regresyon modelinden bahsettiğimizde, belirli önlemleri maksimuma çıkaran veya minimuma indiren modeli kastediyoruz.

Bir grup potansiyel model arasında hangi regresyon modelinin en iyi olduğunu değerlendirmek için yaygın olarak kullandığımız iki ölçüm vardır:

1. Düzeltilmiş R-kare : Ayarlanmış R-kare değeri, bir modeldeki tahminlerin sayısına göre ayarlanan bir modelin kullanışlılığını bize söyler. En yüksek düzeltilmiş R-kare değerine sahip model en iyi model olarak kabul edilir.

2. AIC : Akaike Bilgi Kriteri (AIC), farklı regresyon modellerinin uyumunu karşılaştırmak için kullanılan bir ölçümdür. En düşük AIC değerine sahip model en iyi model olarak kabul edilir.

Neyse ki, SAS’taki regresyon modelleri için hem uygun R-kare hem de AIC değerlerini PROC REG’i SELECTION ifadesi ile kullanarak hesaplayabiliyoruz.

Aşağıdaki kod bunun nasıl yapılacağını gösterir:

 /*perform stepwise multiple linear regression*/
proc reg data =my_data outest =est;
    model y=x1 x2 x3 x4 / selection=adjrsq aic ;
    output out =out p=pr=r;
run ;
quit ; 

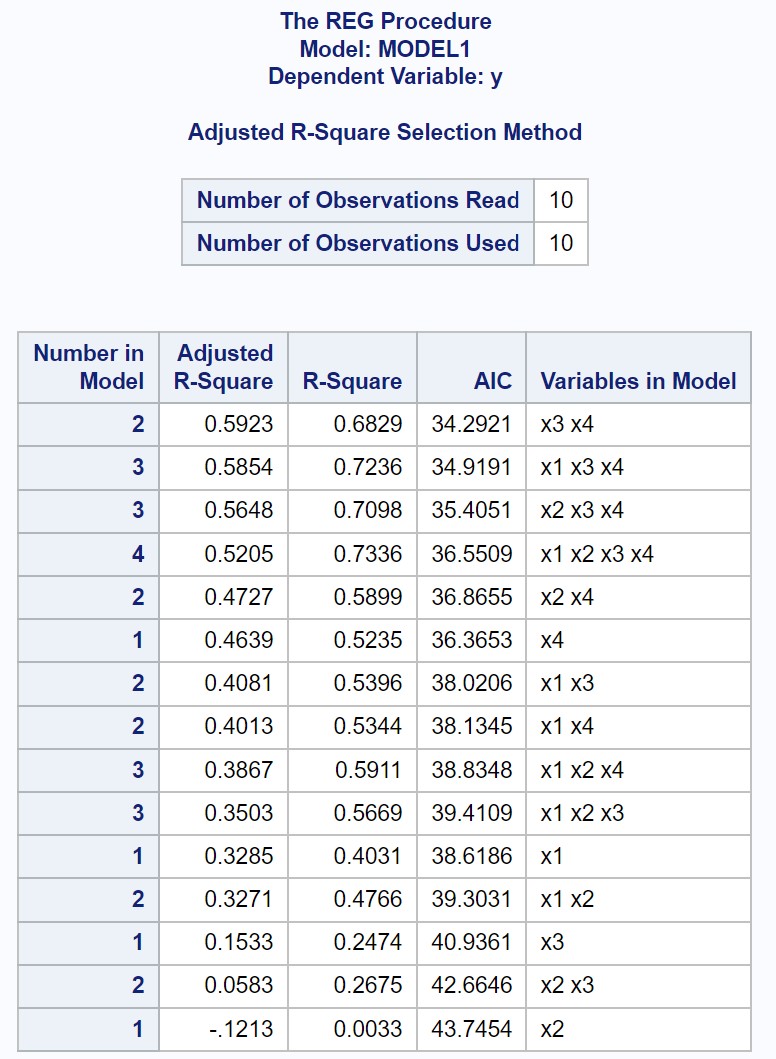
Çıktı, olası her çoklu doğrusal regresyon modeli için uygun R-kare ve AIC değerlerini görüntüler.

Sonuçtan, düzeltilmiş R kare değeri en yüksek ve AIC değeri en düşük olan değerin, yordayıcı değişken olarak yalnızca x3 ve x4’ü kullanan regresyon modeli olduğunu görebiliriz.

Bu nedenle aşağıdaki modelin olası tüm modeller arasında “en iyisi” olduğunu beyan ederiz:

y = b ₀ + b ₁ (x3) + b ₂ (x4)

Bu özel regresyon modeli aşağıdaki ölçümlere sahiptir:

• Düzeltilmiş R-kare değeri: 0,5923
• AIC: 34.2921

“En iyi” regresyon modelinin seçilmesine ilişkin notlar

Bazen en yüksek ayarlanmış R-kare değerine sahip modelin her zaman en düşük AIC değerine sahip olmayabileceğini unutmayın.

Hangi regresyon modelinin en iyi olduğuna karar vermek söz konusu olduğunda düzeltilmiş R-kare ve AIC öneri olarak hizmet eder, ancak gerçek dünyada hangi modelin en iyi olduğunu belirlemek için alan uzmanlığından yararlanmanız gerekebilir.

Ayrıca cimri bir modelin , yani mümkün olduğunca az tahmin değişkeni kullanarak istenen uyum düzeyine ulaşan bir modelin seçilmesi de akıllıca olabilir.

Bu tür bir modelin arkasındaki mantık, en basit açıklamanın muhtemelen doğru olduğunu söyleyen Occam’ın usturası (bazen “tutumluluk ilkesi” olarak da adlandırılır) fikrinden kaynaklanmaktadır.

İstatistiklere uygulandığında, az sayıda parametresi olan ancak tatmin edici düzeyde uyum sağlayan bir model, tonlarca parametresi olan ve yalnızca biraz daha yüksek düzeyde uyum sağlayan bir modele tercih edilmelidir.

Ek kaynaklar

Aşağıdaki eğitimlerde SAS’ta diğer ortak görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

SAS’ta basit doğrusal regresyon nasıl gerçekleştirilir?
SAS’ta çoklu doğrusal regresyon nasıl gerçekleştirilir?
SAS’ta polinom regresyonu nasıl gerçekleştirilir?
SAS’ta lojistik regresyon nasıl gerçekleştirilir?