Ağaç diyagramı

Bu makalede ağaç diyagramının ne olduğu ve nasıl yapıldığı açıklanmaktadır. Böylece ağaç yapılarının örneklerini, bu tür diyagramın avantajlarını ve ayrıca adım adım çözülmüş bir alıştırmayı bulacaksınız.

Ağaç nedir?

Olasılık ağacı olarak da adlandırılan ağaç diyagramı , bir deneyin tüm olası sonuçlarının olasılıklarıyla birlikte grafiksel bir temsilidir.

Bu nedenle, bir örnek uzaydaki tüm olası sonuçların grafiğini çizmek ve olasılıklarını hesaplamak için bir ağaç diyagramı kullanılır.

Bir ağaç diyagramı, nihai sonuçlara ulaşılana kadar her sonucun ( düğüm ) yeni olası sonuçlara ( dallara ) dallanacağı şekilde yapılır.

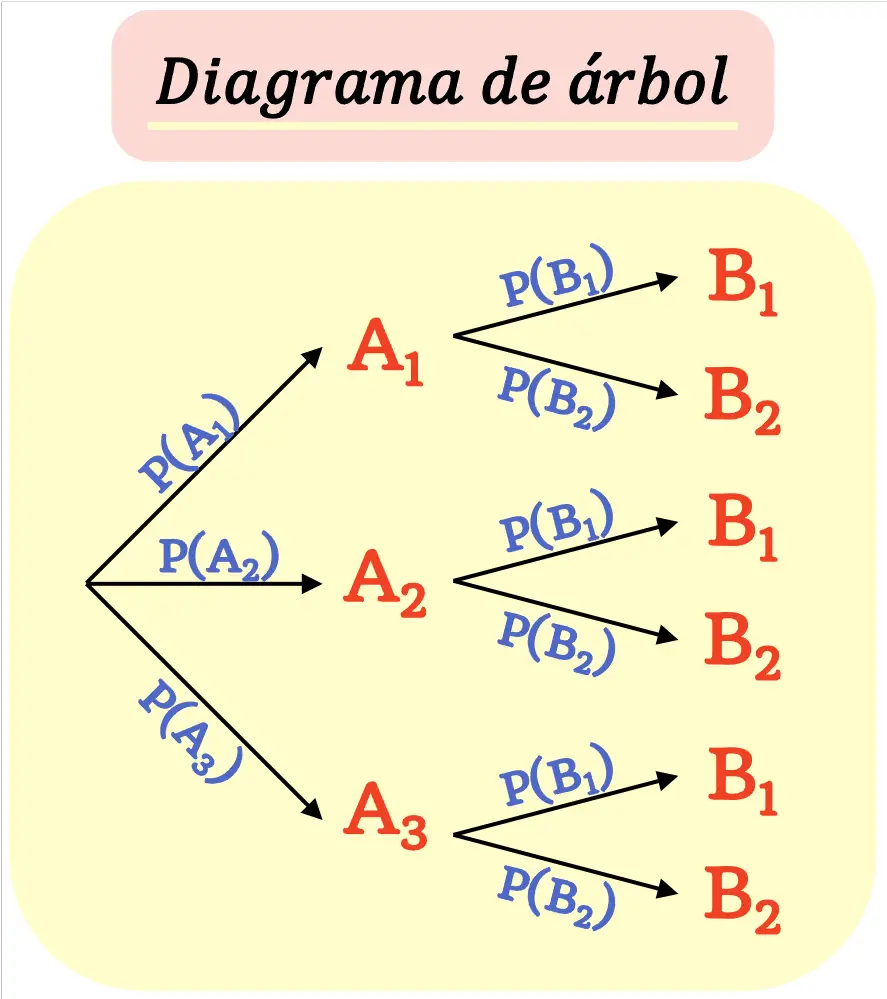
Bir düğümden çıkan tüm dalların olasılıklarının toplamının 1’e eşit olması gerektiği unutulmamalıdır.

Ağaç diyagramı nasıl yapılır

Bir ağaç oluşturmak için aşağıdaki adımları izlemelisiniz:

1. Ağaç diyagramı oluşturmanın ilk adımı her olası sonuç için bir dal çizmektir. Bunlar ilk nesil şubeler olacak.
2. Daha sonra her bir olaya ilişkin olasılık ilgili dalına eklenir.
3. Her birinci nesil dalın sonu, sonraki olası olayların dallarının temsil edilmesi gereken bir düğümdür.
4. İlk dallarda olduğu gibi temsil edilen olayların olasılıklarını eklemeliyiz.
5. Son düğümlere, yani deneyin olası sonlarına ulaşana kadar 3. ve 4. adımları tekrarlayın.

Bir seviyedeki şube sayısının mutlaka farklı bir seviyedeki şube sayısına eşit olması gerekmediğini unutmayın. Aynı şekilde olası bir sonucun ortaya çıkardığı dal sayısı da aynı düzeyde bile değişiklik gösterebilmektedir.

Ağaç örneği

Artık ağaç diyagramı oluşturmanın tanımını ve teorisini bildiğimize göre, kavramı daha iyi anlamak için gerçek dünyadan bir örneğe adım adım bakalım.

• Üç bağımsız paranın yazı tura atılmasının olasılık ağacını oluşturun. Daha sonra üç atışta da tura gelme olasılığını belirleyin.

Kura çekerken yalnızca iki olası sonuç vardır; tura veya yazı gelebilir. Buna göre, bir para atıldığında yazı veya tura gelme olasılığı:

Olası sonuçların olasılıklarını bildiğimizde ağaç diyagramını temsil etmeye devam ederiz.

Yazı-tura atışları bağımsız olduğundan, yazı veya tura gelme olasılığı her atışta her zaman aynı olacaktır. Bu nedenle ağacı oluşturmak için, yapılan her atışta iki dalın (baş ve kuyruk) aynı olasılıkla temsil edilmesi gerekir.

Ve ağacı oluşturduğumuzda tek yapmamız gereken üç yazı tura atmanın olasılığını belirlemek.

Dolayısıyla bu durumda tura gelme olasılıklarının tümünü çarpmamız gerekir çünkü bunlar bizi istenen sonuca götüren yolun olasılıklarıdır.

Böylece, üç yazı tura atışında tura gelme olasılığı şu şekilde hesaplanır:

Kısacası art arda üç kez tura gelme olasılığı %12,5’tir.

Çözülmüş ağaç egzersizi

Bir köyde sadece 3 kreş bulunmaktadır; çocukların %60’ı A kreşine, %30’u B kreşine ve %10’u C kreşine gitmektedir. Ayrıca üç kreşte de nüfusun %55’i kızdır. Ağacı oluşturun ve aşağıdaki olasılıkları hesaplayın:

• Rastgele seçilen bir çocuğun B kreşinden bir kız olma olasılığı.
• Herhangi bir kreşten rastgele seçilen bir çocuğun erkek olma olasılığı.

Tüm kreşlerdeki kızların oranı %55 ise, erkek çocukların yüzdesi basitçe 1 eksi 0,55 çıkarılarak hesaplanır:

Artık tüm olasılıkları bildiğimize göre tüm olasılıkları içeren olasılık ağacını oluşturabiliriz:

Böylece, B kreşinden bir kızın rastgele seçilme olasılığı şu şekilde hesaplanır:

Öte yandan, herhangi bir kreşe erkek çocuk seçme olasılığını belirlemek için önce her kreşe bir erkek çocuk seçme olasılığını bulmalı, sonra bunları toplamalıyız:

Ağaç yapısının avantajları

Ağaç yapısının özelliklerinden dolayı bu tür istatistiksel grafiğin avantajları şunlardır:

• Ağaç diyagramları karar vermede çok faydalıdır.
• Tüm olası sonuçlar arasındaki ilişki grafiksel olarak gösterilebilir.
• Bir sorunun temel nedenini bulmak çok uygundur.
• Olasılık ve istatistik problemlerini çözmeyi kolaylaştırır.
• Ağaç diyagramı fikirleri organize etmeye ve durumu analiz etmeye yardımcı olur.