Ağırlıklı ortalama

İle Dr.benjamin anderson Ağustos 6, 2023 İstatistik 0 Yorum

Burada ağırlıklı ortalamanın ne olduğunu ve nasıl hesaplandığını açıklıyoruz. Ağırlıklı ortalamayı nasıl bulacağımıza dair çözümlü bir alıştırma görebileceksiniz. Üstelik sondaki hesap makinesiyle herhangi bir veri setinin ağırlıklı ortalamasını hesaplayabilirsiniz.

Ağırlıklı ortalama nedir?

Ağırlıklı ortalama, tanımlayıcı istatistiklerin merkeziliğinin bir ölçüsüdür. Ağırlıklı ortalamayı hesaplamak için, önce her istatistiksel veriyi ağırlığıyla (veya ağırlığıyla) çarpmanız, ardından tüm ürünleri toplamanız ve son olarak ağırlıklı toplamı tüm ağırlıkların toplamına bölmeniz gerekir.

Başka bir deyişle ağırlıklı ortalama formülü şu şekildedir:

Burada _xi her bir veri örneğini temsil eder ve _wi buna karşılık gelen ağırlığı temsil eder.

Dolayısıyla bir verinin ağırlığı ne kadar fazlaysa, ağırlıklı ortalamanın hesaplanmasında o kadar önemli hale gelir. Başka bir deyişle, bir veri parçasının ağırlığı ne kadar yüksek olursa, ağırlıklı ortalamanın sonucu da o kadar fazla etkilenecektir.

Ağırlıklı ortalama özellikle notların hesaplanmasında kullanışlıdır çünkü bir ders sırasında yapılan alıştırmaları veya sınavları farklı önemlerle değerlendirmenize olanak tanır. Ağırlıklı ortalama aynı zamanda bir nüfusun fiyatlarını ölçmeye yönelik bir gösterge olan TÜFE’yi (Tüketici Fiyat Endeksi) hesaplamak için de kullanılır.

Ağırlıklı ortalamanın yanı sıra geometrik ortalama, aritmetik ortalama, kare ortalama ve harmonik ortalama gibi başka ortalama türleri de vardır.

Ağırlıklı ortalama nasıl hesaplanır

Ağırlıklı ortalamayı hesaplamak için aşağıdaki adımların izlenmesi gerekir:

Her istatistiksel veriyi karşılık gelen ağırlığıyla çarpın.
Önceki adımda hesaplanan tüm ürünleri toplayın.
Yukarıdaki ağırlıklı toplamı tüm ağırlıkların toplamına bölün.
Elde edilen sonuç istatistiksel numunenin ağırlıklı ortalamasıdır.

👉Herhangi bir veri setinin ağırlıklı ortalamasını hesaplamak için aşağıdaki hesap makinesini kullanabilirsiniz.

Ağırlıklı Ortalama Örneği

Ağırlıklı ortalamanın tanımını göz önünde bulundurarak şimdi bir veri kümesinden ağırlıklı ortalamanın nasıl elde edildiğini tam olarak anlamak için bir alıştırma çözeceğiz.

Bir lise 1. sınıf öğrencisi matematik dersinde şu notları aldı: %30 değerindeki kısmi sınavdan 7, %20 değerindeki grup çalışmasından 9, sınıfta verilen ağırlıklı ağırlıklı alıştırmalardan 6. ağırlığı %40 olan final sınavından %10 ve 8 puan. Konuyla ilgili son notunuz nedir?

Öğrencinin notunu belirlemek için ifadenin verdiği değerlerle ağırlıklı ortalamayı bulmanız gerekir. Bunu yapmak için ağırlıklı ortalama formülünü uyguluyoruz:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+x_3\cdot w_3+x_4\cdot w_4+x_5\cdot w_5}{w_1+w_2+w_3+w_4+w_5}$

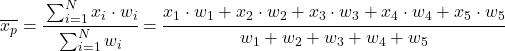
Her teslimatın puanı istatistiksel değerdir ve yüzdesi söz konusu değerin ağırlığına karşılık gelir. Bu nedenle değerleri ve ağırlıkları formülde yerine koyuyoruz ve ağırlıklı ortalama hesaplamasını gerçekleştiriyoruz:

$\overline{x_p}=\cfrac{7\cdot 0,30+9\cdot 0,20+6\cdot 0,10+8\cdot 0,40}{0,30+0,20+0,10+0,40}=7,7$

Dolayısıyla bu öğrencinin final matematik notu 7,7 olacaktır çünkü bu, ağırlıklı ortalamadan elde edilen sonuçtur.

Ağırlıklı Ortalama Hesaplayıcı

Ağırlıklı ortalamasını hesaplamak için herhangi bir istatistiksel örnekten verileri ve bunların ilgili ağırlıklarını aşağıdaki hesap makinesine girin.

İstatistiksel verileri ilk kutuya, ilgili ağırlıklarını ise ikinci kutuya girin. Ağırlıkları verilerle aynı sırada ve ondalık formatta yazmalısınız. Tüm sayılar bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.

Standartlaştırılmış ağırlıklar

Görüldüğü gibi ağırlıklı ortalamada ağırlık, her bir veri parçasına az ya da çok önem vermek için verilen değerdir. Yani eğer bilgi çok önemliyse ağırlığı çok yüksek olacaktır, ancak eğer bilgi çok alakalı değilse ağırlığı çok düşük olacaktır.

Normalleştirilmiş ağırlık, herhangi bir bölme işlemine gerek kalmadan ağırlıklı ortalamayı elde etmek için kullanılan bir ağırlıklandırma türüdür.

Normalleştirilmiş ağırlık, bir veri öğesinin ağırlığının tüm ağırlıkların toplamına bölünmesiyle elde edilir.

$w_i'=\cfrac{w_i}{\sum_{k=1}^N w_k}$

Bu nedenle tüm normalleştirilmiş ağırlıkların toplamı bire eşittir:

$\sum_{i=1}^N w_i'=1$

Dolayısıyla, normalleştirilmiş ağırlıklarla ağırlıklı ortalamayı hesaplamak için her veri öğesini normalleştirilmiş ağırlığıyla çarpmanız yeterlidir:

$\displaystyle\overline{x_p}=\sum_{i=1}^N x_i\cdot w_i'=x_1\cdot w_1'+x_2\cdot w_2'+\dots+x_N\cdot w_N'$

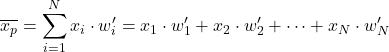
Örneğin verileri 24, 35, 17, 41 ve ağırlıkları 4, 9, 6, 3 olan bir istatistiksel örneğimiz var. Bu veri setinin ağırlıklı ortalamasını bulmak için öncelikle normalleştirilmiş ağırlıkları bölerek hesaplayabiliriz. her ağırlık, tüm ağırlıkların toplamına göre:

$\cfrac{4}{4+9+6+3}=0,18$

$\cfrac{9}{4+9+6+3}=0,41$

$\cfrac{6}{4+9+6+3}=0,27$

$\cfrac{3}{4+9+6+3}=0,14$

Şimdi her veriyi normalleştirilmiş ağırlığıyla çarpın; sonuç ağırlıklı ortalama olacaktır:

$\overline{x_p}=24\cdot 0,18+35\cdot 0,41+17\cdot 0,27+41\cdot 0,14=28,91$

Ağırlıklı ortalama ile aritmetik ortalama arasındaki fark

Benzer işlemlerin yapılması gerektiğinden ağırlıklı ortalama ve aritmetik ortalamanın hesaplanması aynı şekilde yapılır. Ağırlıklı ortalamada her veri noktası ağırlığıyla çarpılır ve ağırlıkların toplamına bölünür, ancak aritmetik ortalamada tüm veriler toplanıp toplam veri noktası sayısına bölünür.

Ağırlıklı ortalama ile aritmetik ortalama arasındaki fark kavramında yatmaktadır, çünkü aritmetik ortalamada tüm verilerin aynı değere sahip olduğu kabul edilir, ancak ağırlıklı ortalamada her veri farklı bir ağırlığa sahiptir.

Tüm ağırlıkların eşit olması durumunda ağırlıklı ortalamanın aritmetik ortalamaya eşit olacağını unutmayın. Matematiksel kanıtını aşağıda görebilirsiniz:

$\begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}$

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil