Ampirik olasılık

Bu yazıda ampirik olasılığın nasıl hesaplanacağını açıklıyoruz. Ampirik olasılığın ne olduğunu, formülünün ne olduğunu, bir örneğini ve ampirik olasılık ile teorik olasılık arasındaki farkların neler olduğunu keşfedeceksiniz.

Ampirik olasılık nedir?

Ampirik olasılık, bir olayın meydana gelme olasılığını gösteren ampirik deneylere veya gerçeklere dayanan istatistiksel bir ölçümdür.

Başka bir deyişle ampirik olasılık, bir deneyin sonuçlarından hesaplanır ve bize bir olayın meydana gelme olasılığını söyler.

Deney ne kadar çok tekrarlanırsa elde edilen ampirik olasılık o kadar kesin olacaktır. Bu nedenle bu tür olasılıklar genellikle binlerce tekrarı simüle eden ve çok kısa sürede analiz edebilen bilgisayar programları kullanılarak belirlenir.

Ampirik olasılık, 0 ile 1 arasında bir sayıdır. Bir olayın meydana gelme olasılığı ne kadar yüksekse, ampirik olasılık da o kadar yüksektir ve bunun tersine, bir olayın meydana gelme olasılığı ne kadar düşükse, ampirik olasılık da o kadar düşüktür.

Ampirik olasılık formülü

Ampirik olasılık formülü, bir deney sırasında bir olayın meydana gelme sayısının deneyin gerçekleştirilme toplam sayısına bölünmesiyle elde edilir.

Örneğin, bir ağaca on farklı kez bakarsak ve ağaçta yedi kez bir kuş görürsek, ağaca bakarken bir kuş görmenin ampirik olasılığı şöyle olacaktır:

Ampirik Olasılık Örneği

Ampirik olasılığın tanımını göz önünde bulundurarak, bu tür olasılıklarla ilgili adım adım bir alıştırma çözeceğiz. Bu şekilde ampirik olasılığın nasıl hesaplandığını görebilirsiniz.

• Bir zarın atılmasıyla ilgili rastgele deneyini oluşturan temel olayların ampirik olasılığını hesaplar.

Öncelikle elde edilen deneysel sonuçları teorik sonuçlarla karşılaştırmanın teorik olasılığını hesaplayacağız. Bir zar atıldığında altı olası sonuç vardır (1, 2, 3, 4, 5 ve 6), dolayısıyla her temel olayın teorik olasılığı şöyledir:

Bu alıştırmayı çözmek için, bir zarın birkaç kez atılmasını simüle etmemiz ve sonuçları bir olasılık tablosuna kaydetmemiz gerekir. Bunun için örneğin Excel programını kullanabiliriz.

Gerçekleştirilen deney sayısının önemini görebilmeniz için, önce on, sonra yüz ve son olarak da bin fırlatmayı simüle edeceğiz. Böylece bir zarın ilk 10 rastgele atışının simülasyonundan elde edilen sonuçlar aşağıdaki gibidir:

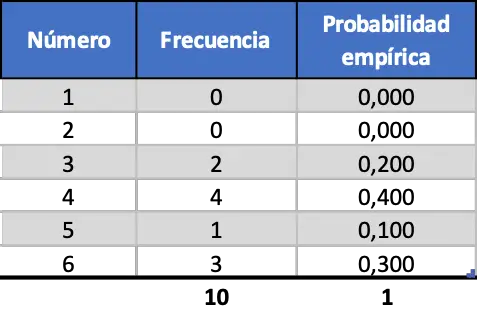
Gördüğünüz gibi sadece on atış simüle edilerek elde edilen ampirik olasılıklar teorik olasılıklara (0,167) yakın değildir.

Ancak deney sayısını artırdıkça bu iki ölçüm daha da benzer hale geliyor, 100 fırlatma simülasyonuna bakın:

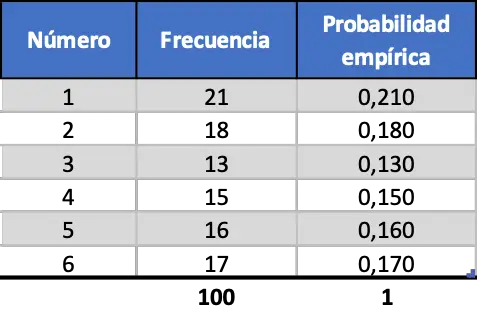
Artık zardaki her sayı için hesaplanan ampirik olasılık teorik olasılığa daha çok benzer, ancak yine de çok farklı değerler elde ediyoruz.

Son olarak aynı işlemi yapıyoruz ancak 1000 başlatmayı simüle ediyoruz:

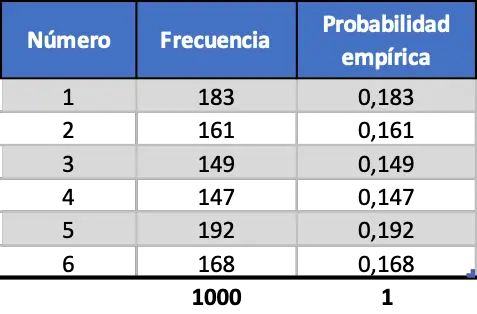
Son beklenmedik durum tablosunda da görebileceğimiz gibi artık ampirik olasılıkların değerleri teorik olasılıklara çok yakın.

Özetle, yapılan deneylerin sayısı ne kadar artarsa, bir olayın ampirik olasılığının değeri o olayın teorik gerçekleşme olasılığına o kadar yakın olacaktır . Bu kural, ne kadar çok veri varsa deneysel değerlerin teorik değerlere o kadar yakın olacağını ifade eden büyük sayılar kanunu olarak tanımlanır.

Ayrıca üç frekans tablosunu karşılaştırdığımızda ampirik olasılığın kesin olmadığını ancak yapılan deney sayısına bağlı olarak değiştiğini görüyoruz. Bu, elde edilen değerleri nasıl yorumlayacağınızı bilmeniz gerektiği anlamına gelir.

Ampirik olasılık ve teorik olasılık

Son olarak ampirik olasılık ve teorik olasılık kavramlarını analiz edeceğiz çünkü bunlar iki tür olasılık olmasına rağmen tamamen farklı anlamlara sahiptirler.

Ampirik olasılık ile teorik olasılık (veya klasik olasılık) arasındaki fark , ampirik olasılığın gerçek deneyimlerden toplanan verilerden hesaplanması, teorik olasılığın ise herhangi bir deney yapılmadan ideal koşullar dikkate alınarak hesaplanmasıdır.

Yani ampirik olasılığı bulmak için bir deneyin simüle edilmesi ve hesaplamanın elde edilen sonuçlara göre yapılması gerekir. Ancak teorik olasılığı bilmek için hiçbir deney yapılmamalı, bunun yerine teorik bir hesaplama yapılmalıdır.

Ek olarak önyargı düzeyi ampirik olasılık ile teorik olasılık arasındaki fark olarak tanımlanır. Önyargı pozitif ya da negatif olabilir, ancak sıfır olması çok zordur çünkü bu, rastgele bir deneyin teorik olasılığa ulaşması anlamına gelir ki bu da pek olası değildir.