Tekrarlanan ölçümlerin manuel olarak gerçekleştirilmesi anova
Tekrarlanan ölçümler ANOVA, her grupta aynı deneklerin yer aldığı üç veya daha fazla grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için kullanılır.
Bu eğitimde, tek yönlü tekrarlanan ölçüm ANOVA’sının manuel olarak nasıl gerçekleştirileceği açıklanmaktadır.
Örnek: Tek yönlü tekrarlanan ölçümler ANOVA’nın elle yapılması
Araştırmacılar üç farklı ilacın farklı reaksiyon sürelerine neden olup olmadığını bilmek istiyorlar. Bunu test etmek için beş hastanın her ilaca tepki süresini (saniye cinsinden) ölçüyorlar. Sonuçlar aşağıda gösterilmektedir:
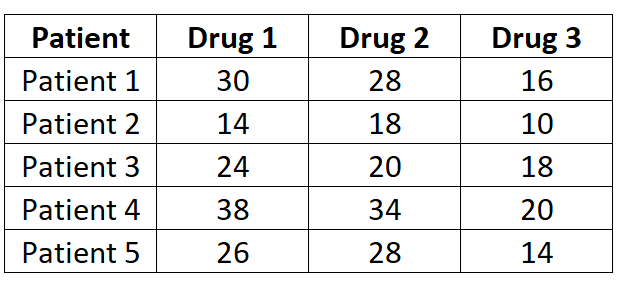
Her hasta üç ilacın her birinde ölçüldüğünden, ortalama reaksiyon süresinin ilaçlar arasında farklılık gösterip göstermediğini belirlemek için tek yönlü tekrarlanan ölçümler ANOVA’sını kullanacağız.
Tekrarlanan ölçümlerin ANOVA’sını manuel olarak gerçekleştirmek için aşağıdaki adımları izleyin:
Adım 1: SST’yi hesaplayın.
İlk olarak, aşağıdaki formülü kullanarak bulunabilecek toplam kareler toplamını (SST) hesaplayacağız:
SST = s 2 toplam (n toplam -1)
Altın:
- s 2 toplam : veri kümesinin varyansı
- n toplam : veri kümesindeki toplam gözlem sayısı
Bu örnekte SST’yi şu şekilde hesaplıyoruz: (64,2667)(15-1) = 899,7
Adım 2: SSB’yi hesaplayın
Daha sonra, aşağıdaki formülü kullanarak bulunabilecek karelerin toplamını (SSB) hesaplayacağız:
SSB = Σn j ( x j – x toplam ) 2
Altın:
- Σ : “toplam” anlamına gelen Yunanca bir sembol
- n j : j’inci gruptaki toplam gözlem sayısı
- x j : j’inci grubun ortalaması
- x toplam : tüm verilerin ortalaması
Bu örnekte SSB’yi şu şekilde hesaplıyoruz: (5)(26,4-22,533) 2 +(5)(25,6-22,533) 2 + (5)(15,6-22,533) 2 = 362,1
Adım 3: SSS’yi hesaplayın.
Daha sonra, aşağıdaki formül kullanılarak bulunabilecek konu kareler toplamını (SSS) hesaplayacağız:
SSS =(Σr 2 k /c) – (N 2 /rc)
Altın:
- Σ : “toplam” anlamına gelen Yunanca bir sembol
- r 2 k : k’inci hastanın kare toplamı
- N: tüm verilerin genel toplamı
- r: toplam hasta sayısı
- c: toplam grup sayısı
Bu örnekte SSS’yi şu şekilde hesaplıyoruz: ((74 2 + 42 2 + 62 2 + 92 2 + 68 2 )/3) – (338 2 /(5)(3)) = 441,1
Adım 4: SES’i hesaplayın.
Daha sonra, aşağıdaki formül kullanılarak bulunabilecek karesel hatanın (SSE) toplamını hesaplayacağız:
SSE = SST – SSB – SSS
Bu örnekte SES’i şu şekilde hesaplıyoruz: 899,7 – 362,1 – 441,1 = 96,5
Adım 5: Tekrarlanan ölçümler ANOVA tablosunu doldurun.
Artık SSB, SSS ve SSE’ye sahip olduğumuza göre tekrarlanan ölçümler ANOVA tablosunu doldurabiliriz:
| Kaynak | Kareler toplamı (SS) | df | Ortalama kareler (MS) | F |
|---|---|---|---|---|
| Arasında | 362.1 | 2 | 181.1 | 15.006 |
| Ders | 441.1 | 4 | 110.3 | |
| Hata | 96.5 | 8 | 12.1 |
Tablodaki farklı sayıları şu şekilde hesapladık:
- df arasında: #gruplar – 1 = 3 – 1 = 2
- df konusu: #katılımcılar – 1 = 5 – 1 = 4
- Hata df: * df konusu = 2*4 = 8 arasında df
- MS girer: SSB / df girer = 362,1 / 2 = 181,1
- MS konusu: SSS konusu / df = 441,1 / 4 = 110,3
- MS hatası: SSE hatası / df = 96,5 / 8 = 12,1
- F: MS girer / MS hatası = 181,1 / 12,1 = 15,006
Adım 6: Sonuçları yorumlayın.
Bu tek yönlü tekrarlanan ölçümler için ANOVA’nın F testi istatistiği 15,006’dır . Bunun istatistiksel olarak anlamlı bir sonuç olup olmadığını belirlemek için bunu F dağılım tablosunda bulunan kritik F değeriyle aşağıdaki değerlerle karşılaştırmamız gerekir :
- α (anlamlılık düzeyi) = 0,05
- DF1 (payın serbestlik derecesi) = df = 2 arası
- DF2 (paydanın serbestlik derecesi) = hata df = 8
F’nin kritik değerinin 4,459 olduğunu bulduk.
ANOVA tablosundaki F testi istatistiği, F dağılım tablosundaki kritik F değerinden büyük olduğundan sıfır hipotezini reddediyoruz. Bu, ilaçların ortalama yanıt süreleri arasında istatistiksel olarak anlamlı bir fark olduğunu söyleyecek yeterli kanıtımız olduğu anlamına geliyor.