Tam kılavuz: sas'ta anova sonuçları nasıl yorumlanır?

Üç veya daha fazla bağımsız grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için tek yönlü ANOVA kullanılır.

Aşağıdaki örnek, SAS’ta tek yönlü ANOVA sonuçlarının nasıl yorumlanacağını gösterir.

Örnek: ANOVA sonuçlarını SAS’ta yorumlama

Bir araştırmacının bir çalışmaya katılmak üzere 30 öğrenciyi işe aldığını varsayalım. Öğrenciler bir sınava hazırlanmak için üç çalışma yönteminden birini kullanmak üzere rastgele atanır .

Her öğrencinin sınav sonuçları aşağıda gösterilmektedir:

Bu veri kümesini SAS’ta oluşturmak için aşağıdaki kodu kullanabiliriz:

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 78
At 81
At 82
At 82
At 85
At 88
At 88
At 90
B 81
B 83
B 83
B85
B 86
B 88
B90
B91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run ;

Daha sonra tek yönlü ANOVA’yı gerçekleştirmek için proc ANOVA’yı kullanacağız:

 /*perform one-way ANOVA*/
proc ANOVA data =my_data;
    classMethod ;
    modelScore = Method;
    means Method / tukey cldiff ;
run ;

Not : Tek yönlü ANOVA’dan elde edilen genel p değeri istatistiksel olarak anlamlıysa, Tukey post-hoc testinin (güven aralıklarıyla) gerçekleştirilmesi gerektiğini belirtmek için, tukey ve cldiff seçenekleriyle birlikte ortalama ifadesini kullandık.

Öncelikle sonuçtaki ANOVA tablosuna bakacağız:

Çıktıdaki her değerin nasıl yorumlanacağı aşağıda açıklanmıştır:

DF modeli: Değişken yöntemin serbestlik derecesi. Bu #groups -1 olarak hesaplanır. Bu durumda 3 farklı çalışma yöntemi vardı, dolayısıyla bu değer: 3-1 = 2 .

DF hatası: artıkların serbestlik derecesi. Bu, #toplam gözlemler – #gruplar olarak hesaplanır. Bu durumda 24 gözlem ve 3 grup olduğundan bu değer: 24-3 = 21 olur.

Düzeltilmiş toplam : DF modelinin ve DF hatasının toplamı. Bu değer 2 + 21 = 23’tür .

Kareler Toplamı Modeli: Değişkene ilişkin karelerin toplamı yöntemi . Bu değer 175.583’tür .

Kareler Toplamı Hatası: Artıklar veya “hatalar” ile ilişkili karelerin toplamı. Bu değer 350,25’tir .

Düzeltilmiş Kareler Toplamı : SS modeli ve SS hatasının toplamı. Bu değer 525.833’tür .

Ortalama kareler modeli: yöntemle ilişkili karelerin ortalama toplamı. Bu, SS modeli / DF modeli veya 175,583 / 2 = 87,79 olarak hesaplanır.

Ortalama kare hatası: artıklarla ilişkili karelerin ortalama toplamı. Bu, SS Hatası / DF Hatası olarak hesaplanır ve bu da 350,25 / 21 = 16,68 olur.

F değeri: ANOVA modelinin genel F istatistiği. Bu, model ortalama karesi/ortalama kare hatası veya 87,79/16,68 = 5,26 olarak hesaplanır.

Pr >F: Pay df = 2 ve payda df = 21 olan F istatistiğiyle ilişkili p değeri. Bu durumda p değeri 0,0140 olur.

Sonuç kümesindeki en önemli değer p değeridir çünkü bize üç grup arasında ortalama değerler arasında anlamlı bir fark olup olmadığını söyler.

Tek yönlü bir ANOVA’nın aşağıdaki boş ve alternatif hipotezleri kullandığını hatırlayın:

• H ₀ (sıfır hipotezi): tüm grup ortalamaları eşittir.
• H _A (alternatif hipotez): En az bir grup ortalaması diğerlerinden farklıdır.

ANOVA tablomuzdaki p değeri (0,0140) 0,05’ten küçük olduğundan sıfır hipotezini reddediyoruz.

Bu, ortalama sınav puanının üç çalışma yöntemi arasında eşit olmadığını söyleyecek yeterli kanıtımız olduğu anlamına gelir.

Tam olarak hangi grup ortalamalarının farklı olduğunu belirlemek için Tukey’in post-hoc testlerinin sonuçlarını gösteren nihai sonuç tablosuna bakmamız gerekir:

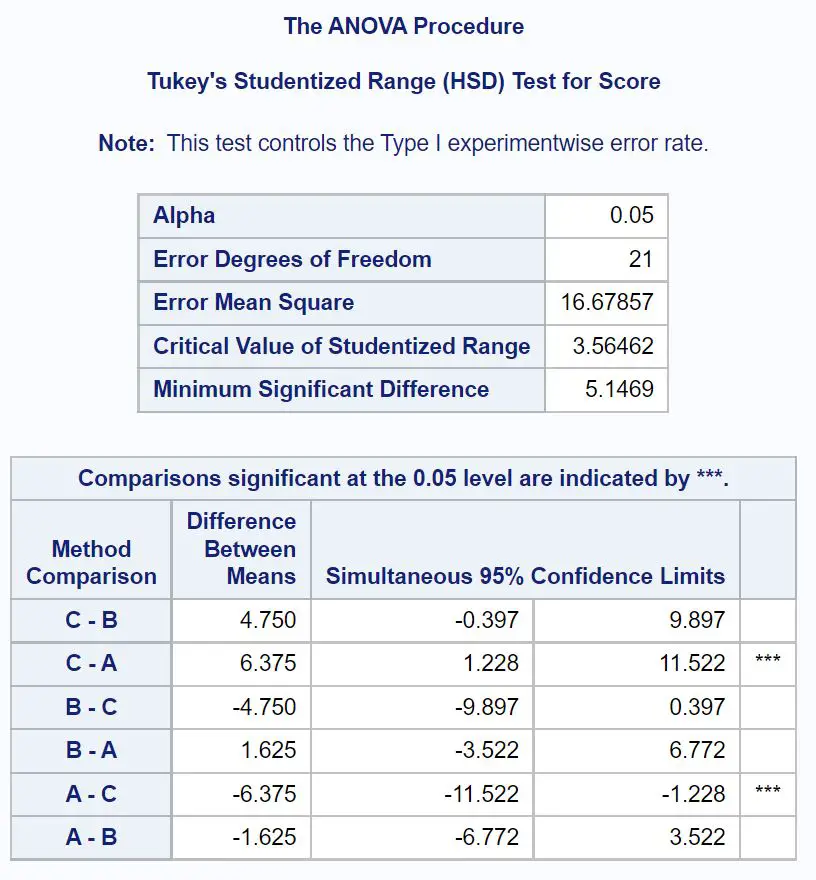
Hangi grup ortalamalarının farklı olduğunu bulmak için hangi ikili karşılaştırmaların yanında yıldız ( *** ) olduğuna bakmamız gerekir.

Tablo A Grubu ile C Grubu arasında ortalama sınav puanları arasında istatistiksel olarak anlamlı bir fark olduğunu göstermektedir.

Spesifik olarak, Grup C ile Grup A arasındaki sınav puanları arasındaki ortalama fark 6.375’tir .

Ortalama fark için %95 güven aralığı [1,228, 11,522]’ dir.

Diğer grupların ortalamaları arasında istatistiksel olarak anlamlı bir fark yoktur.

Ek kaynaklar

Aşağıdaki eğitimler ANOVA modelleri hakkında ek bilgi sağlar:

ANOVA ile Post-Hoc Testini Kullanma Kılavuzu
SAS’ta tek yönlü ANOVA nasıl gerçekleştirilir?
SAS’ta iki yönlü ANOVA nasıl gerçekleştirilir?