Kapsam kısıtlaması nedir?

İstatistiklerde sıklıkla iki değişken arasındaki korelasyonu ölçmeye çalışırız. Bu, aşağıdakileri anlamamıza yardımcı olur:

• İki değişken arasındaki ilişkinin yönü . Değişkenlerden biri artarken diğer değişken artma mı yoksa azalma mı eğilimindedir?
• İki değişken arasındaki ilişkinin gücü . İki değişkenin değeri ne kadar değişir?

Ne yazık ki, iki değişken arasındaki korelasyon ölçülürken ortaya çıkabilecek soruna aralık kısıtlaması denir. Bu, değişkenlerden birinin ölçülen değer aralığının bir nedenden dolayı kısıtlanması durumunda ortaya çıkar.

Örneğin, belirli bir okuldaki öğrencilerin ders çalışma saatleri ile sınav puanları arasındaki ilişkiyi ölçmek istediğimizi varsayalım.

Okuldaki 1000 öğrencinin tamamı için bu iki değişkene ilişkin veri toplarsak, çalışılan saatlerle sınav puanları arasındaki korelasyonun 0,73 olduğunu bulabiliriz.

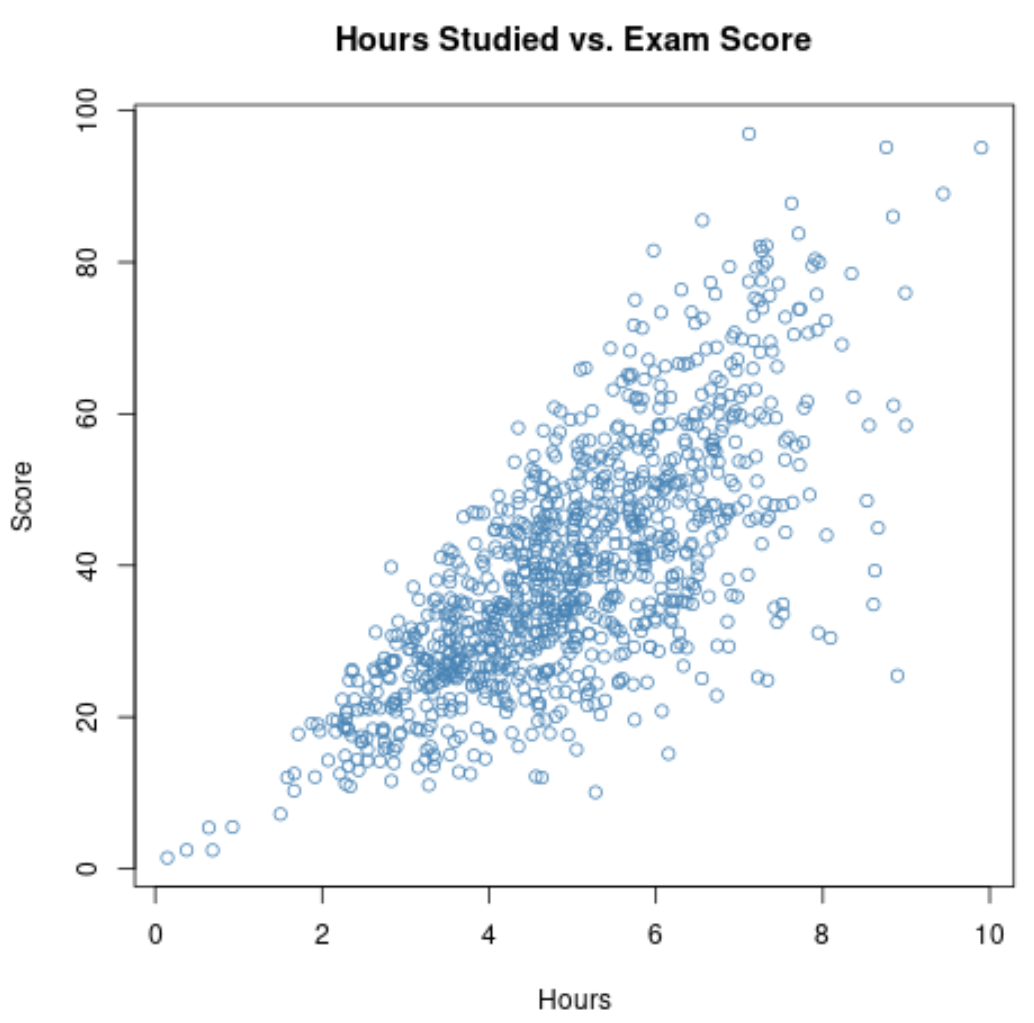
Bu korelasyonun oldukça yüksek olması, iki değişken arasında güçlü bir pozitif ilişkiye işaret etmektedir. Öğrenciler daha fazla çalıştıkça sınavlarda daha iyi performans gösterme eğilimi gösterirler.

Ancak sadece üstün başarı derslerindeki öğrenciler hakkında veri topladığımızı varsayalım. Bu öğrencilerin tamamı en az 6 saat ders çalışmış olabilir.

Dolayısıyla, bu öğrencilerin çalışılan saatlerle sınav puanları arasındaki ilişkiyi hesaplarsak, çalışılan değişken saatler için dar bir aralık kullanırız.

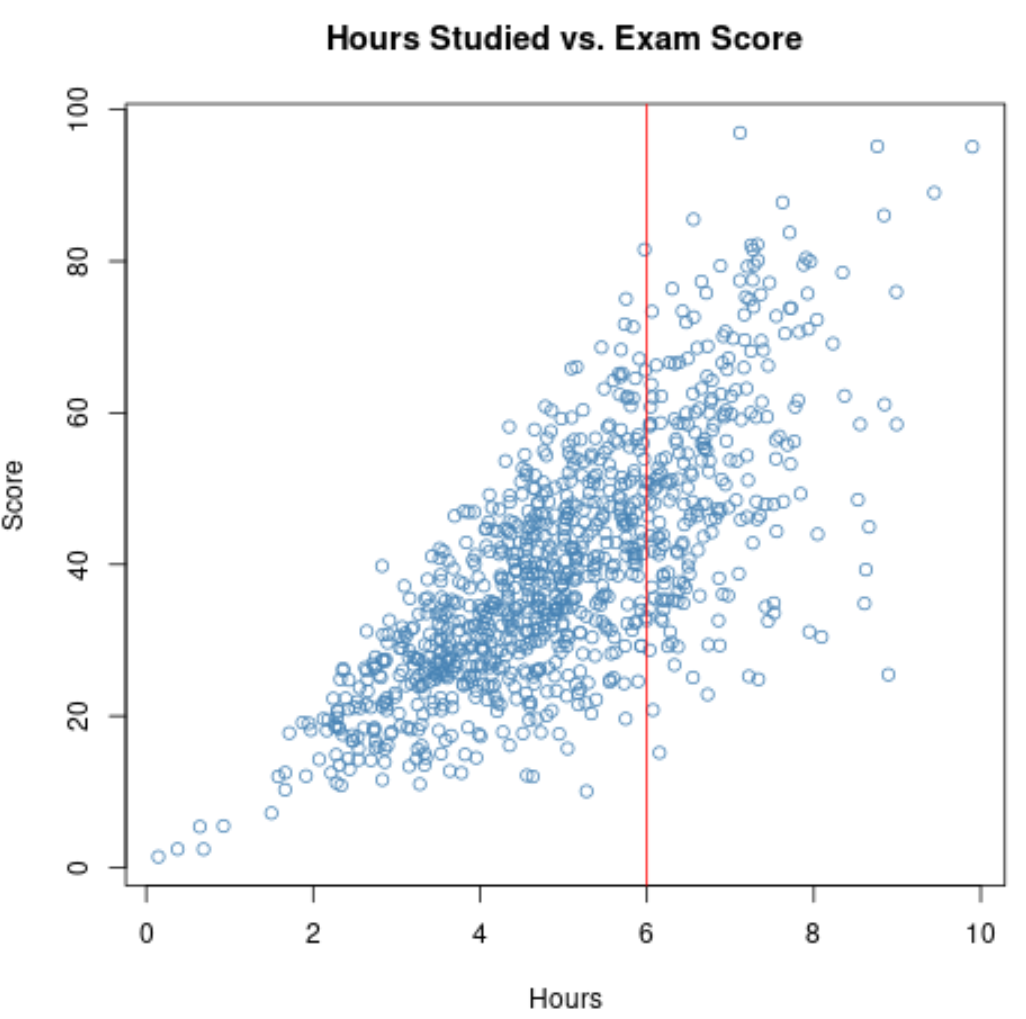
Saatlerin 6’dan büyük olduğu aralık için dağılım grafiğini yakınlaştırırsak, grafik şöyle görünür:

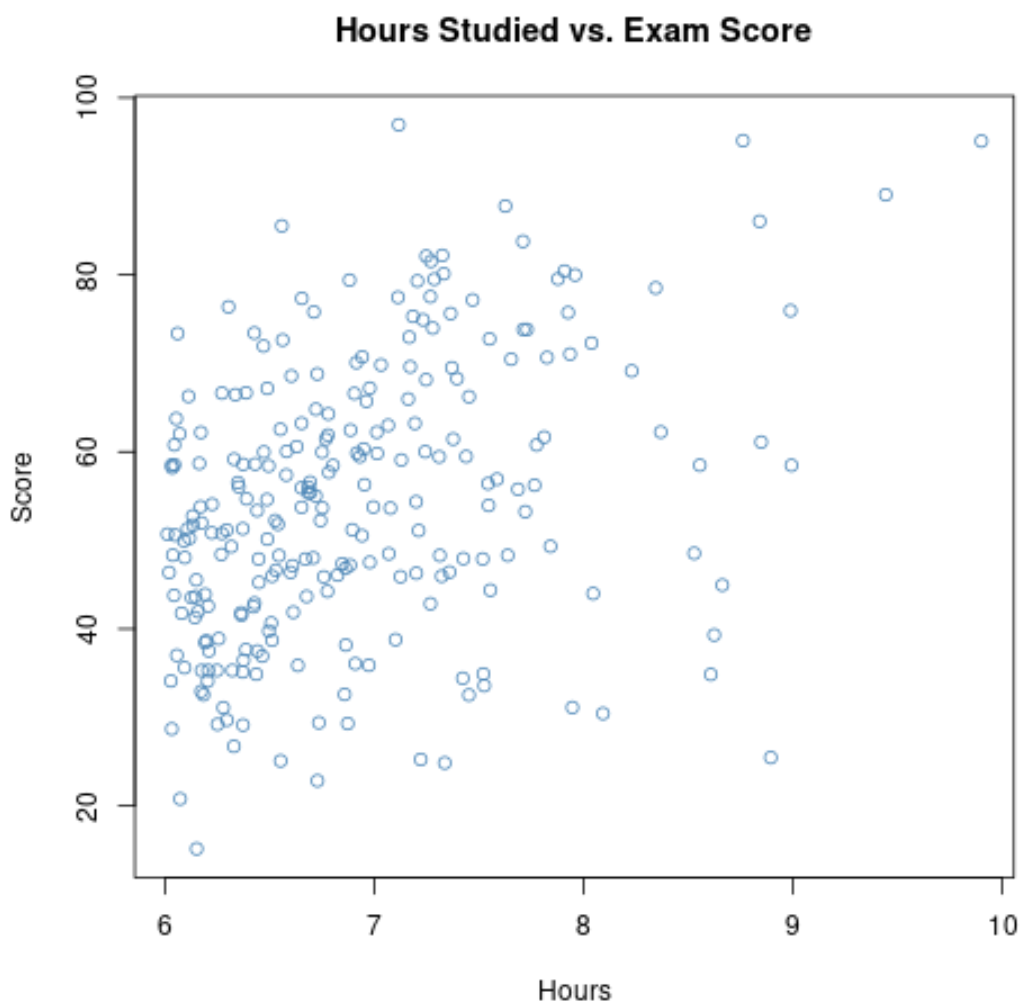
Bu grafikte iki değişken arasındaki korelasyon 0,37 olarak ortaya çıkıyor ve bu da 0,73’ten oldukça düşük.

Bu nedenle, üstün nitelikli derslerde okuyan öğrencilerin yalnızca ders çalışma saatleri ve sınav puanları hakkında veri toplasaydık, çalışılan saatler ile sınav puanları arasında zayıf bir ilişki olduğunu varsayabiliriz.

Ancak değişkenlerden biri için kısıtlı bir aralık kullandığımızdan bu sonuç yanıltıcı olacaktır.

Kısıtlı aralığın gerçek dünyadan örnekleri

Sınırlı aralık sorunu pratikte birçok farklı araştırma çalışmasında ortaya çıkabilir. İşte bazı örnekler:

1. Yüksek performanslı sporcular üzerinde yapılan çalışmalar . Araştırmacılar, belirli bir antrenman programının belirli bir standart programdan daha fazla kas kütlesi üretip üretmediğini araştırmakla ilgilenebilir.

Eğer araştırmacılar yalnızca elit sporcular hakkında veri topluyorsa, bu sporcuların hepsinin zaten yüksek kas kütlesine sahip olması muhtemeldir. Bu nedenle, antrenman programı ile üretilen kas kütlesi arasındaki korelasyonu hesaplamak için dar bir değer aralığı olacaktır.

2. Yüksek başarılı öğrencilerle ilgili çalışmalar. Araştırmacılar belirli bir özel ders programının notlar üzerinde olumlu bir etkisi olup olmadığını araştırmak isteyebilirler. Doğası gereği notlarını yükseltmeye ve özel ders programına katılmaya istekli öğrenciler zaten yüksek başarılı öğrenciler olabilir.

Dolayısıyla bu öğrencilerin notlarında iyileştirmeye pek yer kalmayabilir. Araştırmacılar özel ders programında harcanan saat ile bunun sonucunda ortaya çıkan not artışı arasındaki ilişkiyi hesaplarken, not iyileştirme alanı kısıtlı olduğundan gerçek korelasyon hafife alınabilir.

Kısıtlı aralıklar nasıl hesaba katılır?

Kısıtlı aralıkları açıklamanın popüler bir yolu, psikometrist Robert L. Thorndike tarafından geliştirilen bir formül olan Thorndike Vakası 2 olarak bilinir.

Bu formül, iki değişken arasındaki gerçek korelasyona ilişkin bir tahmin sağlar ve aşağıdaki hesaplamayı kullanır:

Doğru korelasyon = √(1-(SD ² _{y kısıtlı} -SD ² _{y sınırsız} )) * (1-r ² _kısıtlı )

Altın:

• SD ² _{sınırlı y} : Yanıt değişkeni y’ye ilişkin mevcut verilerin standart sapmasının karesi.
• _{Kısıtlanmamış} SD ² y: Popülasyon için yanıt değişkeninin bilinen kare standart sapması.
• r ² _kısıtlı : Mevcut kısıtlı veriler üzerindeki ikinci dereceden korelasyon.

Bu formülün, değişkenlerden biri sınırlı bir aralığa sahip olduğunda, iki değişken arasındaki gerçek korelasyona ilişkin tarafsız tahminler üretmede etkili olduğu gösterilmiştir.

Bu formülü kullanmak için yanıt değişkenine ilişkin gerçek popülasyon standart sapmasına ilişkin bir tahmine sahip olmanız gerektiğini unutmayın.