Aritmetik ortalama

İle Dr.benjamin anderson Ağustos 6, 2023 İstatistik 0 Yorum

Burada aritmetik ortalamanın ne olduğunu ve nasıl hesaplandığını açıklıyoruz. Herhangi bir istatistiksel örneğin aritmetik ortalamasını bulmak için aritmetik ortalama örnekleri ve hatta bir hesap makinesi bulacaksınız. Son olarak bu tür ortalamanın özelliklerinin neler olduğunu ve aralıklara göre gruplandırılmış verilerle aritmetik ortalamanın nasıl elde edildiğini görebileceksiniz.

Aritmetik ortalama nedir?

Aritmetik ortalama, bir dizi istatistiksel verinin merkezi değer özelliğidir. Aritmetik ortalamayı hesaplamak için tüm değerler toplanır ve toplam veri sayısına bölünür.

Ayrıca aritmetik ortalama, bir numunenin istatistiksel çalışmasını yürütmek için kullanılan ana göstergelerden biridir.

Dolayısıyla aritmetik ortalamanın formülü aşağıdaki gibidir:

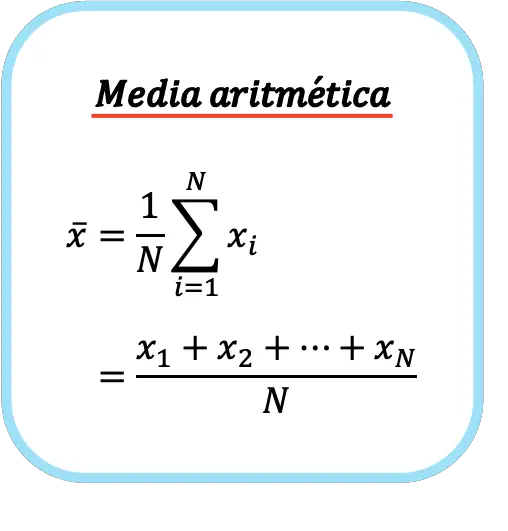
Aritmetik ortalamanın sembolü x harfinin üzerinde yatay bir banttır.

$(\overline{x}).$

Ayrıca ortalama simgesiyle örnek ortalamasını popülasyon ortalamasından ayırt edebilirsiniz: bir örneğin ortalaması simgesiyle ifade edilir.

$\overline{x}$

, bir nüfusun ortalaması için ise Yunan harfini kullanıyoruz.

$\mu.$

Bir popülasyonun aritmetik ortalamasının istatistiksel değişkenin beklenen değerine eşdeğer olduğuna dikkat edilmelidir.

Aritmetik ortalama olarak da adlandırılan aritmetik ortalama, var olan tek ortalama türü değildir; diğerlerinin yanı sıra ağırlıklı ortalama, kare ortalama, geometrik ortalama ve harmonik ortalama da vardır. Web sitemizin arama motorunda her birinin nasıl hesaplandığını görebilirsiniz.

Aritmetik ortalama nasıl hesaplanır

Aritmetik ortalamayı hesaplamak için aşağıdaki adımlar gerçekleştirilmelidir:

Örnekteki tüm istatistiksel verileri ekleyin.
Önceki toplamı toplam veri sayısına bölün.
Elde edilen sonuç istatistiksel örneğin aritmetik ortalamasıdır.

👉Herhangi bir veri setinin aritmetik ortalamasını hesaplamak için aşağıdaki hesap makinesini kullanabilirsiniz.

Aritmetik ortalamayı hesaplama örneği

Aritmetik ortalamanın tanımı göz önüne alındığında, adım adım bir örnek çözerek bir veri kümesinin aritmetik ortalamasının nasıl elde edileceğini göreceğiz.

Bir öğrenci bir okul yılı boyunca şu notları aldı: matematikte 9, dilde 7, tarihte 6, ekonomide 8 ve fen bilimlerinde 7,5. Tüm notlarınızın aritmetik ortalaması nedir?

Aritmetik ortalamayı bulmak için tüm notları toplayıp dersteki toplam ders sayısına (5) bölmemiz gerekir. Bu nedenle aritmetik ortalama formülünü uygularız:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+x_3+x_4+x_5}{N}$

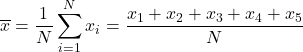
Verileri formülde yerine koyarız ve aritmetik ortalamayı hesaplarız:

$\overline{x}=\cfrac{9+7+5+8+7,5}{5}=7,3$

Gördüğünüz gibi aritmetik ortalamada her değere aynı ağırlık atanır, yani her veri parçası bütün içinde aynı ağırlığa sahiptir.

Aritmetik Ortalama Hesaplayıcı

Aritmetik ortalamasını hesaplamak için herhangi bir istatistiksel örnekten verileri aşağıdaki hesap makinesine girin. Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.

Gruplandırılmış veriler için aritmetik ortalama

Gruplandırılmış verilerle, verilerin gruplar veya aralıklar halinde yapılandırılmasını kastediyoruz. Bu genellikle istatistiksel örneklem büyüklüğü çok büyük olduğunda meydana gelir.

Dolayısıyla, kavram aynı olsa bile, veriler bir arada gruplandığında aritmetik ortalamanın hesaplanması biraz farklılık gösterir.

Aralıklara göre gruplandırılmış verilerin aritmetik ortalamasını hesaplamak için, her grubun sınıf puanı mutlak frekansıyla çarpılmalı ve ardından tüm mutlak frekansların toplamına bölünmelidir.

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{x_1\cdot f_1+ x_2\cdot f_2+\dots +x_N\cdot f_N}{N}$

Not: Bir aralığın sınıf puanı, aralığın uç noktalarının toplamının ikiye bölünmesiyle hesaplanır. Örneğin, [3,7) aralığının sınıf notu şöyle olacaktır:

$\cfrac{3+7}{2}=5$

Bunun nasıl yapıldığını görebilmeniz için aşağıda aralıklara göre gruplandırılmış verilerin aritmetik ortalamasına ilişkin çözülmüş bir alıştırma bulunmaktadır:

Bir grubun ağırlığını istatistiksel olarak incelemek istiyoruz, bunun için 81 kişilik temsili bir grupla görüştük ve aşağıdaki verileri elde ettik:

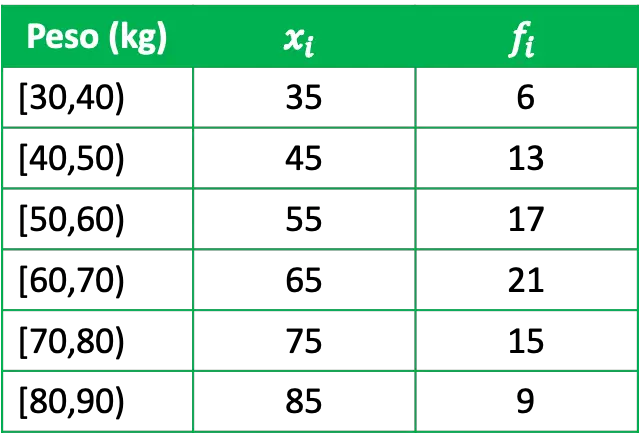
Burada x _i her grubun sınıf puanı ve f _i mutlak frekansı, yani bu aralıkta ağırlığı olan kişi sayısıdır.

Aritmetik ortalamayı belirlemek için, ders notlarının ilgili mutlak frekanslarına göre çarpımı olan frekans tablosuna bir sütun eklemek gerekir:

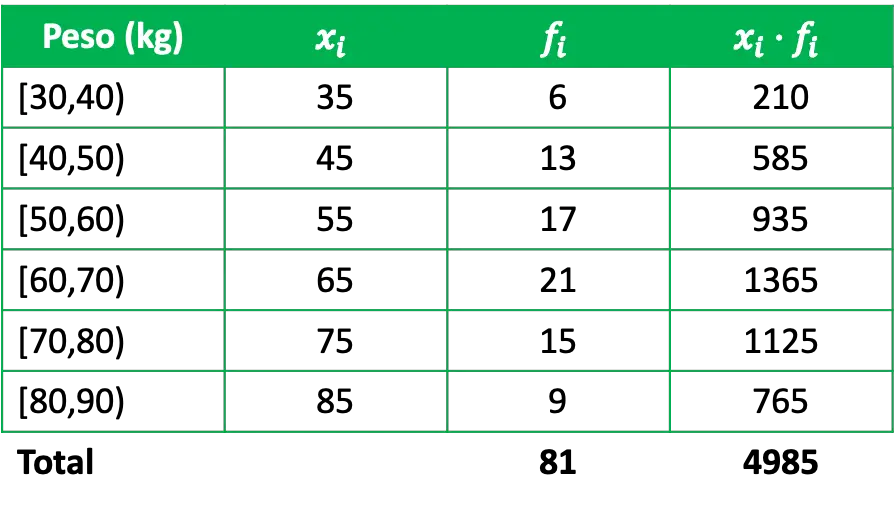
gruplandırılmış veriler için çözülmüş aritmetik ortalama alıştırması

Böylece, gruplandırılmış verilerin aritmetik ortalamasını hesaplamak için, ders notlarının çarpımlarının toplamını, frekanslarına göre toplam veri sayısına bölmeniz yeterlidir:

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{4985}{81}=61,54 \text{ kg}$

Aritmetik ortalamanın özellikleri

Aritmetik ortalama aşağıdaki özelliklere sahiptir:

Bir dağılımdaki tüm verilerin ortalamadan sapmalarının toplamı sıfırla sonuçlanır.

$\sum_{i=1}^N\left(x_i-\overline{x}\right)=0$

Bir örneklemdeki tüm verilere aynı miktarı eklersek örneklem ortalaması o kadar artar.

Çarpma işleminde de aynı şey olur, bir örnekteki tüm değerler bir sayıyla çarpılırsa örnek ortalaması o sayıyla çarpılır.

Aritmetik ortalama yalnızca niceliksel değişkenlerde hesaplanabilir. Başka bir deyişle niteliksel değişkenlerin ortalamasını alamazsınız.

Aritmetik ortalama her zaman bir dağılımın minimum ve maksimum değerleri arasında bir değer olacaktır.

$\text{min}\{x_1,x_2,...,x_N\}\leq \cfrac{x_1+\dots +x_N}{N}\leq \text{max}\{x_1,x_2,...,x_N\}$

Bu tür ortalama, çok yüksek veya çok düşük değerlere karşı çok hassastır ve aykırı değerin aritmetik ortalamanın sonucunu önemli ölçüde değiştirmesine neden olur.

Bir veri kümesinin aritmetik ortalaması her zaman aynı veri kümesinin geometrik ortalamasına eşit veya ondan daha büyüktür.

$\displaystyle\frac{x_1+x_2+\dots+x_N}{N}\geq \sqrt[N]{x_1+x_2+\dots+x_N}$

Aritmetik ortalamayı Excel ile hesaplayın

Excel’de aritmetik ortalamayı hesaplamak çok basittir, çünkü verileri bir sayfaya girmeniz ve ORTALAMA işlevini kullanmanız yeterlidir.

Örneğin, açıkladığımız ilk çözülmüş alıştırmadaki verilerin aritmetik ortalamasını belirlemek için, tüm verileri bir Excel belgesine kopyalayıp bir hücreye aşağıdaki formülü yazmanız yeterlidir: =ORTALAMA(9;7;5; 8;7) ,5) . İşlev, verilerin aritmetik ortalamasını (7,3) döndürür.

Açıkçası, belirli sayıların aritmetik ortalamasını Excel programıyla bulmak, özellikle örneklem boyutu çok büyük olduğunda, elle hesaplamaktan çok daha hızlıdır.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil