İkincil olasılık: tanım + örnek

A posteriori olasılık, yeni bilgiler dikkate alındıktan sonra bir olayın meydana gelme ihtimalinin güncellenmiş halidir.

Örneğin, yeni meydana gelen bir “B” olayının muhasebeleştirilmesinden sonra “A” olayının meydana gelme olasılığı ilgimizi çekebilir. Bu sonsal olasılığı aşağıdaki formülü kullanarak hesaplayabiliriz:

P(A|B) = P(A) * P(B|A) / P(B)

Altın:

P(A|B) = B olayının meydana geldiği göz önüne alındığında, A olayının meydana gelme olasılığı. “| » “verilen” anlamına gelir.

P(A) = A olayının meydana gelme olasılığı.

P(B) = B olayının meydana gelme olasılığı.

P(B|A) = A olayının meydana geldiği göz önüne alındığında, B olayının meydana gelme olasılığı.

Örnek: Son olasılığın hesaplanması

Bir ormanın %20’si meşe, %80’i akçaağaçlardan oluşur. Meşe ağaçlarının %90’ının sağlıklı, akçaağaçların ise yalnızca %50’sinin sağlıklı olduğunu bildiğimizi varsayalım. Belirli bir ağacın sağlıklı olduğunu uzaktan söyleyebildiğinizi varsayalım. Ağacın meşe olma olasılığı nedir?

B olayının meydana geldiği dikkate alındığında A olayının meydana gelme olasılığının şöyle olduğunu hatırlayın:

P(A|B) = P(A) * P(B|A) / P(B)

Bu örnekte ağacın sağlıklı olması durumunda ağacın meşe olma olasılığı:

P(Meşe|Sağlıklı) = P(Meşe) * P(Sağlıklı|Meşe) / P(Sağlıklı)

P(Meşe) = Belirli bir ağacın meşe olma olasılığı 0,2’dir çünkü ormandaki tüm ağaçların %20’si meşedir.

P(Sağlıklı) = Belirli bir ağacın sağlıklı olma olasılığı şu şekilde hesaplanabilir: (0,20)*(0,9) + (0,8)*(0,5) = 0,58 .

P(Sağlıklı|Meşe) = Bir ağacın meşe olduğu dikkate alındığında sağlıklı olma olasılığı 0,9’dur , çünkü bize meşelerin %90’ının sağlıklı olduğu söylenmiştir.

Bu üç sayıyı kullanarak ağacın sağlıklı olması koşuluyla meşe olma olasılığını bulabiliriz:

P(Meşe|Sağlıklı) = P(Meşe) * P(Sağlıklı|Meşe) / P(Sağlıklı) = (0,2) * (0,9) / (0,58) = 0,3103 .

Bu olasılığın sezgisel olarak anlaşılması için aşağıdaki tablonun 100 ağaçtan oluşan bu ormanı temsil ettiğini varsayalım. Ağaçların tam 20’si meşe, 18’i sağlıklı. Diğer 80 ağaç ise akçaağaç olup 40 tanesi sağlıklıdır.

(O = Meşe, M = Akçaağaç, Yeşil = Sağlıklı, Kırmızı = Sağlıksız)

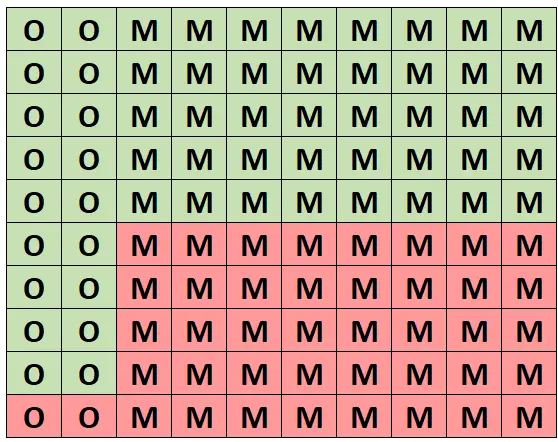
Tüm ağaçların tam olarak 58’i sağlıklı ve bu sağlıklı ağaçların 18’i meşedir. Yani sağlıklı bir ağaç seçtiğimizi biliyorsak, bunun meşe olma olasılığı 18/58 = 0,3103’tür .

Posterior olasılığı ne zaman kullanmalısınız?

Arka olasılık, finans, tıp, ekonomi ve hava tahmini dahil olmak üzere çok çeşitli alanlarda kullanılmaktadır.

Sonsal olasılıkları kullanmanın amacı, yeni bir bilgi elde ettiğimizde bir şey hakkında sahip olduğumuz önceki inancımızı güncellemektir.

Önceki örnekten ormandaki belirli bir ağacın meşe olma olasılığının %20 olduğunu bildiğimizi hatırlayın. Buna ön olasılık denir. Eğer rastgele bir ağaç seçseydik, onun meşe olma ihtimalinin 0,20 olduğunu biliyorduk.

Ancak, seçtiğimiz ağacın sağlıklı olduğuna dair yeni bilgiyi aldıktan sonra, bu yeni bilgiyi kullanarak bu ağacın meşe olma olasılığının 0,3103 olduğunu belirleyebildik.

Gerçek dünyada insanlar sürekli olarak yeni bilgiler keşfediyorlar. Bu yeni bilgi önceki inançlarımızı güncellememize yardımcı olur. İstatistiksel açıdan bu, meydana gelen olayların arka olasılıklarını üretebildiğimiz anlamına gelir; bu da dünyayı daha doğru bir şekilde anlamamıza yardımcı olur ve gelecekteki olaylar hakkında daha doğru tahminler yapmamıza olanak tanır.