Kalan boşluk nedir? (tanım & #038; örnek)

Artık varyans (bazen “açıklanamayan varyans” olarak da adlandırılır), bir modeldeki model değişkenleri tarafından açıklanamayan varyansı ifade eder.

Bir modelin artık varyansı ne kadar yüksek olursa, model verilerdeki değişimi o kadar az açıklayabilir.

İki farklı istatistiksel modelin sonuçlarında artık varyans ortaya çıkıyor:

1. ANOVA: üç veya daha fazla bağımsız grubun ortalamalarını karşılaştırmak için kullanılır.

2. Regresyon: Bir veya daha fazla öngörücü değişken ile bir yanıt değişkeni arasındaki ilişkiyi ölçmek için kullanılır.

Aşağıdaki örnekler, bu yöntemlerin her birindeki artık varyansın nasıl yorumlanacağını göstermektedir.

ANOVA modellerinde kalan varyans

Bir ANOVA (“varyans analizi”) modelini her yerleştirdiğimizde, aşağıdakine benzeyen bir ANOVA tablosu elde ederiz:

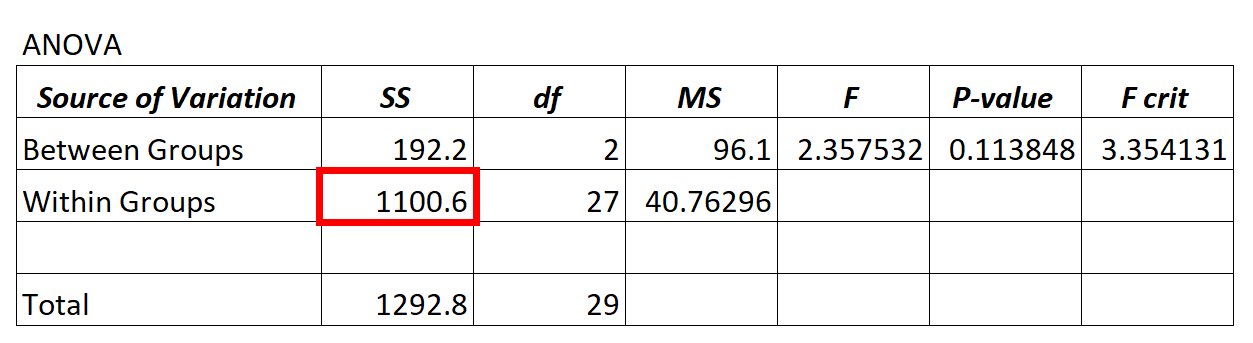
ANOVA modelinden kalan varyans değeri , grup içi varyasyon için SS (“kareler toplamı”) sütununda bulunur.

Bu değer aynı zamanda “hataların karelerinin toplamı” olarak da adlandırılır ve aşağıdaki formül kullanılarak hesaplanır:

Σ(X _ij – X _j ) ²

Altın:

• Σ : “toplam” anlamına gelen Yunanca bir sembol
• X _ij : j grubunun ^i’inci gözlemi
• X _j : j grubunun ortalaması

Yukarıdaki ANOVA modelinde artık varyansın 1100,6 olduğunu görüyoruz.

Bu artık varyansın “yüksek” olup olmadığını belirlemek için, gruplar içindeki ortalama kareler toplamını ve gruplar arasındaki ortalama kareler toplamını hesaplayabilir ve ikisi arasındaki oranı bulabiliriz; bu, ANOVA tablosundaki genel F değerini verir.

• F = MS _girer / MS _girer
• F = 96,1 / 40,76296
• F = 2,357

Yukarıdaki ANOVA tablosunda F değeri 2,357 ve buna karşılık gelen p değeri 0,113848’dir. Bu p değeri α = 0,05’ten küçük olmadığından sıfır hipotezini reddetmek için yeterli kanıtımız yok.

Bu, karşılaştırdığımız gruplar arasındaki ortalama farkın önemli ölçüde farklı olduğunu söylemek için yeterli kanıta sahip olmadığımız anlamına geliyor.

Bu bize ANOVA modelinin artık varyansının, modelin gerçekte açıklayabildiği varyasyonla karşılaştırıldığında yüksek olduğunu söyler.

Regresyon modellerinde kalan varyans

Bir regresyon modelinde artık varyans, tahmin edilen veri noktaları ile gözlemlenen veri noktaları arasındaki farkların karelerinin toplamı olarak tanımlanır.

Aşağıdaki şekilde hesaplanır:

Σ(ŷ _ben – y _ben ) ²

Altın:

• Σ : “toplam” anlamına gelen Yunanca bir sembol
• ŷ _i : Tahmin edilen veri noktaları
• y _i : Gözlemlenen veri noktaları

Bir regresyon modelini uydurduğumuzda genellikle aşağıdakine benzer bir sonuç elde ederiz:

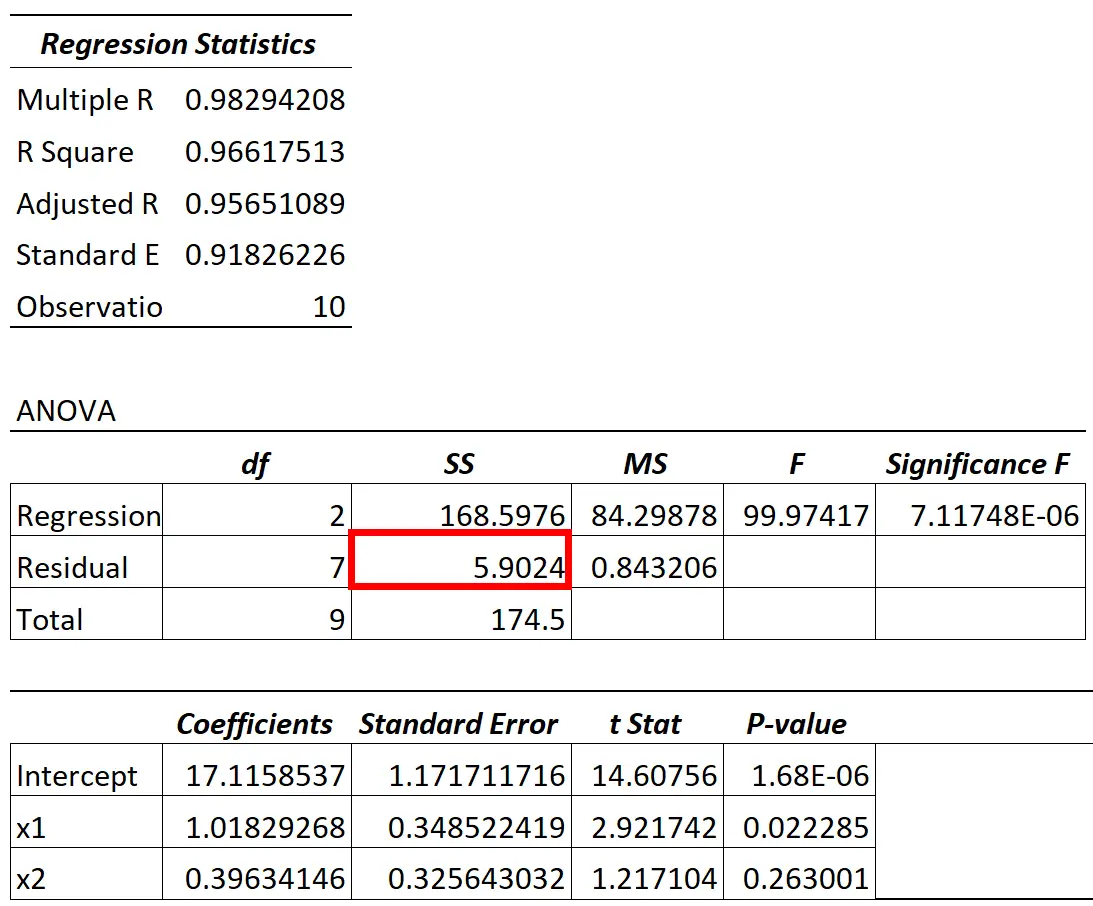
ANOVA modelinden elde edilen artık varyans değeri, artık varyasyon için SS (“kareler toplamı”) sütununda bulunabilir.

Modeldeki artık varyasyonun toplam varyasyona oranı bize, yanıt değişkenindeki, modeldeki yordayıcı değişkenler tarafından açıklanamayan varyasyonun yüzdesini anlatır.

Örneğin yukarıdaki tabloda bu yüzdeyi şu şekilde hesaplayabiliriz:

• Açıklanamayan değişim = SS Artık / SS Toplamı
• Açıklanamayan varyasyon = 5,9024 / 174,5
• Açıklanamayan varyasyon = 0,0338

Bu değer aşağıdaki formül kullanılarak da hesaplanabilir:

• Açıklanamayan varyasyon = 1 – R ²
• Açıklanamayan varyasyon = 1 – 0,96617
• Açıklanamayan varyasyon = 0,0338

Modelin R-kare değeri bize, yordayıcı değişken tarafından açıklanabilecek yanıt değişkenindeki varyasyonun yüzdesini verir.

Dolayısıyla, açıklanamayan varyasyon ne kadar düşük olursa, bir model, yanıt değişkenindeki varyasyonu açıklamak için yordayıcı değişkenleri kullanma konusunda o kadar yetenekli olur.

Ek kaynaklar

İyi bir R-kare değeri nedir?
Excel’de R-kare nasıl hesaplanır
R’de R-kare nasıl hesaplanır