Asimetri türleri

İle Dr.benjamin anderson Ağustos 5, 2023 İstatistik 0 Yorum

Bu yazıda istatistikte kaç tür asimetrinin bulunduğunu öğreneceksiniz. Böylece her asimetri türü örneklerle açıklanacak ve ayrıca bir dağılımın asimetrisinin nasıl hesaplandığını görebileceksiniz.

Asimetri türleri nelerdir?

İstatistikte üç tür asimetri vardır:

Pozitif çarpıklık : Dağılımın ortalamanın sağında, solunda olduğundan daha farklı değerleri vardır.
Negatif çarpıklık : Dağılımın ortalamanın solunda sağına göre daha farklı değerleri vardır.
Simetri : Dağılım, ortalamanın solunda ve sağında aynı sayıda değere sahiptir.

Her asimetri türü aşağıda daha ayrıntılı olarak açıklanmaktadır.

pozitif asimetri

Bir dağılımın pozitif çarpıklığı varsa, bu, grafiğin sağ kuyruğunun sol kuyruktan daha uzun olduğu anlamına gelir. Yani dağılım ortalamanın sağında daha farklı değerlere sahiptir.

Önceki örnekteki eğri pozitif asimetriktir çünkü ortalamanın sağında sola göre çok daha fazla değer vardır. Grafikten görebileceğiniz gibi yeşil renkle gösterilen çubuk, turuncu çubuktan çok daha büyüktür.

negatif asimetri

İstatistiklerde, grafiğinin sol kuyruğu sağ kuyruktan daha uzun olduğunda, bir dağılımın negatif çarpık olduğu söylenir. Yani negatif çarpık bir dağılım, ortalamanın solunda daha farklı değerlere sahip olduğu anlamına gelir.

Önceki grafiğe bakarsanız ortalamanın solunda sağa göre daha fazla değer var, dolayısıyla eğri negatif çarpık.

Simetri

Ortalamanın solundaki değerlerin sayısı, ortalamanın sağındaki değerlerin sayısına eşit olduğunda dağılım simetriktir . Bu nedenle ortalama bir simetri ekseni görevi görür.

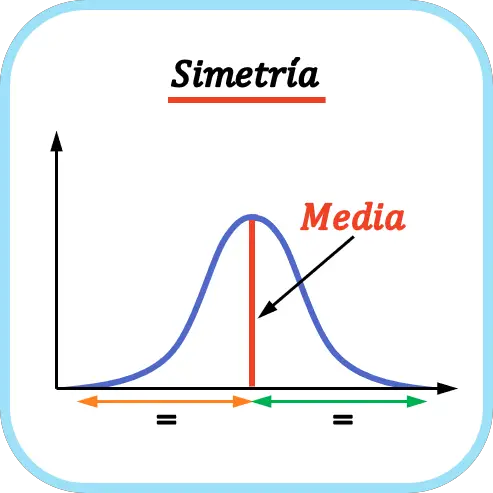
Yukarıdaki örnekte gösterildiği gibi, temsil edilen olasılık dağılımının ortalamasının solundaki değer sayısı, ortalamanın sağındaki değer sayısıyla çakışmaktadır, dolayısıyla simetrik bir dağılımdır.

Asimetri türü nasıl belirlenir

Artık istatistikte farklı asimetri türlerinin ne olduğunu bildiğimize göre, bir olasılık dağılımının ne tür asimetriye karşılık geldiğini nasıl bileceğimizi görelim.

Geleneksel olarak, bir dağılımın çarpıklığının türünü, ortalaması ile medyanı arasındaki ilişkiye (daha büyük, eşdeğer veya daha küçük olup olmadığına) dayanarak bilebileceğimiz açıklanır. Ancak bu özellik her zaman tatmin edici değildir. Bu nedenle bir dağılımın çarpıklığını belirlemek için Fisher’in çarpıklık katsayısının hesaplanması gerekir.

Fisher asimetri katsayısı aşağıdaki formül kullanılarak hesaplanır:

$\displaystyle\gamma_1=E\left[\left(\frac{X-\mu}{\sigma}\right)^3 \right]$

Veya eşdeğer:

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\mu\sigma^2 - \mu^3}{\sigma^3}$

Altın

$E$

matematiksel beklenti ,

$\mu$

aritmetik ortalama ve

$\sigma$

standart sapma .

Fisher katsayısı hesaplandıktan sonra işareti, dağılımın ne tür bir asimetri sunduğunu belirlemeyi mümkün kılar:

Fisher’in çarpıklık katsayısı pozitif ise dağılım pozitif çarpıktır.
Fisher’in çarpıklık katsayısı negatif ise dağılım negatif çarpıktır.
Dağılım simetrikse Fisher’in çarpıklık katsayısı sıfıra eşittir (tersi her zaman doğru değildir).

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil