Ayrık düzgün dağılım

İle Dr.benjamin anderson Ağustos 3, 2023 Olasılık 0 Yorum

Bu makale ayrık düzgün dağılımın ne olduğunu ve karakteristik formülünün ne olduğunu açıklamaktadır. Aynı şekilde ayrık düzgün dağılımın grafiksel gösterimini ve özelliklerinin neler olduğunu görebileceksiniz.

Ayrık düzgün dağılım nedir?

Ayrık tekdüze dağılım, tüm değerlerin eş olasılıklı olduğu, yani ayrık bir tekdüze dağılımda tüm değerlerin aynı oluşma olasılığına sahip olduğu ayrı bir olasılık dağılımıdır.

Örneğin, tüm olası sonuçların (1, 2, 3, 4, 5 veya 6) aynı oluşma olasılığına sahip olması nedeniyle, bir zarın atılması ayrık ve düzgün bir dağılımla tanımlanabilir.

Genel olarak, ayrık bir düzgün dağılım, dağılımın alabileceği olası değerlerin aralığını tanımlayan a ve b olmak üzere iki karakteristik parametreye sahiptir. Bu nedenle, bir değişken ayrık bir düzgün dağılımla tanımlandığında, Düzgün(a,b) olarak yazılır.

Ayrık tekdüze dağılım, rastgele deneyleri tanımlamak için kullanılabilir çünkü tüm sonuçların aynı olasılığa sahip olması, deneyin rastgele olduğu anlamına gelir.

Ayrık düzgün dağılım formülü

Artık ayrık düzgün dağılımın tanımını bildiğimize göre, bu tür bir dağılımın değerlerinin ortaya çıkma olasılığını hesaplamamızı sağlayan formülün ne olduğunu göreceğiz.

Ayrık bir düzgün dağılımın olasılık fonksiyonu sabittir ve değeri, olası sonuçların toplam sayısı üzerinden bire eşittir. Dolayısıyla ayrık düzgün dağılım formülü aşağıdaki gibidir:

$P[X=x]=\cfrac{1}{n}=\cfrac{1}{b-a+1}$

Öte yandan ayrık düzgün dağılımın kümülatif olasılık fonksiyonunun formülü aşağıdaki gibidir:

$P[X\leq x]=\cfrac{\lfloor x \rfloor -a + 1}{b-a+1}$

Altın

$a$

$b$

ayrık düzgün dağılımın karakteristik parametreleridir.

Ayrık düzgün dağıtım diyagramı

Ayrık düzgün dağılım bir aralıkta yalnızca belirli değerleri alabildiğinden grafiksel gösterimi noktalardan oluşur. Ayrıca, tüm olasılıklar eşittir, dolayısıyla ayrık düzgün dağılımdaki tüm noktalar aynı dikey koordinata sahiptir.

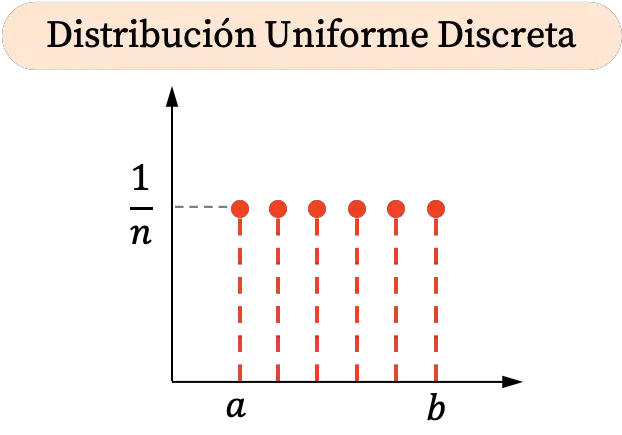
Öte yandan ayrık düzgün dağılımın kümülatif olasılık grafiği şu şekildedir:

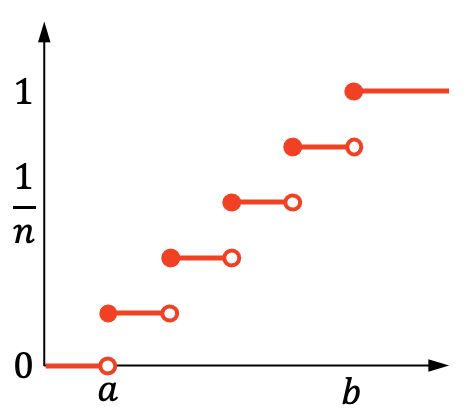
ayrık düzgün dağılımın kümülatif olasılığı

Ayrık düzgün dağılımın özellikleri

Ayrık düzgün dağılım aşağıdaki özelliklere sahiptir:

Ayrık düzgün dağılım, dağılımın olası değerlerinin aralığını belirleyen a ve b olmak üzere iki tamsayı parametresi ile tanımlanır.

$\begin{array}{c} X\sim \text{Uniforme}(a,b)\\[2ex]b\geq a\\[2ex]n=b-a+1\end{array}$

Ayrık bir düzgün dağılımın ortalaması, iki karakteristik parametresinin toplamının ikiye bölünmesine eşittir.

$E[X]=\cfrac{a+b}{2}$

Ayrık bir düzgün dağılımın medyanı, ortalamasına eşdeğerdir, dolayısıyla aynı ifadeyle hesaplanır:

$Me=\cfrac{a+b}{2}$

Ayrık bir düzgün dağılımın varyansı, toplam sonuç sayısının karesinden eksi bir bölü on ikiye eşittir.

$Var(X)=\cfrac{n^2-1}{12}$

Ayrık düzgün dağılım, ortalamasına göre simetriktir, dolayısıyla bu olasılık dağılımının çarpıklık katsayısı sıfırdır.

$A=0$

Ayrık düzgün dağılımın basıklığı aşağıdaki ifade kullanılarak hesaplanabilir:

$C=-\cfrac{6\cdot (n^2+1)}{5\cdot (n^2+1)}$

Ayrık düzgün dağılım ve sürekli düzgün dağılım

Son olarak, ayrık bir düzgün dağılım ile sürekli bir tekdüze dağılım arasındaki farkın ne olduğunu göreceğiz, çünkü bunlar iki benzer tür olasılık dağılımıdır, ancak önemli bir fark vardır.

Ayrık bir düzgün dağılım ile sürekli bir tekdüze dağılım arasındaki fark, bunların olası değerlerinde yatmaktadır. Ayrık düzgün dağılım bir aralıkta yalnızca belirli değerleri alabilirken, sürekli düzgün dağılım tanımlandığı aralıktaki herhangi bir değeri alabilir.

Genel olarak, ayrık tekdüze dağılımlar yalnızca tam sayı değerleri alabilirken, sürekli tekdüze dağılımlar da ondalık değerler alabilir.

➤ Bakınız: Sürekli düzgün dağılım

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil