Göreceli risk için güven aralığı nasıl hesaplanır?

Göreceli risk genellikle aşağıdaki formatı alan 2×2’lik bir tablo analiz edilirken hesaplanır:

Göreceli risk, bir olayın kontrol grubunda meydana gelme olasılığına kıyasla tedavi grubunda meydana gelen bir olayın olasılığını belirtir.

Aşağıdaki şekilde hesaplanır:

• Göreceli risk = [A/(A+B)] / [C/(C+D)]

Daha sonra bağıl risk (RR) için bir güven aralığı hesaplamak amacıyla aşağıdaki formülü kullanabiliriz:

• CI %95’ten az = e ^{ln(RR) – 1,96√ 1/a + 1/c – 1/(a+b) – 1/(c+d)}
• CI %95’ten büyük = e ^{ln(RR) + 1,96√ 1/a + 1/c – 1/(a+b) – 1/(c+d)}

Aşağıdaki örnek, göreceli riskin ve buna karşılık gelen güven aralığının pratikte nasıl hesaplanacağını göstermektedir.

Örnek: Göreceli risk için güven aralığının hesaplanması

Bir basketbol antrenörünün, eski bir antrenman programına kıyasla belirli bir beceri testini geçebilecek oyuncu sayısını artırıp artırmadığını görmek için yeni bir antrenman programı kullandığını varsayalım.

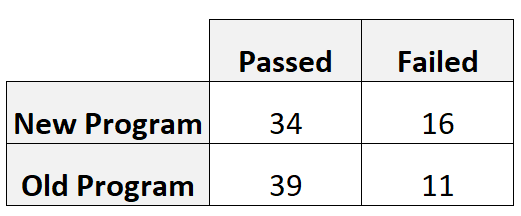
Koç, her programı kullanmak için 50 oyuncuyu işe alır. Aşağıdaki tablo, kullandıkları programa göre beceri testini geçen ve başarısız olan oyuncuların sayısını göstermektedir:

Göreceli riski şu şekilde hesaplayabiliriz:

• Göreceli risk = [A/(A+B)] / [C/(C+D)]
• Göreceli risk = [34/(34+16)] / [39/(39+11)]
• Göreceli risk = 0,8718

Bunu, bir oyuncunun yeni programı kullanarak testi geçme olasılığının, bir oyuncunun eski programı kullanarak testi geçme olasılığının yalnızca 0,8718 katı olduğu şeklinde yorumluyoruz.

Başka bir deyişle, yeni programın kullanılmasıyla aslında bir oyuncunun testi geçme olasılığı azaltılıyor.

Daha sonra göreceli risk için %95 güven aralığını hesaplamak üzere aşağıdaki formülleri kullanabiliriz:

• CI %95’ten az = e ^{ln(.8718) – 1,96√ (1/34 + 1/39 – 1/(34+16) – 1/(39+11)} = 0,686
• CI %95’ten büyük = e ^{ln(.8718) + 1.96√ (1/34 + 1/39 + 1/(34+16) – 1/(39+11)} = 1.109

Dolayısıyla göreceli risk için %95 güven aralığı [0,686, 1,109]’ dur.

Yeni ve eski eğitim programı arasındaki gerçek göreceli riskin bu aralıkta yer aldığından %95 eminiz.

Bu güven aralığı 1 değerini içerdiğinden istatistiksel olarak anlamlı değildir.

Aşağıdakileri göz önünde bulundurduğunuzda bu mantıklı olmalıdır:

• 1’den büyük bir göreceli risk, bir oyuncunun yeni programı kullanarak testi geçme olasılığının, bir oyuncunun testi geçme olasılığından daha yüksek olduğu anlamına gelir.
• 1’den küçük bir göreceli risk, bir oyuncunun yeni programı kullanarak testi geçme olasılığının, bir oyuncunun eski programı kullanarak testi geçme olasılığından daha az olduğu anlamına gelir.

Dolayısıyla, göreceli risk için %95 güven aralığımız 1 değerini içerdiğinden, bu, bir oyuncunun yeni programı kullanarak beceri testini geçme olasılığının, aynı oyuncunun yeni programı kullanarak testi geçme olasılığından daha büyük olabileceği veya olmayabileceği anlamına gelir. yeni program. eski program.

Ek kaynaklar

Aşağıdaki eğitimler olasılık oranları ve göreceli risk hakkında ek bilgi sağlar:

Oran oranları nasıl yorumlanır?
Göreceli risk nasıl yorumlanır?
Excel’de Oran Oranı ve Göreli Risk Nasıl Hesaplanır?