Bağımlı ve bağımsız değişken

Bu makalede bağımlı ve bağımsız değişkenlerin ne olduğu açıklanmaktadır. Böylece, bağımlı değişken ile bağımsız değişken arasındaki farkın ne olduğunu, hangisinin bağımlı değişken hangisinin bağımsız olduğunu nasıl bileceğinizi öğrenecek ve ayrıca bu tür değişkenlerin çeşitli örneklerini sunacaksınız.

Bağımlı ve bağımsız değişken nedir?

Bağımlı değişken, değeri bağımsız değişken olan başka bir değişkene bağlı olan değişkendir. Dolayısıyla bağımlı değişken ile bağımsız değişken arasındaki fark, bağımsız değişkenin başka bir değişkene bağlı olmaması, bağımlı değişkenin bağımsız değişkenin değerine bağlı olmasıdır.

Bir grafikte, bağımsız değişken apsis (yatay eksen) üzerinde x harfi ile temsil edilirken, bağımlı değişken ordinat (dikey eksen) üzerinde y harfi ile temsil edilir.

Örneğin istatistiksel bir çalışmada alınan not ile ayrılan ders saati arasındaki ilişkiyi analiz edersek, ayrılan ders saati bağımsız değişken, alınan not ise bağımlı değişkendir. Alınan not çalışılan saatlere bağlı olduğundan, tam tersi geçerli değildir.

Bağımlı ve Bağımsız Değişken Örnekleri

Önceki bölümde bağımlı ve bağımsız değişkenlerin tanımını görmüştük, şimdi anlamını daha iyi anlamak için bu tür değişkenlerin on örneğini göreceğiz.

1. Ders çalışmak için harcanan zaman (bağımsız değişken) alınan notları (bağımlı değişken) etkilemektedir.
2. Bir ürünün fiyatı (bağımsız değişken), ürünü satın almak isteyen kişi sayısını (bağımlı değişken) değiştirir.
3. Bir kişinin sağlığı (bağımlı değişken) beslenmesine (bağımsız değişken) bağlıdır.
4. Bir kişinin kalp atış hızı (bağımlı değişken), ne kadar yüksek olduğundan (bağımsız değişken) etkilenir.
5. Ortam sıcaklığı (bağımsız değişken) orman yangınlarının sayısını (bağımlı değişken) etkilemektedir.
6. Müşteri memnuniyeti düzeyi (bağımlı değişken), sunulan hizmetin kalitesine (bağımsız değişken) göre değişmektedir.
7. Bir ürünün reklamının yapılması (bağımsız değişken), söz konusu ürünün satış adedi (bağımlı değişken) üzerinde etkiye sahiptir.
8. Bir ülkenin saldığı kirletici maddelerin miktarı (bağımlı değişken) o ülkenin endüstriyel üretimine (bağımsız değişken) bağlıdır.
9. Bir taksi şoförünün maaşı (bağımlı değişken), yaptığı yolculuk sayısına (bağımsız değişken) bağlı olarak değişmektedir.
10. Bir şehrin sakinlerinin sayısı (bağımsız değişken), şehirdeki taksi sayısına (bağımlı değişken) bağlıdır.

Bir değişkenin bağlama bağlı olarak bağımlı veya bağımsız olduğunu unutmayın; çünkü araştırmaya bağlı olarak ilişkinin nedeni veya etkisi olarak hareket edecektir.

Bağımlı ve Bağımsız Değişkenler Alıştırmaları

Aşağıdaki durumlarda bağımlı değişken hangisi, bağımsız değişken hangisidir?

1. Bir şehrin sakin sayısı – Halk otobüsü sayısı
2. Aracın yaşı – Aracın durumu
3. Sivrisinek sayısı – Ortam sıcaklığı
4. Aydaki yağmurlu gün sayısı – Şemsiye talebi

1. Bağımlı değişken: Halk otobüsü sayısı – Bağımsız değişken: Bir şehrin sakinlerinin sayısı
2. Bağımlı değişken: Aracın durumu – Bağımsız değişken: Aracın yaşı
3. Bağımlı değişken: Sivrisinek sayısı – Bağımsız değişken: Ortam sıcaklığı
4. Bağımlı değişken: Şemsiye talebi – Bağımsız değişken: Aylık yağmurlu gün sayısı

Matematikte bağımlı ve bağımsız değişken

Matematikte neden-sonuç ilişkisi genellikle bir bağımsız değişken ve bir bağımlı değişken kullanılarak modellenir. Böylece bir fonksiyon, bağımlı değişken ile bağımsız değişken arasında var olan matematiksel ilişkiyi tanımlar.

Bağımlı değişkenler genellikle y harfiyle temsil edilirken bağımsız değişkenleri belirtmek için genellikle x harfi kullanılır.

Örneğin y=2x fonksiyonu, bağımsız değişken x bir birim arttığında bağımlı değişken y’nin iki kat arttığını gösterir.

Matematik fonksiyonları hakkında daha fazla bilgi edinmek için iş ortağı web sitemiz function.xyz’yi ziyaret edebilirsiniz.

İstatistikte bağımlı ve bağımsız değişken

Ancak gerçekte iki değişken arasında kesin bir matematiksel fonksiyonla tanımlanabilecek bir ilişki bulmak çok zordur çünkü bazen bağımsız değişkenin aynı değeri bağımlı değişkenin farklı bir değerine neden olur.

Örneğin, bazen daha çok çalışarak daha düşük not alırız ya da tam tersi, daha az çalışarak daha iyi not alırız. Dolayısıyla çalışmaya ayırdığımız saat sayısı, alınan notu etkileyen tek faktör değildir; sınavın zorluğuna veya çalışılan konunun zorluğuna göre de değişebilmektedir.

Bu nedenle istatistikte genellikle biri bağımsız değişken, diğeri bağımlı değişken olacak iki değişken arasında ilişki olup olmadığını belirlemek için birçok deney yapılır. Daha sonra elde edilen sonuçlar, değişkenlerin bağlantılı olup olmadığını kontrol etmek ve eğer öyleyse ne tür bir ilişkiye sahip olduklarını (pozitif, negatif, doğrusal, üstel vb.) görmek için grafiksel olarak temsil edilebilir.

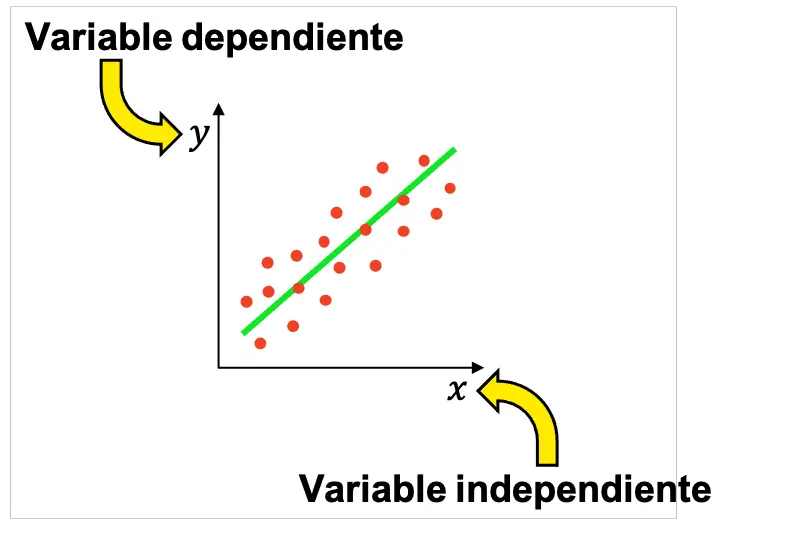
En temel istatistiksel çalışmalar bir bağımsız ve bir bağımlı değişkenle yapılsa da, bir ankette birden fazla bağımsız değişken olabileceğini unutmayın.

İstatistiksel çalışma gerçekleştirildikten sonra, bir tahmin yapmak ve böylece değişkenler arasındaki ilişkiyi modellemek için bir matematiksel fonksiyon hesaplanabilir. Yani normalde önce istatistiksel bir model yapılır, ardından matematiksel bir model yapılır.