Bağımsız değişken

Bu makalede bağımsız değişkenlerin ne olduğu açıklanmaktadır. Böylece bağımsız değişkenin matematik ve istatistikteki anlamını bulacak ve ayrıca bu tür değişkenlerin çeşitli örneklerini göreceksiniz.

Bağımsız değişken nedir?

Bağımsız değişken, değeri başka bir değişkenin değerine bağlı olmayan bir değişkendir. Aksine, bağımsız bir değişkenin değeri değişirse, bağımlı değişkenin değeri de değişir.

Bağımsız bir değişkenin grafiğini çizdiğinizde, genellikle x harfiyle ve x ekseninde (yatay eksen) temsil edilir.

Örneğin, bir mülkü kiraladığınız sürenin uzunluğu, ödeyeceğiniz fiyatı etkileyen bağımsız bir değişkendir. Kiralama süresine karar verilebildiğinden ve değeri fiyata bağlı değişkeni etkilediğinden, tesisler ne kadar uzun süre kullanılırsa o kadar fazla ödemek zorunda kalırlar.

Bağımsız değişkenlere açıklayıcı değişkenler, girdi değişkenleri veya manipüle edilmiş değişkenler de denilebilir.

Bağımsız Değişken Örnekleri

Bağımsız değişkenin tanımını gördükten sonra, kavramı daha iyi anlamak için şimdi bu tür değişkenlerin birkaç örneğine bakalım.

• Ders çalışmak için harcanan zaman (bağımsız değişken) alınan notları (bağımlı değişken) etkilemektedir.
• Bir ürünün fiyatı (bağımsız değişken), ürünü satın almak isteyen kişi sayısını (bağımlı değişken) değiştirir.
• Ortam sıcaklığı (bağımsız değişken) orman yangınlarının sayısını (bağımlı değişken) etkilemektedir.
• Bir ürün için yapılan reklamın (bağımsız değişken), söz konusu ürünün satış adedine (bağımlı değişken) etkisi vardır.
• Bir şehrin sakinlerinin sayısı (bağımsız değişken), şehirdeki taksi sayısına (bağımlı değişken) bağlıdır.

Matematikte bağımsız değişkenler

Matematikte neden-sonuç ilişkisi genellikle bir bağımsız değişken ve bir bağımlı değişken kullanılarak modellenir. Böylece bir fonksiyon, bağımsız değişken ile bağımlı değişken arasında var olan matematiksel ilişkiyi tanımlar.

Bağımsız değişkenler genellikle x harfiyle temsil edilirken, bağımlı değişkenler için y harfi kullanılır.

Örneğin y=2x fonksiyonu, bağımsız değişken x bir birim arttığında bağımlı değişken y’nin iki kat arttığını gösterir.

Matematik fonksiyonları hakkında daha fazla bilgi edinmek için iş ortağı web sitemiz function.xyz’yi ziyaret etmenizi öneririz.

İstatistikte bağımsız değişkenler

Ancak gerçekte iki değişken arasında kesin bir matematiksel fonksiyonla tanımlanabilecek bir ilişki bulmak çok zordur çünkü bazen bağımsız bir değişkenin aynı değeri bağımlı değişkenin farklı bir değerine neden olur.

Örneğin, bazen daha çok çalışarak daha düşük not alırız ya da tam tersi, daha az çalışarak daha iyi not alırız. Dolayısıyla ders çalışarak geçirdiğimiz saat sayısı, alınan notu etkileyen tek faktör değildir; sınavın zorluğuna veya çalışılan konunun zorluğuna göre de değişebilmektedir.

Bu nedenle istatistikte genellikle bağımsız değişken ile bağımlı değişken arasında bir ilişki olup olmadığını belirlemek için birçok deney yapılır. Elde edilen sonuçlar daha sonra değişkenlerin bağlantılı olup olmadığını kontrol etmek ve eğer öyleyse ne tür bir ilişkiye sahip olduklarını (pozitif, negatif, doğrusal, üstel vb.) görmek için grafiksel olarak temsil edilebilir.

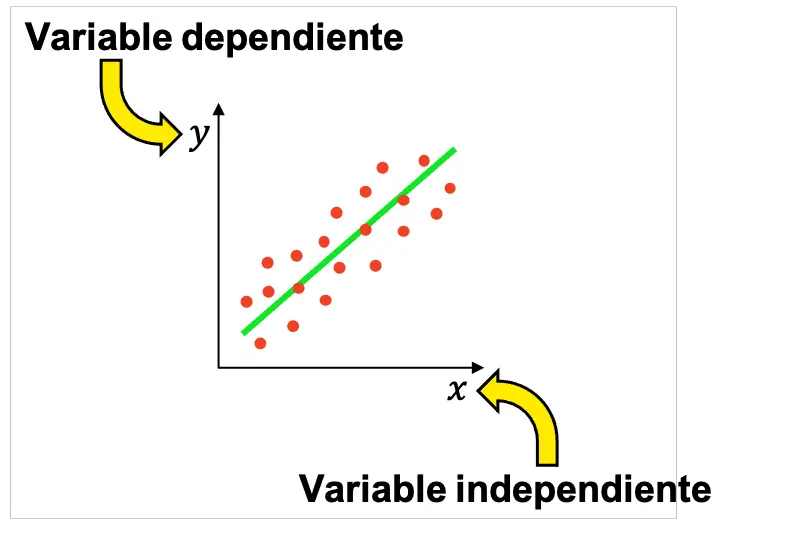
En temel istatistiksel çalışmalar bir bağımsız ve bir bağımlı değişkenle yapılsa da, bir ankette birden fazla bağımsız değişken olabileceğini unutmayın.

İstatistiksel çalışma gerçekleştirildikten sonra, bir tahmin yapmayı ve dolayısıyla değişkenler arasındaki ilişkiyi modellemeyi mümkün kılan bir matematiksel fonksiyon hesaplanabilir. Yani normalde önce istatistiksel bir model, sonra matematiksel bir model yaparsınız.