Poisson dağılımına giriş

Poisson dağılımı istatistikteki en popüler dağılımlardan biridir.

Poisson dağılımını anlamak için öncelikle Poisson deneylerini anlamak faydalı olacaktır.

Balık Deneyleri

Poisson deneyi aşağıdaki özelliklere sahip bir deneydir:

• Deneyin başarılarının sayısı sayılabilir.
• Belirli bir zaman (veya mekan) aralığında meydana gelen ortalama başarı sayısı bilinmektedir.
• Her sonuç bağımsızdır.
• Başarının gerçekleşme olasılığı aralığın boyutuyla orantılıdır.

Poisson deneyinin bir örneği, belirli bir hastanede saat başına doğum sayısıdır. Örneğin, belirli bir hastanenin saatte ortalama 10 doğum yaptığını varsayalım. Bu bir Poisson deneyidir çünkü aşağıdaki dört özelliğe sahiptir:

• Deneyin başarı sayısı sayılabilir – Doğum sayısını sayabiliriz.
• Belirli bir zaman aralığında gerçekleşen ortalama doğum sayısı biliniyor – Saatte ortalama 10 doğum olduğu biliniyor.
• Her sonuç bağımsızdır – Belirli bir saatte bir annenin doğum yapma olasılığı, başka bir annenin doğum yapma olasılığından bağımsızdır.
• Başarının gerçekleşme olasılığı aralığın büyüklüğü ile orantılıdır: zaman aralığı ne kadar uzunsa, doğumun gerçekleşme olasılığı da o kadar yüksek olur.

Bu Poisson deneyine ilişkin olasılıklarla ilgili aşağıdaki gibi soruları yanıtlamak için Poisson dağılımını kullanabiliriz:

• Belirli bir saatte 12’den fazla doğumun meydana gelme olasılığı nedir?
• Belirli bir saatte 5’ten az doğumun meydana gelme olasılığı nedir?
• Belirli bir saatte 8 ila 11 doğumun gerçekleşme olasılığı nedir?

Balık dağıtımı

Poisson dağılımı belirli bir zaman aralığında k başarı elde etme olasılığını açıklar.

Bir Xrastgele değişkeni bir Poisson dağılımını takip ediyorsa, X = k başarısının olasılığı aşağıdaki formülle bulunabilir:

P(X=k) = λ ^k * e ^{– λ} / k!

Altın:

• λ: belirli bir aralıkta meydana gelen ortalama başarı sayısı
• k: başarı sayısı
• e: yaklaşık 2,71828’e eşit bir sabit

Örneğin, belirli bir hastanede saatte ortalama 2 doğum gerçekleştiğini varsayalım. 0, 1, 2, 3 doğum vb. yaşanma olasılığını belirlemek için yukarıdaki formülü kullanabiliriz. belirli bir saatte:

P(X=0) = 2 ⁰ * e ^{– 2/0} ! = 0,1353

P(X=1) = 2 ¹ * e ^{– 2/1} ! = 0,2707

P(X=2) = 2 ² * e ^{– 2/2} ! = 0,2707

P(X=3) = 2 ³ * e ^{– 2/3} ! = 0,1805

Herhangi bir sayıda doğumun olasılığını sonsuza kadar hesaplayabiliriz. Daha sonra bu olasılık dağılımını görselleştirmek için basit bir histogram oluşturuyoruz:

Kümülatif Poisson olasılıklarının hesaplanması

Yukarıdaki formülü kullanarak tek bir Poisson olasılığını (örneğin bir hastanenin belirli bir saatte 3 doğum gerçekleştirme olasılığı) hesaplamak kolaydır, ancak kümülatif Poisson olasılıklarını hesaplamak için bireysel olasılıkları toplamamız gerekir.

Örneğin, hastanenin belirli bir saatte 1 veya daha az doğum yapma olasılığını bilmek istediğimizi varsayalım. Bu olasılığı hesaplamak için aşağıdaki formülü kullanırız:

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

Buna kümülatif olasılık denir çünkü birden fazla olasılığın eklenmesini içerir. Belirli bir saatte k veya daha az doğum yaşanmasının kümülatif olasılığını benzer bir formül kullanarak hesaplayabiliriz:

P(X≤0) = P(X=0) = 0,1353

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

P(X≤2) = P(X=0) + P(X=1) + P(X=2) =0,1353 + 0,2707 + 0,2707 = 0,6767

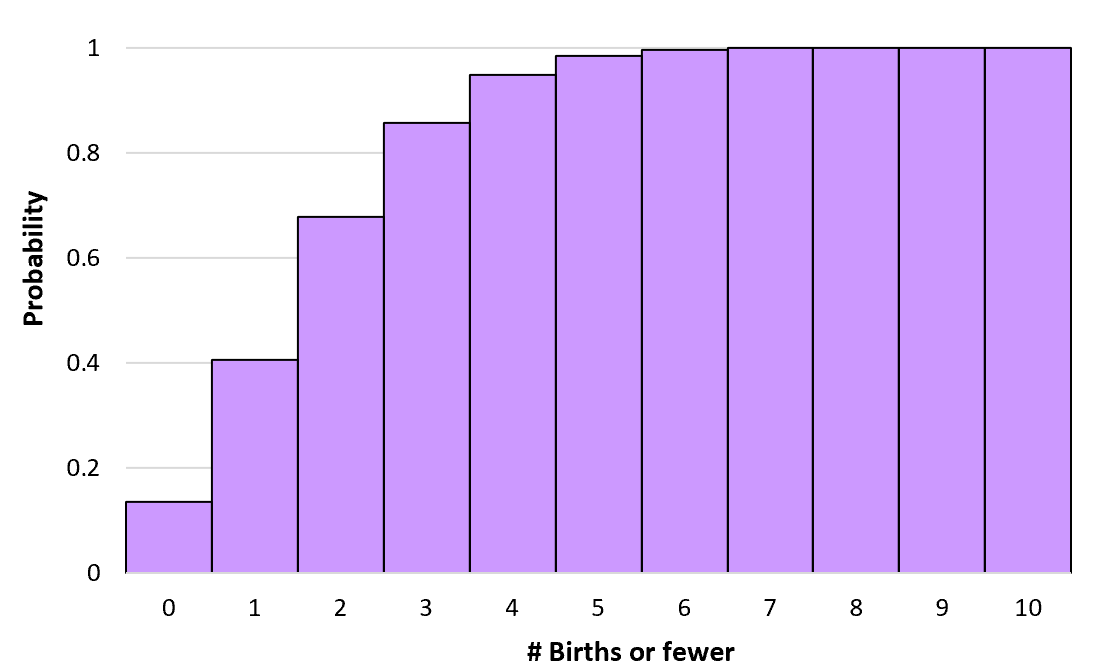
Bu kümülatif olasılıkları herhangi bir doğum sayısı için sonsuza kadar hesaplayabiliriz. Daha sonra bu kümülatif olasılık dağılımını görselleştirmek için bir histogram oluşturabiliriz:

Poisson dağılımının özellikleri

Poisson dağılımı aşağıdaki özelliklere sahiptir:

Dağılımın ortalaması λ’dır .

Dağılımın varyansı da λ’dır .

Dağılımın standart sapması √ λ’dır .

Örneğin bir hastanenin saatte ortalama 2 doğum yaptığını varsayalım.

Belirli bir saatte beklenen ortalama doğum sayısı λ = 2 doğumdur.

Beklediğimiz doğum sayısındaki varyans λ = 2 doğumdur.

Balık dağıtım uygulama problemleri

Poisson dağılımına ilişkin bilginizi sınamak için aşağıdaki alıştırma problemlerini kullanın.

Not: Bu soruların cevaplarını hesaplamak için Poisson dağılımı hesaplayıcısını kullanacağız.

Sorun 1

Soru: Bir web sitesinin saatte 10 satış yaptığını biliyoruz. Belirli bir saatte sitenin tam olarak 8 satış yapma olasılığı nedir?

Cevap: λ = 10 ve x = 8 ile Poisson dağılımı hesaplayıcısını kullanarak P(X=8) = 0,1126’yı buluruz.

Sorun 2

Soru: Bir emlakçının ayda ortalama 5 satış yaptığını biliyoruz. Belirli bir ayda 7’den fazla satış yapma olasılığı nedir?

Cevap: λ = 5 ve x = 7 ile Poisson dağılımı hesaplayıcısını kullanarak P(X>7) = 0,13337’yi buluruz.

Sorun 3

Soru: Belirli bir hastanede saatte 4 doğum gerçekleştiğini biliyoruz. Belirli bir saatte 4 veya daha az doğum olma olasılığı nedir?

Cevap: λ = 4 ve x = 4 ile Poisson dağılımı hesaplayıcısını kullanarak P(X≤4) = 0,62884’ü buluruz.

Ek kaynaklar

Aşağıdaki makaleler Poisson dağılımının farklı istatistiksel yazılımlarda nasıl kullanılacağını açıklamaktadır:

R’de Poisson dağılımı nasıl kullanılır?
Excel’de Poisson dağılımı nasıl kullanılır?
TI-84 Hesap Makinesinde Poisson Olasılıkları Nasıl Hesaplanır?
Poisson dağılımının gerçek dünyadan örnekleri
Balık Dağıtımı Hesaplayıcısı