Poisson dağılımı veya normal dağılım: fark nedir?

Poisson dağılımı ve normal dağılım istatistikte en sık kullanılan olasılık dağılımlarından ikisidir.

Bu eğitimde her dağıtımın hızlı bir açıklamasının yanı sıra dağıtımlar arasındaki iki önemli fark da sunulmaktadır.

Genel bakış: Poisson dağılımı

Poisson dağılımı belirli bir zaman aralığında k başarı elde etme olasılığını açıklar.

Bir Xrastgele değişkeni bir Poisson dağılımını takip ediyorsa, X = k başarısının olasılığı aşağıdaki formülle bulunabilir:

P(X=k) = λ ^k * e ^{– λ} / k!

Altın:

• λ: belirli bir aralıkta meydana gelen ortalama başarı sayısı
• k: başarı sayısı
• e: yaklaşık 2,71828’e eşit bir sabit

Örneğin, belirli bir hastanede saatte ortalama 2 doğum gerçekleştiğini varsayalım. Belirli bir saatte 3 doğum yaşanma olasılığını belirlemek için yukarıdaki formülü kullanabiliriz:

P(X=3) = 2 ³ * e ^{– 2/3} ! = 0,1805

Belirli bir saatte 3 doğum yaşanma olasılığı 0,1805’tir .

Genel bakış: normal dağılım

Normal dağılım, bir rastgele değişkenin belirli bir aralıkta değer alma olasılığını tanımlar.

Normal bir dağılımın olasılık yoğunluk fonksiyonu şu şekilde yazılabilir:

P(X=x) = (1/σ√ 2π )e ^{-1/2((x-μ)/σ) 2}

Altın:

• σ: Dağılımın standart sapması
• μ: Dağılımın ortalaması
• x: rastgele değişkenin değeri

Örneğin, belirli bir su samuru türünün ağırlığının μ = 40 pound ve σ = 5 pound ile normal olarak dağıldığını varsayalım.

Bu popülasyondan rastgele bir su samuru seçersek, ağırlığının 38 ila 42 pound arasında olma olasılığını bulmak için aşağıdaki formülü kullanabiliriz:

P ( ^{38 < /5) 2} = 0,3108

Rastgele seçilen su samuru ağırlığının 38 ile 42 pound arasında olma olasılığı 0,3108’dir .

Fark #1: Gizli vs. Sürekli Veri

Poisson dağılımı ile normal dağılım arasındaki ilk fark, her olasılık dağılımının modellediği veri türüdür.

Yalnızca sıfıra eşit veya sıfırdan büyük tam sayı değerleri alabilen ayrık verilerle çalışırken Poisson dağılımı kullanılır. İşte bazı örnekler:

• Çağrı merkezinde saat başına alınan çağrı sayısı
• Bir restoranda günlük müşteri sayısı
• Aylık trafik kazası sayısı

Her senaryoda rastgele değişken yalnızca 0, 1, 2, 3 vb. değerini alabilir.

Negatif sonsuzdan pozitif sonsuza kadar herhangi bir değer alabilen sürekli verilerle çalışırken normal dağılım kullanılır. İşte bazı örnekler:

• Belirli bir hayvanın ağırlığı
• Belirli bir bitkinin yüksekliği
• Kadınların maraton süreleri
• Santigrat cinsinden sıcaklık

Bu senaryolarda rastgele değişkenler -11,3, 21,343435, 85 vb. gibi herhangi bir değeri alabilir.

Fark #2: dağılımların şekli

Poisson dağılımı ile normal dağılım arasındaki ikinci fark dağılımların şeklindedir.

Normal bir dağılım her zaman çan şekline sahip olacaktır:

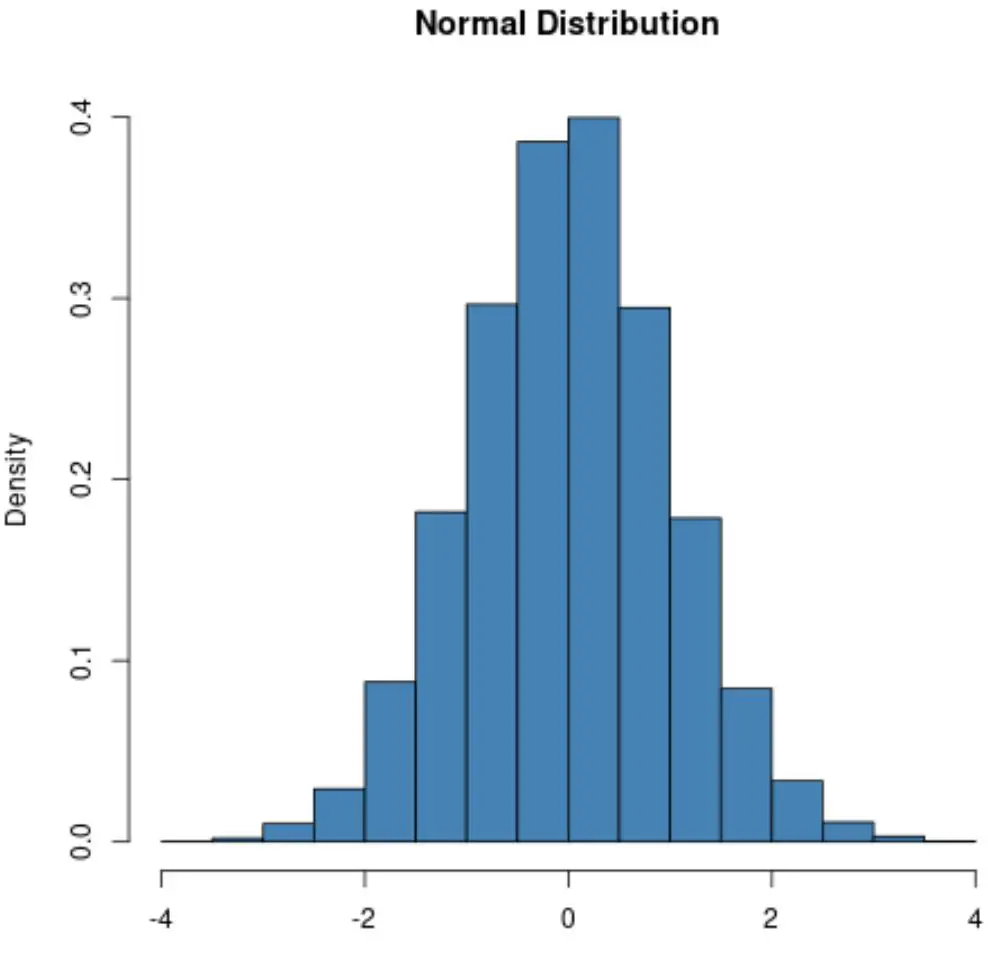
Ancak Poisson dağılımının şekli dağılımın ortalama değerine bağlı olarak değişmektedir.

Örneğin, μ = 3 gibi ortalama değeri küçük olan bir Poisson dağılımı güçlü bir şekilde sağa çarpık olacaktır:

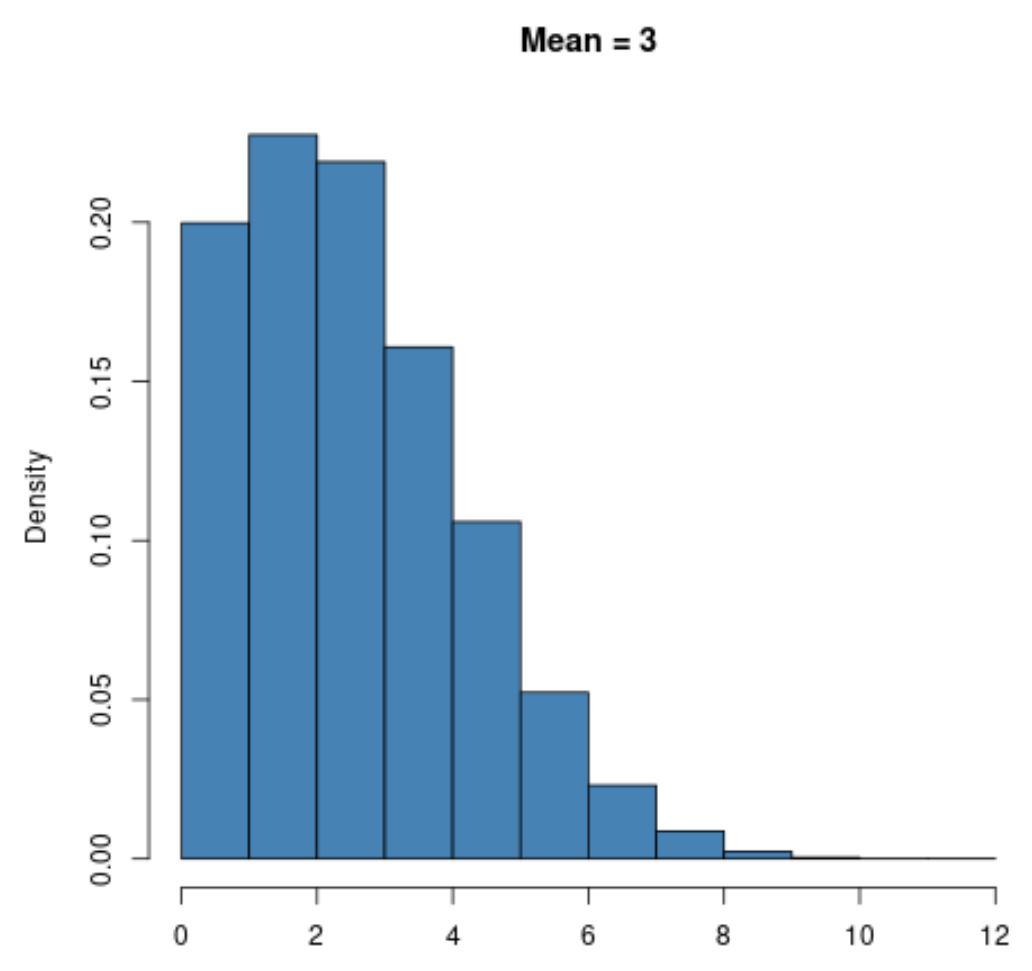
Ancak μ = 20 gibi daha büyük bir ortalama değere sahip bir Poisson dağılımı, tıpkı normal dağılım gibi çan şekli sergileyecektir:

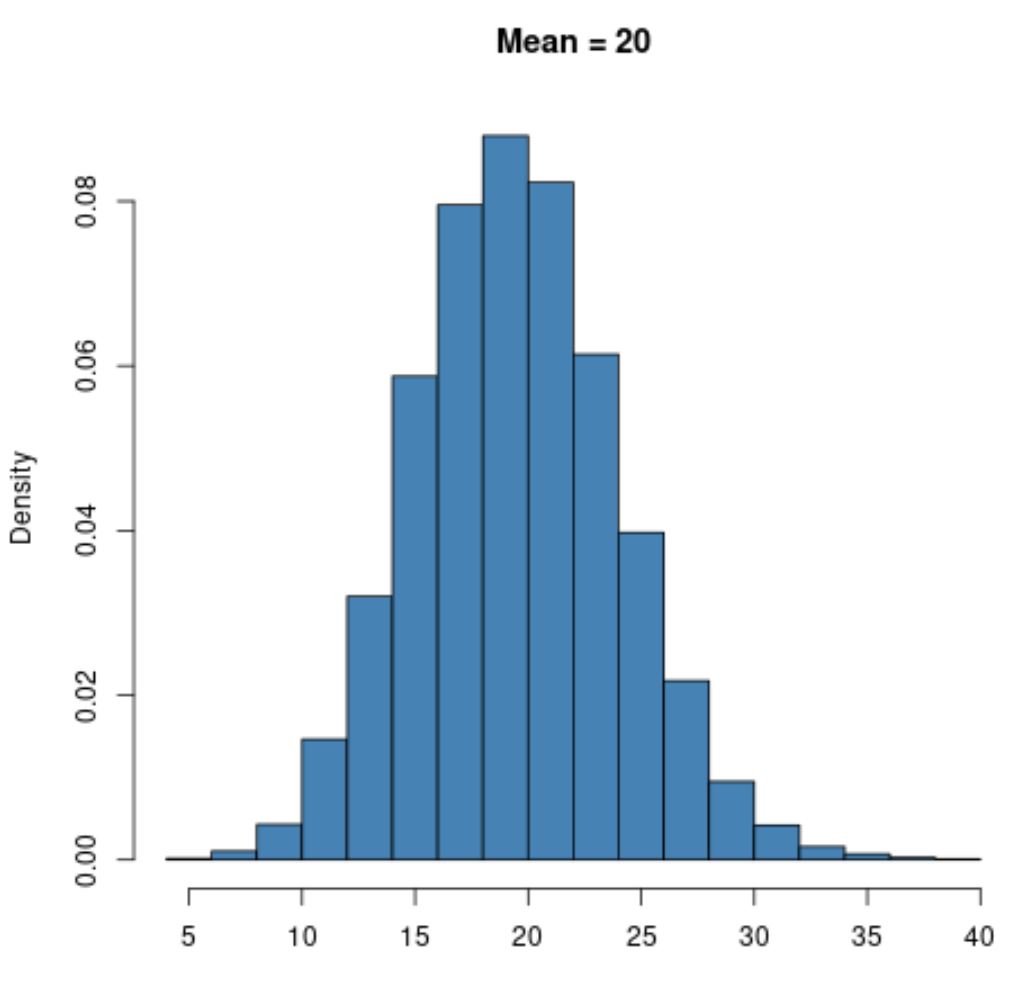
Bir Poisson dağılımının alt sınırının, ortalamanın değerinden bağımsız olarak her zaman sıfır olacağını unutmayın, çünkü bir Poisson dağılımı yalnızca sıfıra eşit veya sıfırdan büyük tam sayı değerleri ile kullanılabilir.

Ek kaynaklar

Aşağıdaki eğitimler Poisson dağılımı hakkında ek bilgi sağlar:

Poisson dağılımına giriş
Poisson dağılımının dört hipotezi
Poisson dağılımının 5 somut örneği

Aşağıdaki eğitimler normal dağılım hakkında ek bilgi sağlar:

Normal dağılıma giriş
Normal dağılımın 6 somut örneği
Normal Dağıtım Veri Kümesi Oluşturucu