Spss'de fisher'in kesin testi nasıl gerçekleştirilir
Fisher’in kesin testi, iki kategorik değişken arasında anlamlı bir ilişki olup olmadığını belirlemek için kullanılır.
Genellikle 2×2’lik bir tabloda bir veya daha fazla hücre sayısı 5’ten az olduğunda ki-kare bağımsızlık testine alternatif olarak kullanılır.
Bu eğitimde Fisher’in kesin testinin SPSS’de nasıl gerçekleştirileceği açıklanmaktadır.
Örnek: Fisher’in SPSS’deki kesin testi
Belirli bir üniversitede cinsiyetin siyasi parti tercihiyle ilişkili olup olmadığını bilmek istediğimizi varsayalım. Bunu araştırmak için kampüsteki 25 öğrenciyle rastgele anket yapıyoruz. Demokrat veya Cumhuriyetçi öğrencilerin cinsiyetlerine göre sayıları aşağıdaki tabloda gösterilmektedir:
| Demokrat | Cumhuriyetçi | |
|---|---|---|
| Dişi | 8 | 4 |
| Erkek | 4 | 9 |
Cinsiyet ile siyasi parti tercihi arasında istatistiksel olarak anlamlı bir ilişki olup olmadığını belirlemek için SPSS’de Fisher’in kesin testini gerçekleştirmek üzere aşağıdaki adımları kullanabiliriz:
Adım 1: Verileri girin.
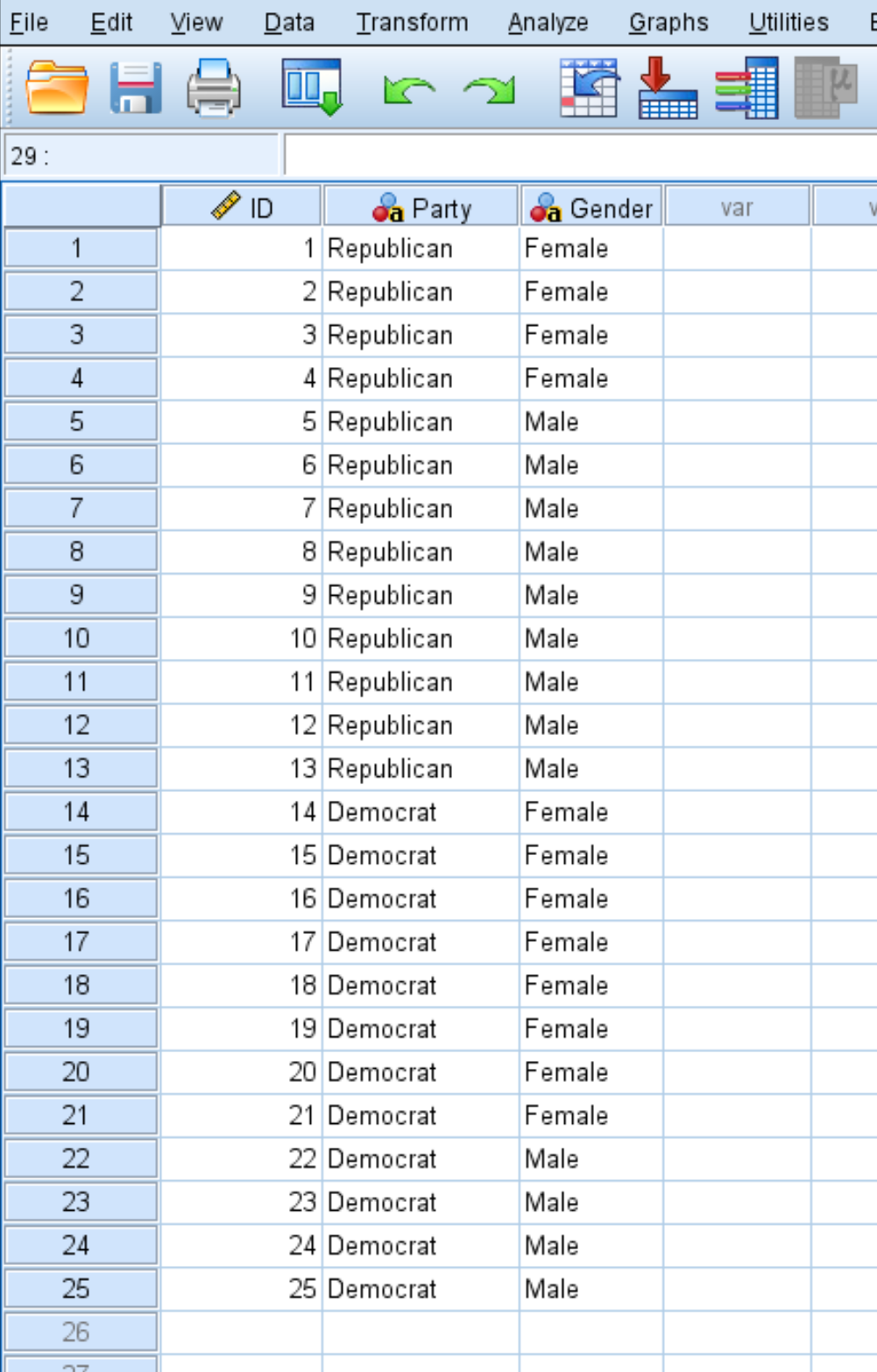
Öncelikle verileri aşağıda gösterildiği gibi girin:
Her satırda bireyin kimliği, siyasi parti tercihi ve cinsiyeti görüntülenir.
Adım 2: Fisher’in kesin testini gerçekleştirin.
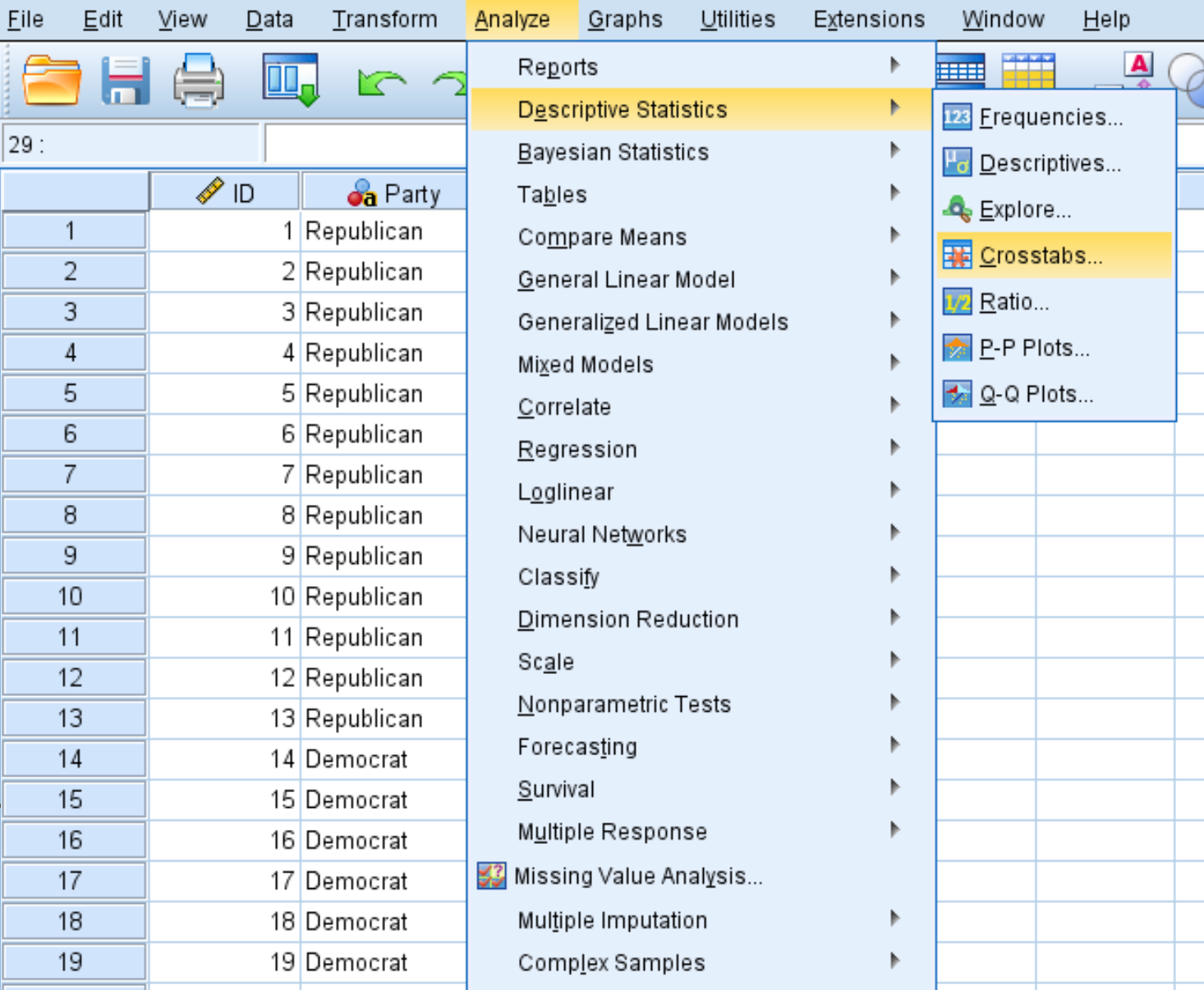
Analiz sekmesini, ardından Tanımlayıcı İstatistikler’i ve ardından Çapraz Tablolar’ı tıklayın:
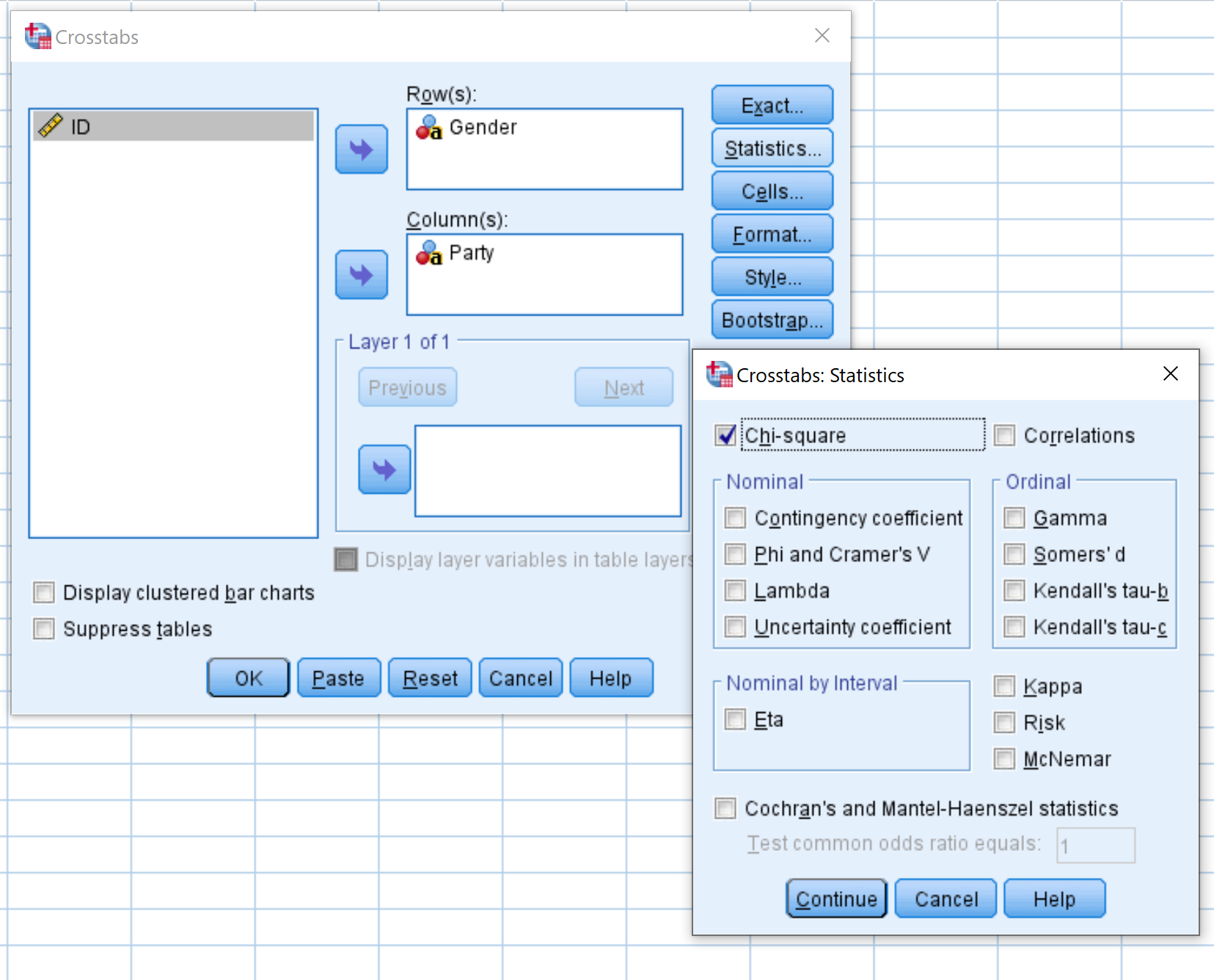
Cinsiyet değişkenini Satırlar etiketli alana ve Parça değişkenini Sütunlar etiketli alana sürükleyin. Daha sonra İstatistikler etiketli düğmeye tıklayın ve Ki Kare’nin yanındaki kutunun işaretli olduğundan emin olun. Daha sonra Devam’ı tıklayın.
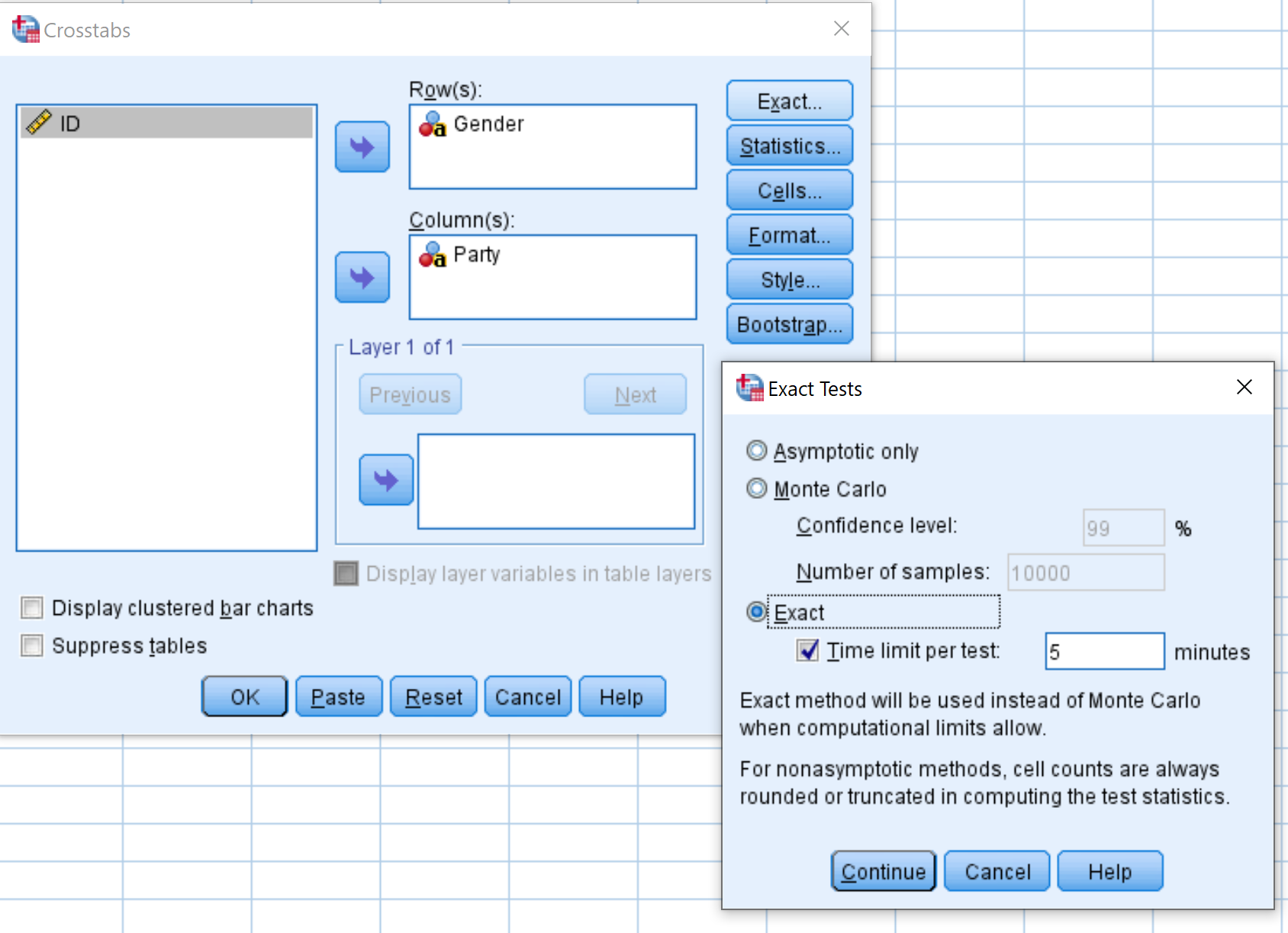
Daha sonra, Tam etiketli düğmeye tıklayın ve Tam’ın yanındaki kutunun işaretli olduğundan emin olun. Daha sonra Devam’ı tıklayın.
Son olarak Fisher’in kesin testini gerçekleştirmek için Tamam’a tıklayın.
Adım 3: Sonuçları yorumlayın.
Tamam’a tıkladığınızda Fisher’in kesin testinin sonuçları görüntülenecektir:
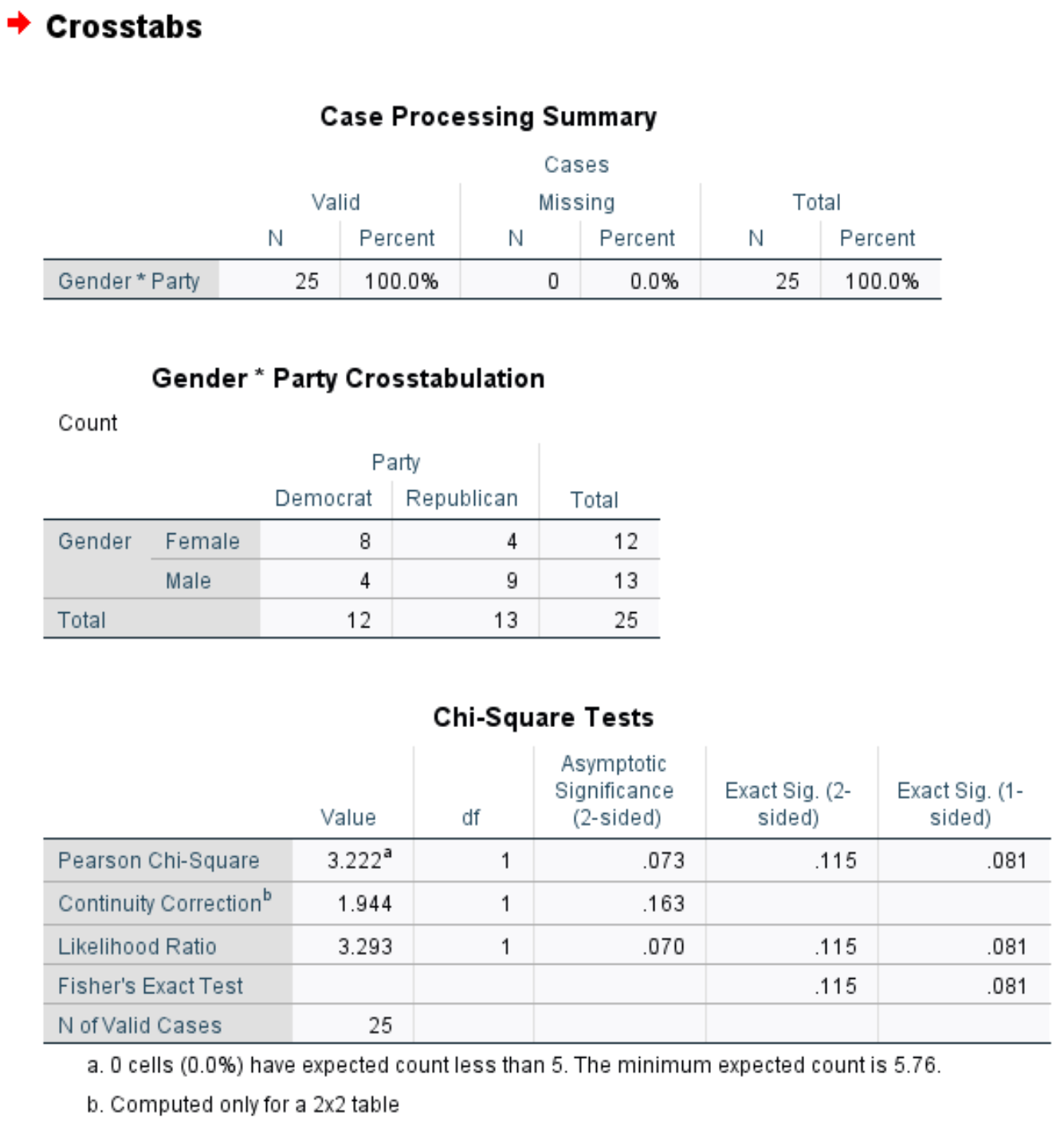
İlk tablo veri kümesindeki eksik vakaların sayısını gösterir. Bu örnekte 0 adet eksik vakanın olduğunu görebiliriz.
İkinci tablo, cinsiyete ve siyasi parti tercihine göre toplam kişi sayısının çapraz tablosunu sunmaktadır.
Üçüncü tablo Fisher’in kesin testinin sonuçlarını göstermektedir. Test için aşağıdaki iki p değerini görebiliriz:
- İki taraflı p değeri: 0,115
- Tek taraflı p değeri: 0,081
Fisher’in kesin testinin sıfır hipotezi, iki değişkenin bağımsız olduğu yönündedir. Bu durumda boş hipotezimiz cinsiyet ve siyasi parti tercihinin bağımsız olduğu yönündedir ve bu iki kuyruklu bir testtir, dolayısıyla 0,115’lik iki kuyruklu p değerini kullanırız.
Bu p değeri 0,05’ten küçük olmadığından sıfır hipotezini reddetmiyoruz. Bu nedenle cinsiyet ile siyasi parti tercihi arasında anlamlı bir ilişki olduğunu söyleyecek yeterli kanıtımız yok.