Excel'de fisher'ın kesin testi nasıl gerçekleştirilir

Fisher’in kesin testi, iki kategorik değişken arasında anlamlı bir ilişki olup olmadığını belirlemek için kullanılır. Genellikle 2×2’lik bir tabloda bir veya daha fazla hücre sayısı 5’ten az olduğunda ki-kare bağımsızlık testine alternatif olarak kullanılır.

Bu eğitimde Fisher’ın kesin testinin Excel’de nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: Fisher’in Excel’deki kesin testi

Belirli bir üniversitede cinsiyetin siyasi parti tercihiyle ilişkili olup olmadığını bilmek istediğimizi varsayalım. Bunu araştırmak için kampüsteki 25 öğrenciyle rastgele anket yapıyoruz. Demokrat veya Cumhuriyetçi öğrencilerin cinsiyetlerine göre sayıları aşağıdaki tabloda gösterilmektedir:

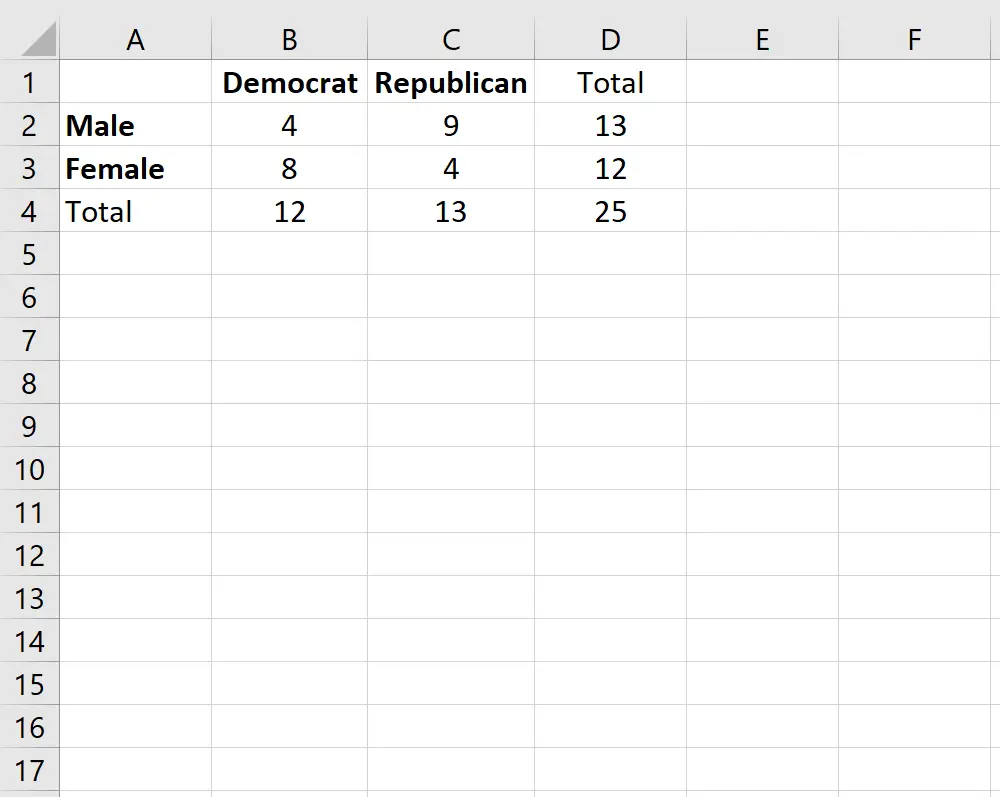
Cinsiyet ile siyasi parti tercihi arasında istatistiksel olarak anlamlı bir ilişki olup olmadığını belirlemek için Fisher’in kesin testini yapabiliriz.

Excel’in bu testi gerçekleştirmek için yerleşik bir işlevi olmasa da, testi gerçekleştirmek için aşağıdaki sözdizimini kullanan hipergeometrik işlevi kullanabiliriz:

=HİPGEOM.DAĞ(örnek_s; örnek_sayı, nüfus_s, pop_sayı, kümülatif)

Altın:

• sample_s = örnekteki “başarılıların” sayısı
• number_sample = örnek boyutu
• nüfus_s = popülasyondaki “başarıların” sayısı
• number_pop = nüfus büyüklüğü
• kümülatif = DOĞRU ise bu, kümülatif dağılım işlevini döndürür; YANLIŞ ise bu, olasılık kütle fonksiyonunu döndürür. Amaçlarımız doğrultusunda her zaman TRUE ifadesini kullanacağız.

Bu fonksiyonu örneğimize uygulamak için 2×2 tablosundaki dört hücreden birini kullanmak üzere seçeceğiz. Herhangi bir hücre işe yarayacaktır, ancak bu örnek için sol üstteki “4” değerine sahip hücreyi kullanacağız.

Daha sonra fonksiyon için aşağıdaki değerleri dolduracağız:

= HİPGEOM.DAĞ (bireysel hücredeki değer, toplam sütun sayısı, toplam satır sayısı, toplam örnek boyutu, DOĞRU)

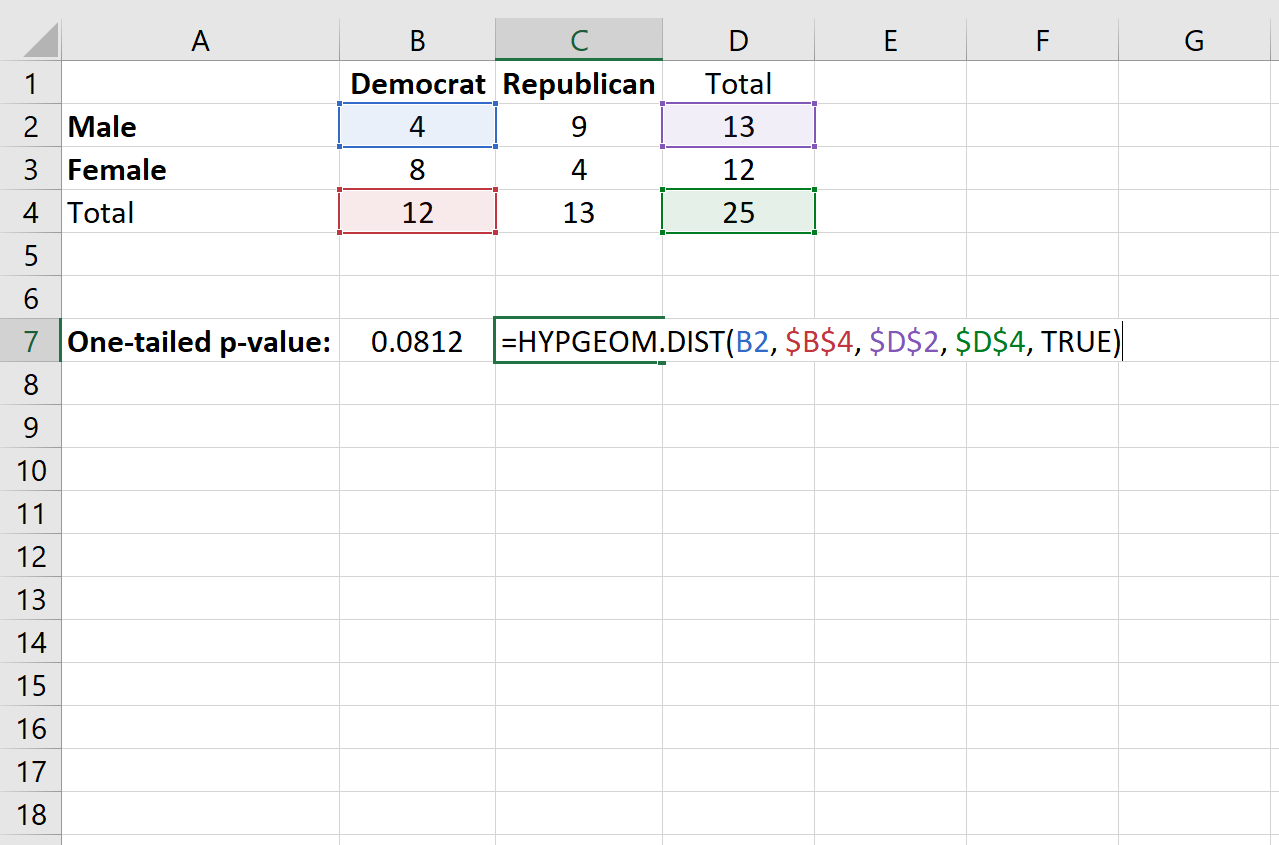
Bu, 0,0812’lik tek taraflı bir p değeri üretir.

Testin iki taraflı p değerini bulmak için aşağıdaki iki olasılığı toplayacağız:

• İlgili hücrede x “başarı” elde etme olasılığı. Bizim durumumuzda bu, 4 başarı elde etme olasılığıdır (bu olasılığı zaten 0,0812 olarak bulmuştuk).
• 1 – ilgilenilen hücrede bulunma olasılığı (toplam sütun sayısı – x “başarı”). Bu durumda Demokrat için toplam sütun sayısı 12’dir, yani 1 – (8 “başarı” olasılığı) bulacağız.

İşte kullanacağımız formül:

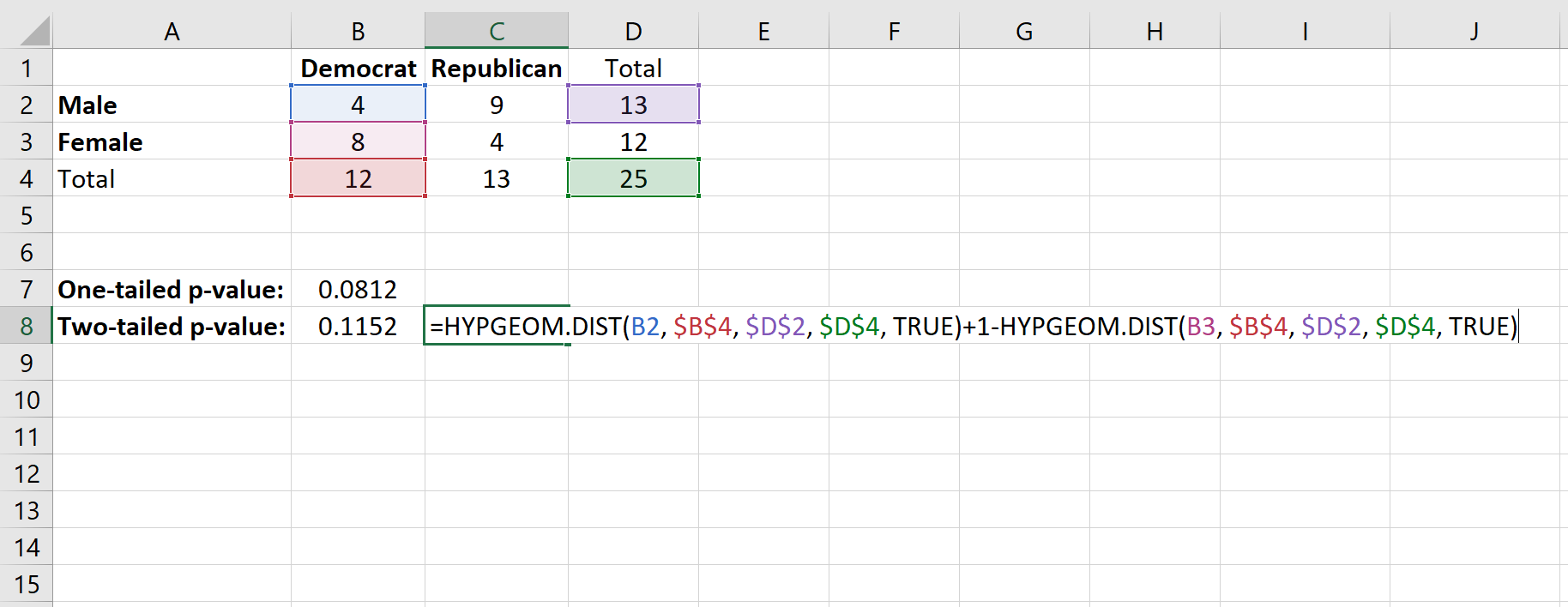
Bu, 0,1152’lik iki kuyruklu bir p değeri üretir.

Her iki durumda da, ister tek kuyruklu ister iki kuyruklu test yapsak, p değeri 0,05’ten az değildir, dolayısıyla sıfır hipotezini reddedemeyiz. Başka bir deyişle cinsiyet ile siyasi parti tercihleri arasında anlamlı bir ilişki olduğunu söyleyecek yeterli kanıtımız yok.

Ek kaynaklar

Excel’de Ki-Kare Bağımsızlık Testi Nasıl Yapılır?
Excel’de Ki Kare Uyum Testi Nasıl Yapılır?
Excel’de Cramer’in V’si Nasıl Hesaplanır?