Basit rastgele örnekleme

İle Dr.benjamin anderson Ağustos 6, 2023 İstatistik 0 Yorum

Bu makalede basit rastgele numunenin ne olduğunu ve ne tür basit rastgele numunelerin bulunduğunu öğreneceksiniz. Ayrıca basit rastgele örneklemenin nasıl yapıldığını bir örnek üzerinden açıklıyoruz. Son olarak basit rastgele örneklemenin avantaj ve dezavantajlarının neler olduğunu görebileceksiniz.

Basit rastgele örnekleme nedir?

İstatistikte basit rastgele örnekleme , bir çalışma için örneklemi seçmek için kullanılan olasılıksal bir yöntemdir. Basit rastgele örneklemenin temel özelliği, istatistiksel popülasyonun her bir elemanına, incelenen numuneye dahil edilme olasılığının aynı olmasıdır.

Basit rastgele örneklemede, örnek öğeler rastgele seçilir, dolayısıyla ortaya çıkan örnek tamamen rastgele olur.

Bu nedenle, basit rastgele örnekleme kullanıldığında, belirli bir numuneyi elde etme olasılığı, herhangi bir başka numuneyi elde etme olasılığına eşittir. Aşağıda bu olasılığın nasıl hesaplandığını göreceğiz.

Bir örnekten bireyleri seçmenin başka yollarının da olduğunu unutmayın. En çok kullanılan örnekleme türleri başlıca şunlardır:

Basit rastgele örnekleme
Tabakalı örnekleme
Sistematik örnekleme
Küme örneklemesi

Basit rastgele örnekleme kavramı kesinlikle anlaşılması en kolay türdür, ancak bazen tam da rastgele doğasından dolayı uygulanması en karmaşık olanı haline gelir.

Basit rastgele örnekleme nasıl yapılır?

Basit rastgele örnekleme gerçekleştirme adımları aşağıdaki gibidir:

Nüfusun tüm unsurlarını içeren bir liste yapın.
Popülasyondaki her öğeye sıralı bir sayı (1, 2, 3,…, n) atayın .
İstediğiniz numune boyutunu ayarlayın.
Seçilen örnek boyutu kadar sayı üretmek için rastgele sayı üreteci kullanın.
Oluşturulan numaralara atanan bireyler, örneklemin parçası olmak üzere seçilen kişilerdir.

Rastgele sayılar üretmek için çeşitli yöntemler vardır; en geleneksel olanları piyango yöntemi ve sayı tablosu yöntemidir:

Piyango yöntemi, tüm sayıları bir kutuya koymayı, karıştırmayı ve ardından rastgele sayıları çekmeyi içerir.
Sayı tablosu yöntemi, tüm olası sayıları içeren bir tablodan sayıların rastgele seçilmesini içerir.

Önceki iki yöntemden birini de kullanabilseniz de, bunlar daha fazla zaman gerektirir ve daha küçük örneklem boyutlarına daha uygundur. Şu anda rastgele sayıları daha hızlı üretmek için bilgisayar programları kullanılıyor, örneğin Excel programını kullanabilirsiniz.

Öte yandan örnekleme hatasının minimum düzeyde olması için örneklem büyüklüğünün yeterli olması gerektiğini de dikkate almalısınız. İdeal örneklem büyüklüğünü bulmak önemsiz değildir; Eğer bu konuda şüpheleriniz varsa bunun nasıl yapılacağını anlattığımız yazımızı sitemizde araştırabilirsiniz.

Basit Rastgele Örnekleme Örneği

Basit rastgele örneklemenin tanımını gördükten sonra, bu tür örneklemenin nasıl yapıldığına dair çözümlenmiş bir örnek göreceğiz.

Örneğin bir şirkette 2000 işçi varsa ve 400 işçiden oluşan bir örneklemle istatistiksel bir çalışma yapmak istiyorsak, basit tesadüfi örneklemeyle örneklemde yer alacak bireyleri seçmek için ilk yapmamız gereken şey; Her çalışana 1’den 2000’e kadar bir sayı atanır.

Numaralar atandıktan sonra rastgele 400 numara seçmemiz gerekiyor. Bu durumda örneklem boyutu oldukça büyük olduğundan Excel gibi bilgisayar yazılımlarını kullanmak en iyisidir.

Daha sonra çalışmaya katılmak üzere seçilen 400 işçi, bir önceki adımda atanan sayısı belirlenen işçiler olacaktır.

Bu örnekte 400 öğenin yeterince temsili bir örneklem büyüklüğü olduğu kabul edildi, ancak mantıksal olarak bu sayı denemeye bağlı olarak değişecektir.

Basit Rastgele Örnekleme Türleri

İki tür basit rastgele örnekleme vardır:

Değiştirmeli basit rastgele örnekleme : örnekleme çerçevesinin seçilen öğesi döndürülür ve tekrar seçilebilir.
Değiştirmeden basit rastgele örnekleme : Örneğin parçası olarak seçilen öğe silinir ve artık seçilemez.

Değiştirmeli basit rastgele örnekleme, numuneden bir öğeyi seçmek için tamamen aynı işlem her zaman tekrarlandığından, en basit örnekleme türüdür. Bununla birlikte, yerine koymadan basit rastgele örnekleme daha kesin olduğu için daha yaygın olarak kullanılmaktadır. Her iki tür de aşağıda daha ayrıntılı olarak açıklanmaktadır.

Değiştirme ile basit rastgele örnekleme

Değiştirmeli basit rastgele örnekleme, seçilen her öğenin örnekleme çerçevesine geri gönderilmesini ve böylece onu tekrar seçme olasılığının ortaya çıkmasını içerir.

Bu nedenle, tek bir öğenin birden çok kez seçilmesiyle bir örnek elde etmek mümkündür, ancak bu çok düşük bir ihtimaldir.

Matematiksel olarak bu çok basit bir örnekleme türüdür çünkü her bir çıkarmanın olasılığı aynıdır. Bu örnekleme tekniğini diğerlerinden önce çalışmaya başlamanın nedeni budur.

Değiştirmeli basit rastgele örneklemede, belirli bir sırayla numune alma olasılığı aşağıdaki formül kullanılarak hesaplanabilir:

$P=\cfrac{1}{N^n}$

Olmak

$N$

popülasyonun toplam element sayısı ve

$n$

Gerçekleştirilecek bağımsız ekstraksiyonların sayısı.

Sıra önemli olmadığında ise numune alma olasılığı aşağıdaki ifade kullanılarak hesaplanır:

$P=\cfrac{n!}{\displaystyle N^n\prod_{i=1}^z k_i!}$

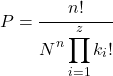
Altın

$n$

bağımsız ekstraksiyonların sayısıdır,

$z$

Örnekteki farklı elementlerin sayısı ve

$k_i$

öğenin kaç kez görünmesini istiyorsunuz?

$i$

örnekte.

Son olarak elemanın dahil olma olasılığını bulmak için

$i$

yani öğenin dahil edilme olasılığı

$i$

Örnekte aşağıdaki formül kullanılmalıdır:

$\displaystyle \pi_i=1-\left(1-\frac{1}{N}\right)^n$

Değiştirilmeden basit rastgele örnekleme

Değiştirmeden basit rastgele örnekleme, bir örnekten istenen örneklem büyüklüğünün gösterdiği kadar çok bireyin seçilmesini içerir, böylece her birey seçildikten sonra tekrar seçilemez. Bu nedenle seçilen her öğe silinir ve değiştirilmez.

Basit tesadüfi örneklemeden bahsettiğimizde, pratikte en çok kullanılan yöntem olduğundan normalde bireylerin değiştirilmediği örneklemeyi kastediyoruz.

Basit rastgele örneklemede değiştirme ile belirli bir sırayla numune alma olasılığını belirlemek için aşağıdaki formül kullanılır:

$P=\cfrac{1}{n!\begin{pmatrix}N\\n\end{pmatrix}}$

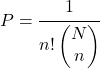
Olmak

$N$

Popülasyondaki toplam element sayısı ve

$n$

Gerçekleştirilecek bağımlı ekstraksiyonların sayısı.

Öte yandan, ekstraksiyon sırasının dikkate alınmaması gerekiyorsa numune alma olasılığı şuna eşittir:

$P=\cfrac{1}{\begin{pmatrix}N\\n\end{pmatrix}}$

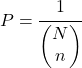
Son olarak, bir öğenin değiştirilmeden basit rastgele örneklemeye dahil edilme olasılığı Laplace kuralı uygulanarak hesaplanır:

$\displaystyle \pi_i=\frac{n}{N}$

Basit Rastgele Örneklemenin Avantajları ve Dezavantajları

Basit rastgele örneklemenin aşağıdaki avantaj ve dezavantajları vardır:

avantaj	Dezavantajları
Anlaması kolay.	Nüfusun tüm unsurlarının bir listesi gereklidir.
Olası tüm numuneler eşit olasılıklıdır.	Büyük örneklem boyutlarında bu çok pahalı olabilir.
Temsili numuneler genellikle elde edilir.	Daha büyük örnekleme hatalarına sahip olma eğilimindedir.
Numune alma işlemini gerçekleştirmek için herhangi bir teknik bilgiye gerek yoktur.	Araştırmacının çalışılan alanda sahip olabileceği bilgiden yararlanılmaz.
Ortalamaları ve sapmaları hızlı bir şekilde hesaplamanıza olanak tanır.	Örnek çok küçükse temsili olmayabilir.
Verileri analiz etmek için istatistiksel yazılım var.	Bireysel görüşme gerektiren çalışmalar için uygun değildir.

Görüldüğü gibi basit rastgele örneklemenin temel özelliklerinden biri anlaşılmasının ve açıklanmasının kolay olmasıdır. Aslında örneklemeyi yapan kişinin analiz alanında uzman olmasına gerek yoktur. Ancak bu hem güçlü hem de zayıf bir noktadır çünkü diğer örnekleme türlerinde analistin bilgisinden daha iyi örnekleme elde etmek için yararlanılabilir.

Benzer şekilde, örnekleme rastgele olduğundan, incelenen örneği oluşturacak şu veya bu unsuru alma olasılıkları, diğer örnekleme türlerinden farklı olarak eşit olasılıklıdır.

Genellikle popülasyonu temsil eden örnekler elde edilmesine rağmen, basit rastgele örneklemede örnekleme hatası diğer örnekleme türlerine göre büyüktür. Ayrıca bireylerin büyüklüğü küçükse örneklem temsili bile olmayabilir.

Basit rastgele örneklemenin çok çekici bir özelliği, istatistiksel hesaplamaların hızlı bir şekilde yapılmasına olanak tanıyan bilgisayar programları kullanılarak gerçekleştirilebilmesidir.

Son olarak, basit rastgele örneklemenin, özellikle geniş bir alana yayılmış popülasyonlarda, diğer örnekleme türlerinden daha pahalı olabileceği, çünkü araştırma için daha fazla kaynak kullanılmasını gerektirebileceği unutulmamalıdır. Örneğin, rastgele örnekleme olduğu için, çalışmayı yürütmek üzere seçilen kişiler coğrafi olarak çok geniş bir alana dağılmış olabilir ve bu nedenle yüz yüze görüşme yapmak çok daha pahalı olabilir.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil