Bayes teoremi

İle Ağustos 1, 2023 Olasılık 0 Yorum

Bu makale Bayes teoreminin ne olduğunu ve olasılık ve istatistikte ne için kullanıldığını açıklamaktadır. Böylece Bayes teoreminin formülünün ne olduğunu, Bayes teoreminin çözümlü örneklerini ve bu teoremin uygulamalarının neler olduğunu keşfedeceksiniz.

Bayes teoremi nedir?

Olasılık teorisinde Bayes teoremi , bir olay hakkında önceden bilgi bilindiğinde o olayın olasılığını hesaplamak için kullanılan bir yasadır.

Daha spesifik olarak Bayes teoremi, A olayının belirli bir B olayının olasılığını, belirli bir A olayının olasılığı ile matematiksel olarak ilişkilendirir.

Örneğin, bir kişinin grip olduğunda baş ağrısı yaşama olasılığını önceden biliyorsanız, bir kişinin baş ağrısı olduğunda grip olma olasılığını belirlemek için Bayes teoremini kullanabilirsiniz.

Bayes teoreminin pek çok uygulaması vardır; örneğin tıpta, ekonomide veya teknolojide başka olaylar tarafından koşullandırılan belirli olayların olasılıklarını hesaplamak için kullanılır. Aşağıda Bayes teoreminin farklı uygulamaları hakkında ayrıntılı bilgi vereceğiz.

Bayes teoremi İngiliz matematikçi Thomas Bayes (1702-1761) tarafından icat edildi, ancak ölümünden sonra 1763’te yayınlandı.

➤ Bakınız: Koşullu olasılık

Bayes teoreminin formülü

Bayes teoremi, olasılıkları sıfır olmayan bir dizi birbirini dışlayan olaylardan (A 1 , A 2 ,…, A i ,…, A n ) ve başka bir B olayından oluşan bir örnek uzay verildiğinde, koşullu durumu matematiksel olarak ilişkilendirebileceğimizi söyler. B olayı verildiğinde A i’nin olasılığı ve A i verildiğinde B’nin koşullu olasılığı.

Bayes kuralı olarak da bilinen Bayes teoreminin formülü şöyledir:

Bayes teoreminin formülü, Bayes kuralı

Altın:

  • P(A_i|B)

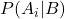
    B olayı verildiğinde A olayının koşullu olasılığıdır ve son olasılık olarak adlandırılır.

  • P(B|A_i)

    A i olayı göz önüne alındığında B olayının koşullu olasılığıdır.

  • P(A_i)

    a priori olasılık olarak adlandırılan, A i olayının meydana gelme olasılığıdır.

Bayes teoremi formülünün paydasının B olayının toplam olasılığı olduğuna dikkat edin.

Bayes teoreminin örneği

Bayes Teoreminin tanımını ve formülünün ne olduğunu gördükten sonra kavramı daha iyi anlamak için Bayes Teoremi ile bir olasılığın nasıl hesaplandığına dair çözümlü bir örnek göreceğiz.

  • Bir elektronik mağazasında X, Y, Z olmak üzere üç marka televizyon satılmaktadır. Satışların %20’sinin arızalı marka televizyonlar olduğu, Y marka televizyonların %3’ünün arızalı, Z marka televizyonların ise %4’ünün arızalı olduğu tahmin edilmektedir. Arızalı bir TV verildiğinde onun Z Marka TV olma olasılığı nedir?

Alıştırma bize bir müşterinin her marka televizyonu satın alma olasılığını veriyor:

  • Olay A 1 : Bir müşteri X marka televizyon satın alıyor → P(A 1 )=0,20
  • Olay A 2 : Bir müşteri Y marka televizyon satın alıyor → P(A 2 )=0,50
  • Olay A 3 : Bir müşteri Z marka televizyon satın alıyor → P(A 3 )=0,30

Ayrıca okuma bize her markanın televizyonunun arızalı olma olasılığını da veriyor:

Olay B: TV arızalı

  • B|A 1 : X marka televizyon verildiğinde televizyon arızalıdır → P(B|A 1 )=0,05
  • B|A 2 : Y marka televizyon verildiğinde televizyon arızalıdır → P(B|A 2 )=0,03
  • B|A 3 : Z marka televizyon verildiğinde televizyon arızalıdır → P(B|A 3 )=0,04

Yani bizi ilgilendiren tüm olayların olasılık ağacı şu şekildedir:

Bayes teoremi ağaç diyagramı

Dolayısıyla, arızalı bir televizyonun Z markası olma olasılığını hesaplamak için Bayes teoremindeki formülü kullanmalıyız:

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

Bu örnekte kullanılan terminolojiyi kullanırsak Bayes’in formülü şuna benzer:

P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}

Buna göre belirli bir arızalı televizyonun Z marka olma ihtimalinin hesaplanması şu şekildedir:

\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,04\cdot 0,30}{0,05\cdot 0,20+0,03\cdot 0,50+0,04\cdot 0,30}\\[2ex]&=0,32\end{aligned}

Sonuç olarak bir televizyonun arızalı olması durumunda Z marka olma ihtimali %32’dir.

Bayes teoreminin uygulamaları

Bayes teoreminin aşağıdakiler dahil birçok uygulaması vardır:

  1. Tıbbi Testler : Bayes teoremi tıpta tanı testlerini geçme olasılığını belirlemek için sıklıkla kullanılır. Örneğin, HIV testi söz konusu olduğunda teorem, test sonucunun pozitif olması durumunda kişinin gerçekten virüse sahip olma olasılığını hesaplamak için kullanılabilir.
  2. Finansal Analiz : Finansta, Bayes teoremi, bir dizi ekonomik değişken göz önüne alındığında, hisse senedi değerindeki artış veya azalış gibi belirli ekonomik olayların meydana gelme olasılığını hesaplamak için kullanılır.
  3. Pazar araştırması : Bayes teoremi, örneğin bir kişinin bu ürünün reklamını gördükten sonra o ürünü satın alma olasılığını belirlemeyi mümkün kılar.
  4. Hava tahmini : Hava durumu modelleri aynı zamanda Bayes teoremini kullanarak gözlemlenen verilere dayanan belirli bir hava tahmininin gerçekleşme olasılığını belirler. Bu, iklim tahminlerinin doğruluğunu artırır.
  5. Bilgisayar Güvenliği – Siber güvenlikte, şüpheli bir etkinliğin gerçekten bilgisayar sistemine yönelik bir saldırı olma olasılığını belirlemek için Bayes teoremi uygulanabilir.

Çözülmüş Bayes Teoremi Problemleri

1. Egzersiz

Nüfusun %1’inin bazı hastalıklardan muzdarip olduğu tahmin edilmektedir. Bu hastalığı tespit etmek için yapılan bir test pozitif vakalarda %95, negatif vakalarda ise %90 doğrudur. Rastgele seçilen bir kişinin testi pozitif çıkarsa, bu kişinin gerçekten hastalığa sahip olma olasılığı nedir?

Alıştırma ifadesi bize aşağıdaki olasılıkları verir:

A 1 : Kişide hastalık var → P(A 1 )=0,01
A 2 : Kişide hastalık bulunmuyor → P(A 2 )=0,99

B: Test pozitif
B|A 1 : Kişide hastalık varsa test pozitiftir → P(B|A 1 )=0,95
B|A 2 : Kişide hastalık olmadığında test pozitiftir → P(B|A 2 )=1-0.90=0.10

Daha sonra, rastgele seçilen bir kişinin testi pozitif çıktığında gerçekten hastalığa sahip olma olasılığını hesaplamak için Bayes kuralı uygulanmalıdır:

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

P(A_1|B)=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}

Böylece değerleri formülde yerine koyuyoruz ve olasılık hesaplamasını gerçekleştiriyoruz:

\begin{aligned}P(A_1|B)&=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}\\[2ex]&=\cfrac{0,95\cdot 0,01}{0,95\cdot 0,01+0,10\cdot 0,99}\\[2ex]&=0,0876\end{aligned}

Kısacası rastgele seçilen bir kişinin testinin pozitif çıkması ve gerçekten hastalığa sahip olma ihtimali %8,76’dır.

Alıştırma 2

Bir hisse senedinin bir gün içerisinde yükselme ihtimali %40, sabit kalma ihtimali %10, düşme ihtimali ise %50 olarak tahmin edilmektedir. Ayrıca, piyasa yükseldiğinde finansal analistin bunu doğru tahmin etme olasılığının %90 olduğunu, piyasa sabit kaldığında tahminin doğru olma olasılığının %75 olduğunu, düşüş durumunda ise tahminin doğru olma olasılığının %75 olduğunu biliyoruz. Doğru tahmin olasılığı %75’tir. %85.%. Bir analist piyasanın düşeceğini öngörüyorsa, gerçekte düşme olasılığı ne kadardır?

Bu durumda, alıştırma ifadesi bize aşağıdaki olasılıkları sağlar:

A 1 : Piyasa bir günde yükselir → P(A 1 )=0,40
A 2 : Piyasa bir gün boyunca sabit kalır → P(A 2 )=0,10
A 3 : Piyasa bir günde yükselir → P(A 3 )=0,50

B: Analist piyasanın düşeceğini öngörüyor
B|A 1 : Analist piyasanın artacağını doğru bir şekilde tahmin ediyor → P(B|A 1 )=0,90
B|A 2 : Analist piyasanın istikrarlı kalacağını doğru bir şekilde tahmin ediyor → P(B|A 2 )=0,75
B|A 3 : Analist piyasanın düşeceğini doğru bir şekilde tahmin ediyor → P(B|A 3 )=0,85

Bir analistin piyasanın düşeceğine dair bir tahminde bulunma ve bunun doğru olma olasılığını belirlemek için Bayes Teoremi formülünü kullanmamız gerekir:

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}

Olasılık değerlerini Bayes formülüne koyarız ve olasılığı hesaplarız:

\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,85\cdot 0,50}{0,90\cdot 0,40+0,75\cdot 0,10+0,85\cdot 0,50}\\[2ex]&=0,4942\end{aligned}

Dolayısıyla bir analistin borsanın düşeceğini söylerken haklı çıkma olasılığı %49,42’dir.

yazar hakkında

Dr.Benjamin Anderson
Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Yorum ekle

E-posta hesabınız yayımlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir