Benford yasası

İle Dr.benjamin anderson Ağustos 3, 2023 Olasılık 0 Yorum

Bu makale Benford yasasının ne olduğunu açıklamaktadır. Ayrıca Benford yasasının nasıl keşfedildiğini ve bu istatistik yasasının uygulamalarının neler olduğunu görebileceksiniz.

Benford Yasası Nedir?

İlk rakam kanunu olarak da adlandırılan Benford yasası , bir veri parçasının ilk rakamının 1 olma olasılığının başka bir sayı olma olasılığından daha büyük olduğunu söyleyen istatistiksel bir yasadır.

Yani Benford kanunu, gerçek hayatta var olan bir sayısal veri kümesinde 1 sayısının, verinin ilk basamağı olarak en çok tekrarlanan sayı olduğunu söylüyor.

Ayrıca sayı ne kadar yüksek olursa birinci olma ihtimali de o kadar düşük olur. Bu nedenle, ilk sayının 1 olma olasılığı 2’den daha yüksektir, ancak 2’nin olasılığı 3’ten daha yüksektir, 3’ün olasılığı 4’ten daha yüksektir vb.

Benford yasası adını Amerikalı Frank Benford’a borçludur. Benford bunu icat etmemiş olmasına rağmen bu istatistiksel kuralı popüler hale getirdi. Aşağıda Benford yasasının kökenini göreceğiz.

Benford Yasası Formülü

Benford Yasası, ilk rakamın belirli bir sayı olma olasılığının, o sayının bir artı bir bölü logaritmasına eşit olduğunu belirtir.

Benford yasasının formülü bu nedenle aşağıdaki gibidir:

$\begin{array}{c}\displaystyle P[X=d]=\log_{10}\left(1+\frac{1}{d}\right)\\[4ex]d=1,2,3,\ldots ,9\end{array}$

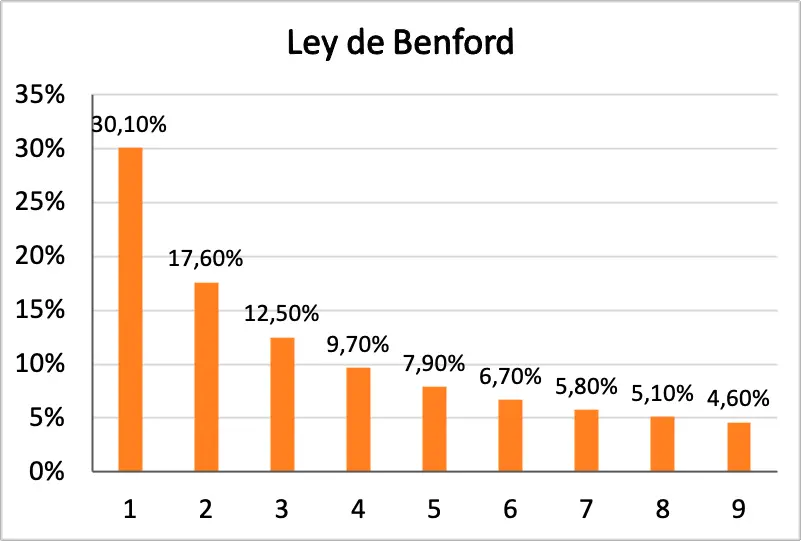
Bu nedenle Benford yasası formülünden her sayının bir veri öğesinin ilk basamağı olma olasılığını çıkarabiliriz. Aşağıdaki tabloda tüm olasılıkların yüzdelerini görebilirsiniz:

Figür	Olasılık ilk numara ol
1	%30,1
2	%17,6
3	%12,5
4	%9,7
5	%7,9
6	%6,7
7	%5,8
8	%5,1
9	%4,6

Ek olarak, aşağıda Benford yasasının tüm olasılıklarının grafiksel olarak temsil edildiği bir histogramı görebilirsiniz:

Benford Yasasının Tarihi

1881’de matematikçi Simon Newcomb, logaritma tablolarının ilk sayfalarının son sayfalarından çok daha fazla kullanıldığını keşfettiğinde Benford yasasını çıkardı. Bu, sayıların ilk rakamlarının eşit olasılıklı olmadığı, ancak 1’in 2’den daha sık olduğu, 2’nin 3’ten daha sık olduğu ve bu şekilde 9’a kadar devam ettiği anlamına geliyordu.

Ancak Newcomb bu kuralın takip edildiğine dair hiçbir istatistiksel kanıt bırakmadı; yalnızca logaritmik tabloların aşınma ve yıpranmasından bir çıkarım yaptı.

Daha sonra, özellikle 1938’de fizikçi Frank Benford aynı gözlemi yaptı ve bunu ampirik olarak doğrulamak için bir deney yaptı. 20 farklı örnekten alınan 20.229 değerden oluşan istatistiksel veri seti üzerinde, her verinin ilk rakamı üzerinde bir çalışma gerçekleştirdi. Böylece sonuçlara dayanarak Benford yasasının gerçekleştiğini gösterdi ve ilk rakamın belirli bir sayı olma olasılığını hesaplamasına olanak tanıyan formülü çıkardı (bu formülü yukarıda gördük).

Kısacası Benford Yasası ilk kez Simon Newcomb tarafından keşfedilmiş olsa da bu istatistik yasasını doğrulayan kişi olduğu için kendisine Frank Benford’un adı verilmiştir.

Benford Yasasının Uygulamaları

Benford yasası, çok farklı alanlarda uygulama alanı bulan istatistiksel bir yasadır. Örneğin Benford yasası ekonomide, biyolojide ve hatta politikada yaygın olarak kullanılmaktadır.

Ekonomide, Benford yasası genellikle veri manipülasyonunu tespit etmek için kullanılır, çünkü bir veri seti Benford yasasına uymuyorsa, bu verinin manipüle edildiğini gösterir. Bu yasa, örneğin olası vergi kaçakçılığı vakalarını tespit etmek için kullanılıyor.

Sonuçlar eşit olasılıklı olduğundan Benford yasasının rastgele olayların doğruluğunu göstermek için kullanılmadığına dikkat edilmelidir. Bu nedenle Benford kuralı piyango sonuçlarını doğrulamak için kullanılamaz.

Öte yandan genetikte Benford yasası, farklı organizma türleri arasındaki genom uzunluğundaki farklılıkları analiz etmek için kullanılabilir.

Son olarak, Benford yasasını uygulayarak seçmen sahtekarlığını tespit etmek için de girişimlerde bulunuldu, ancak bu davadaki yararlılığı sorgulandı.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil