Benjamini-hochberg prosedürüne yönelik bir rehber

İstatistiksel bir test yaptığınızda, sıfır hipoteziniz doğru olsa bile tamamen şans eseri 0,05’ten daha düşük bir p değeri elde etmeniz mümkündür.

Örneğin, belirli bir bitkinin ortalama yüksekliğinin 10 inçten fazla olup olmadığını bilmek istediğinizi varsayalım. Test için boş ve alternatif hipotezleriniz şöyle olacaktır:

H ₀ : μ = 10 inç

H _A : μ > 10 inç

Bu hipotezi test etmek için dışarı çıkıp ölçmek üzere 20 bitkiden oluşan rastgele bir örnek toplayabilirsiniz. Bu bitki türünün gerçek ortalama boyu 10 inç olmasına rağmen, alışılmadık derecede uzun 20 bitkiden oluşan bir örnek seçmiş olmanız mümkündür, bu da sıfır hipotezini reddetmenize yol açar.

Sıfır hipotezi doğru olsa bile (bu bitkinin ortalama yüksekliği aslında 10 inçti), onu reddettiniz. İstatistiklerde buna “yanlış keşif” diyoruz. Bir keşif yaptığınızı, “önemli bir sonuç” elde ettiğinizi iddia ediyorsunuz ama bu aslında yanlış.

Şimdi aynı anda 100 istatistiksel test çalıştırdığınızı hayal edin. 0,05 alfa düzeyi kullanıldığında, tek bir testte yanlış keşif yapma şansı yalnızca %5’tir, ancak çok sayıda test yaptığınız için 100 testten yalnızca 5’inin yanlış keşiflere yol açmasını beklersiniz.

Modern dünyada, teknoloji araştırmacıların aynı anda yüzlerce hatta binlerce istatistiksel test yapmasına olanak tanıdığından, yanlış keşifler yaygın bir sorun olabilir.

Örneğin tıp araştırmacıları aynı anda onbinlerce gen üzerinde istatistiksel testler gerçekleştirebilmektedir. Yalnızca %5’lik bir yanlış keşif oranı bile, yüzlerce testin yanlış keşiflerle sonuçlanabileceği anlamına geliyor.

Yanlış keşif oranını kontrol etmenin bir yolu Benjamini-Hochberg prosedürü adı verilen yöntemi kullanmaktır.

Benjamini-Hochberg prosedürü

Benjamini-Hochberg prosedürü şu şekilde çalışır:

Adım 1: Tüm istatistiksel testlerinizi gerçekleştirin ve her test için p değerini bulun.

Adım 2: Her birine bir sıra atayarak p değerlerini azalan sırada sıralayın: en küçük değerin sırası 1’dir, sonraki en küçük değerin sırası 2’dir, vb.

Adım 3: (i/m)*Q formülünü kullanarak her p değeri için kritik Benjamini-Hochberg değerini hesaplayın

Altın:

i = p değerinin sırası

m = toplam test sayısı

Q = seçtiğiniz yanlış keşif oranı

Adım 4: Kritik değerden küçük en büyük p değerini bulun. Bu p değerinden küçük olan her p değerini anlamlı olarak belirleyin.

Aşağıdaki örnek, bu prosedürün somut değerlerle nasıl gerçekleştirileceğini göstermektedir.

Örnek

Diyelim ki araştırmacılar 20 farklı değişkenin kalp hastalığıyla ilişkili olup olmadığını belirlemek istiyor. Aynı anda 20 ayrı istatistiksel test gerçekleştiriyorlar ve her test için bir p değeri alıyorlar. Aşağıdaki tabloda her test için azalan sırada listelenen p değerleri gösterilmektedir.

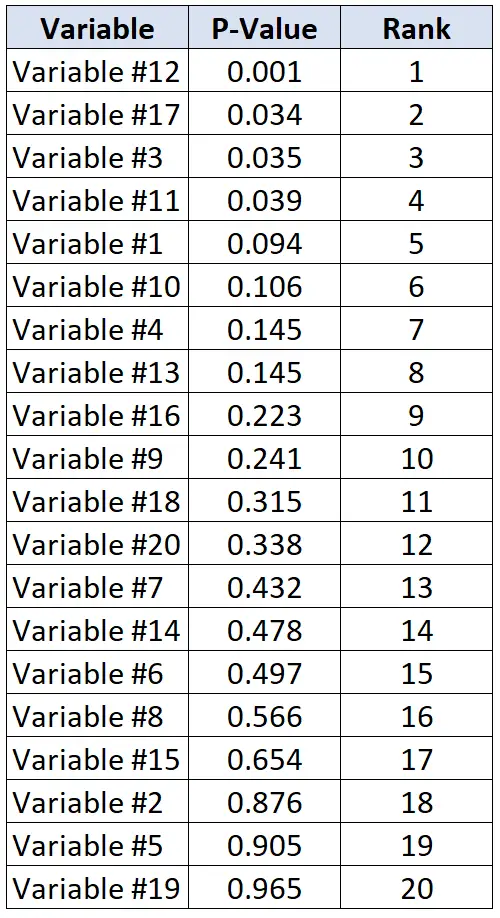
Araştırmacıların %20’lik yanlış keşif oranını kabul etmeye istekli olduklarını varsayalım. Dolayısıyla, her p değeri için kritik Benjamini-Hochberg değerini hesaplamak amacıyla aşağıdaki formülü kullanabiliriz: (i/20)*0,2 burada i = p değerinin sırası.

Aşağıdaki tablo her bir p değeri için kritik Benjamini-Hochberg değerini göstermektedir:

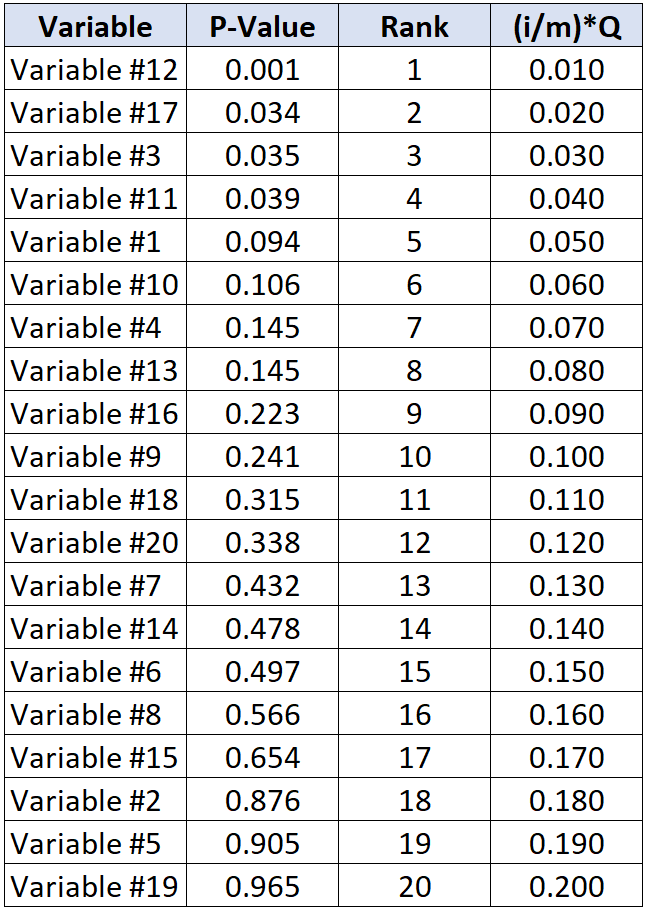
Benjamini-Hochberg kritik değerinin altında en büyük p değerine sahip test #11 değişkenidir; p değeri 0,039 ve BH kritik değeri 0,040’tır.

Dolayısıyla bu test ve p değeri daha küçük olan tüm testler anlamlı kabul edilecektir.

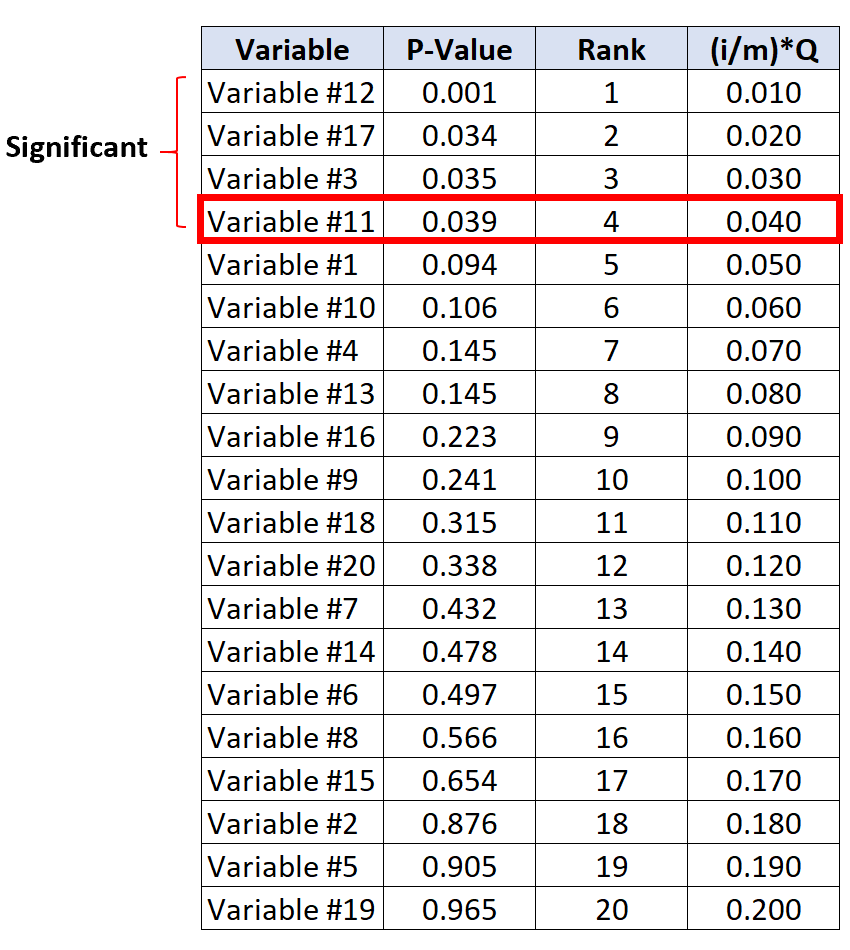
Değişken #17 ve #3’ün BH kritik değerlerinden daha küçük p değerleri olmamasına rağmen, #11 değişkeninden daha küçük p değerlerine sahip olmaları nedeniyle yine de anlamlı kabul edildiklerine dikkat edin.

Yanlış keşif oranı nasıl seçilir

Benjamini-Hochberg prosedüründeki en önemli adımlardan biri yanlış keşif oranının seçilmesidir. Veri toplamadan veya istatistiksel testler yapmadan önce yanlış keşif oranınızı seçmelisiniz.

Tipik olarak, analizinizin keşif aşaması sırasında çok sayıda istatistiksel test gerçekleştireceksiniz ve daha sonra sonuçlarınızı daha fazla araştırmak için bunları diğer testlerle takip edeceksiniz.

Takip testi ucuzsa, daha yüksek bir yanlış keşif oranı ayarlamayı düşünebilirsiniz; çünkü birkaç yanlış keşif yapsanız bile, sonraki testlerde muhtemelen bu yanlış keşifleri keşfedeceksiniz.

Ayrıca önemli bir keşfi kaçırmanın maliyeti yüksekse, önemli hiçbir şeyi kaçırmamak için yanlış keşif oranınızı artırmak isteyebilirsiniz.

Araştırmanızın maliyetine ve önemli bulguları kaçırmamanın önemine bağlı olarak yanlış keşif oranı durumdan duruma değişecektir.

Ek kaynaklar

P değerlerinin ve istatistiksel anlamlılığın açıklaması
Aile başına hata oranı nedir?