Bernoulli dağılımı ve binom dağılımı: fark nedir?

Bir rastgele değişken yalnızca iki olası sonucu varsa Bernoulli dağılımını takip eder: 0 veya 1.

Örneğin, bir kez yazı tura attığımızı varsayalım. p olsun. Bu, yazı gelme olasılığının 1- p olduğu anlamına gelir.

Yani şunu yazabiliriz:

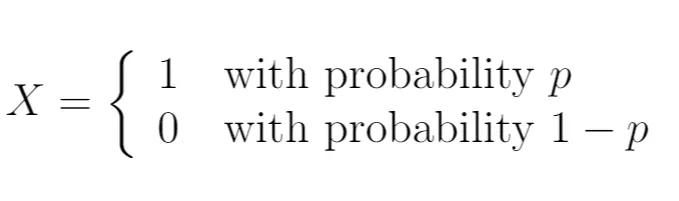
Bu durumda X rastgele değişkeni Bernoulli dağılımını takip eder. Yalnızca iki olası değer alabilir.

Şimdi, eğer bir parayı birden çok kez atarsak, Bernoulli rastgele değişkenlerinin toplamı binom dağılımını izleyecektir.

Örneğin, bir parayı 5 kez attığımızı ve k kez tura gelme olasılığını bilmek istediğimizi varsayalım. Rastgele değişkene benziyor

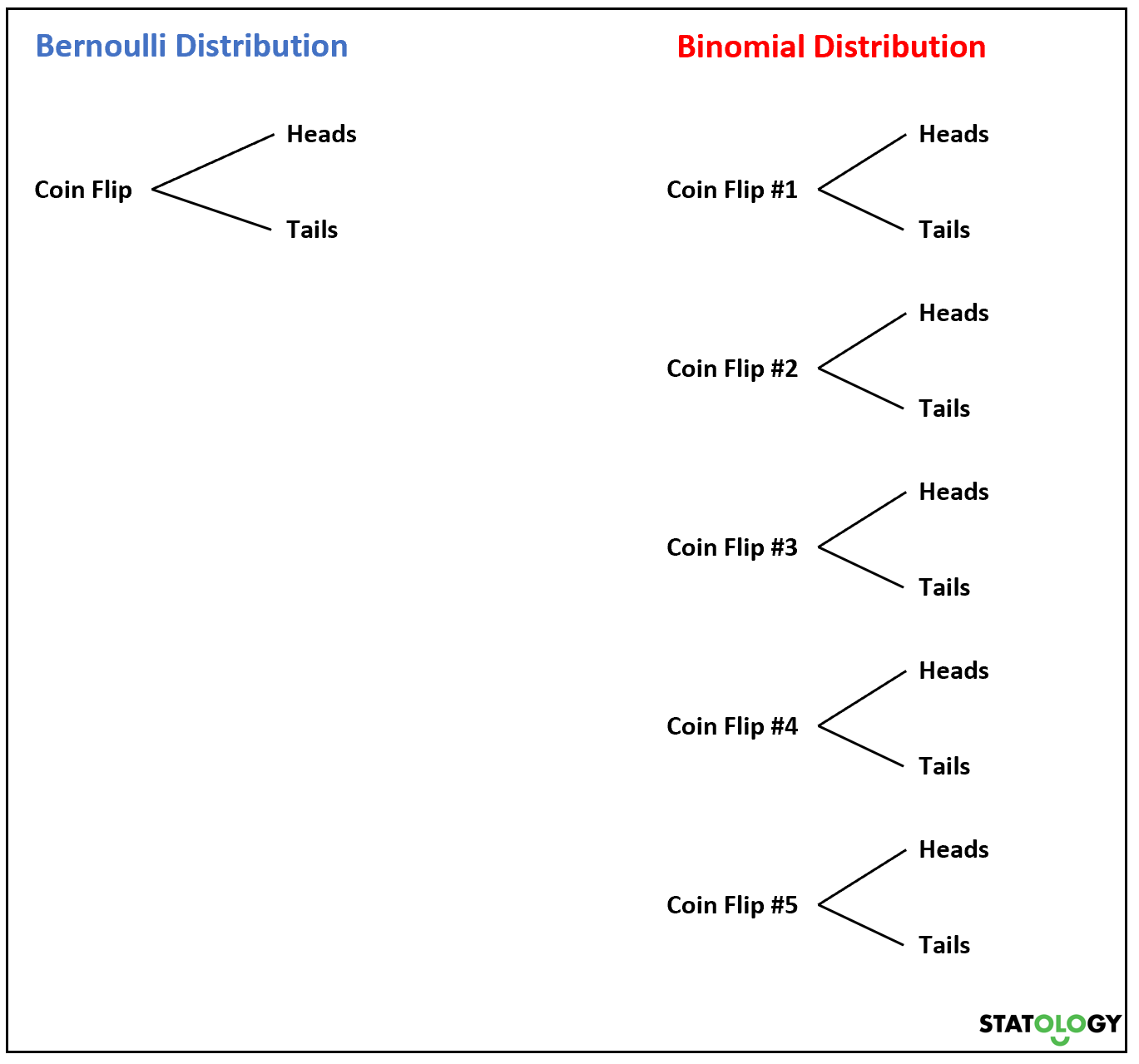
Eğer bir X rastgele değişkeni binom dağılımını takip ediyorsa, X = k başarısının olasılığı aşağıdaki formülle bulunabilir:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Altın:

• n: deneme sayısı
• k: başarı sayısı
• p: belirli bir denemede başarı olasılığı
• _n C _k : n denemede k başarı elde etmenin yollarının sayısı

Örnek: Bir parayı 3 kez attığımızı varsayalım. Bu 3 atışta 0 tura gelme olasılığını belirlemek için yukarıdaki formülü kullanabiliriz:

P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125

n = 1 deneme olduğunda binom dağılımı Bernoulli dağılımına eşdeğerdir.

Önemli notlar

Bernoulli ve Binom dağılımına ilişkin bazı önemli notlar:

1. Bernoulli dağılımını izleyen bir rastgele değişken yalnızca iki olası değer alabilir, ancak binom dağılımını izleyen bir rastgele değişken birkaç değer alabilir.

Örneğin, tek bir yazı tura atışında ya 0 ya da 1 tura gelir. Ancak 5’lik bir seride 0, 1, 2, 3, 4 veya 5 tura gelebiliriz.

2. Bir rastgele değişkenin binom dağılımını takip edebilmesi için, her Bernoulli denemesindeki “başarı” olasılığının eşit ve bağımsız olması gerekir.

Örneğin, “başarıyı” tura gelme olarak tanımlarsak, her atışta başarı olasılığı 0,5 olur ve her atış bağımsızdır; bir atışın sonucu diğerinin sonucunu etkilemez.

Ek kaynaklar

Binom Deneylerine Giriş
Binom dağılımına giriş
Binom dağılımının şeklini anlama