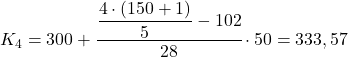Beşte birlik dilimler (istatistikler)

İle Dr.benjamin anderson Ağustos 5, 2023 İstatistik 0 Yorum

Bu yazıda beşte birlik dilimlerin ne olduğunu ve nasıl hesaplandıklarını açıklıyoruz. Beşte birlik dilimlerin hesaplanmasına ilişkin birkaç çözülmüş örnek bulacaksınız ve ayrıca çevrimiçi bir hesap makinesiyle herhangi bir istatistiksel örneğin beşte birlik dilimlerini hesaplayabileceksiniz.

Beşte birlikler nedir?

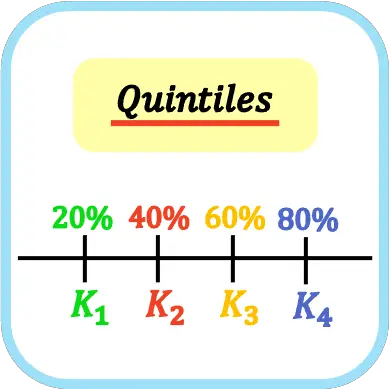
İstatistikte beşte birlik dilimler, bir veri kümesini beş eşit parçaya bölen dört değerdir. Dolayısıyla birinci, ikinci, üçüncü ve dördüncü beşte birlik dilimler örnek verilerin sırasıyla %20, %40, %60 ve %80’ini temsil eder.

Yani, örneğin üçüncü beşte birlik dilimin değeri, toplanan tüm verilerin %60’ından daha yüksek, ancak verilerin geri kalanından daha düşüktür.

Beşte birlik dilimlerin sembolü beşte birlik indeksi olan büyük K harfidir, yani ilk beşte birlik dilim K ₁ , ikinci beşte birlik dilim K ₂ , üçüncü beşte birlik dilim K ₃ ve dördüncü beşte birlik dilim K _4’tür . Her ne kadar Q harfiyle de temsil edilebilse de (kartillerle karışıklık yarattığı için önerilmez).

👉Herhangi bir veri seti için beşlik dilimleri hesaplamak için aşağıdaki hesap makinesini kullanabilirsiniz.

Beşlik dilimler, çeyreklikler, ondalık dilimler ve yüzdelik dilimlerle birlikte merkezi olmayan konumun bir ölçüsüdür. Daha fazla ilgileniyorsanız, bu nicelik türlerinin her birinin ne anlama geldiğini web sitemizden kontrol edebilirsiniz.

Quintile’nin başka bir tanımı olabileceği unutulmamalıdır. Ekonomide beşte birlik dilimler, bir nüfusun gelire göre sıralanan yüzdesini temsil eder veya başka bir deyişle, bir nüfusu gelir düzeylerine göre sıralar. Örneğin, ilk beşte birlik dilim bir nüfustaki insanların en yoksul %20’sine karşılık gelir, ikinci beşte birlik dilim ise nüfusun en düşük gelire sahip %40’ına karşılık gelir, vb.

Beşte birlik dilimler nasıl hesaplanır

Bir numunenin veya istatistiksel popülasyonun beşte birlik dilimlerinin konumunu hesaplamak için, beşte birlik dilim sayısını toplam veri sayısının toplamının bir artısıyla çarpmanız ve sonucu beşe bölmeniz gerekir.

Bu nedenle, beşte birlik dilimlerin formülü şöyledir:

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

Lütfen unutmayın: Bu formülün sonucu bize beşte birlik dilimin değerini değil konumunu söyler. Bu nedenle beşte birlik kısım, formül tarafından elde edilen konumda bulunan veriler olacaktır.

Ancak bazen bu formülün sonucu bize ondalık sayı verir, bu nedenle sonucun ondalık sayı olup olmadığına bağlı olarak iki durumu ayırmamız gerekir:

Formülün sonucu ondalık kısmı olmayan bir sayı ise, beşte birlik kısım yukarıdaki formülün sağladığı konumda bulunan verilerdir.
Formül sonucu ondalık kısmı olan bir sayıysa , beşte birlik değer aşağıdaki ifade kullanılarak hesaplanır:

$K=x_i+d\cdot (x_{i+1}-x_i)$

Burada x _i ve x _i+1, birinci formülle elde edilen sayının aralarında bulunduğu konumların sayılarıdır ve d , birinci formülle elde edilen sayının ondalık kısmıdır.

Bir veri setinin beşte birlik dilimlerini belirlemek için bu kadar çok adım gördüğünüzde korktuysanız endişelenmeyin, aslında oldukça basit. Aşağıdaki iki örneği okuyun, mutlaka çok daha iyi anlayacaksınız.

Not : İstatistik topluluğu beşte birlik dilimlerin nasıl hesaplandığı konusunda hala tam olarak bir fikir birliğine varmamıştır; bu nedenle bunu biraz farklı açıklayan bir kitap bulabilirsiniz.

Beşte birlik dilimleri hesaplama örnekleri

Aşağıda size bir veri serisinden beşte birlik dilimlerin nasıl elde edileceğine dair adım adım çözülmüş iki alıştırma bırakıyoruz. Yani iki olası durumu görebilirsiniz; ilk alıştırmada sonuçlar ondalık değildir, ikinci alıştırmada ise öyledir.

örnek 1

Aşağıdaki veri serilerinin beşte birlik dilimlerini hesaplayın:

Yukarıdaki açıklamada gördüğünüz gibi beşte birlik dilimlerin konumunu bulma formülü şöyledir:

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

n parametresi, 49 olan toplam veri sayısını ifade eder, dolayısıyla ilk beşte birlik kısmın konumunu bulmak için n’yi 49 ile ve k’yi 1 ile değiştirmemiz gerekir:

$\cfrac{1\cdot (49+1)}{5}=10 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_1=205$

Formülden 10 sayısını elde ettik; bu, beşte birlik dilimin sıralı listenin onuncu konumunda olduğu anlamına gelir ve bu da 205 verisine karşılık gelir.

İkinci beşte birlik kısmı hesaplamak için aynı formülü kullanmalısınız ancak k’yi 2 ile değiştirmelisiniz:

$\cfrac{2\cdot (49+1)}{5}=20 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_2=236$

Bu nedenle ikinci beşte birlik sıralı listenin 20 numaralı pozisyonundadır, yani 236 değerindedir.

Yine, beşte birlik dilim 3’ü belirlemek için işlemi tekrarlıyoruz, ancak mantıksal olarak şimdi k’yi 3 ile değiştiriyoruz:

$\cfrac{3\cdot (49+1)}{5}=30 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_3=266$

Dolayısıyla üçüncü beşte birlik dilim, 266’ya karşılık gelen 30. konumda yer alan verilerdir.

Son olarak dördüncü beşte birlik kısmı hesaplamak için formülü tekrar uyguluyoruz:

$\cfrac{4\cdot (49+1)}{5}=40 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_4=286$

Dördüncü beşte birlik dilim bu nedenle 40 konumundadır, yani dördüncü beşte birlik dilim 286’dır.

Örnek 2

Aşağıdaki tabloda toplanan istatistiksel verilerin dörtte birlik dilimini hesaplayın:.

Önceki örnekte olduğu gibi, beşte birlik dilimlerin konumlarını elde etmek için aşağıdaki formülü kullanmanız gerekir:

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

Bu durumda örneklem büyüklüğü 42 gözlemdir, dolayısıyla ilk beşte birlik dilimin konumunu bulmak için n parametresini 42 ve k parametresini 1 ile değiştirmemiz gerekir:

$\cfrac{1\cdot (42+1)}{5}=8,6$

Ancak ilk örnekten farklı olarak bu sefer formül bize ondalık bir sayı veriyor, dolayısıyla tam beşte birlik kısmı hesaplamak için aşağıdaki formülü uygulamamız gerekiyor:

$K=x_i+d\cdot (x_{i+1}-x_i)$

İlk formülden elde edilen sayı 8,6’dır, yani ilk beşte birlik dilim sırasıyla 78 ve 79 olan sekizinci ve dokuzuncu veriler arasındadır. Dolayısıyla x _i 78, x _i+1 79 ve d elde edilen sayının ondalık kısmı yani 0,6’dır.

$K_1=78+0,6\cdot (79-78)=78,6$

Şimdi ikinci beşte birlik kısmı bulmak için aynı işlemi tekrar yapıyoruz. İlk önce konumunu hesaplıyoruz:

$\cfrac{2\cdot (42+1)}{5}=17,2$

Ancak formülden 17 ile 18 arasında bir ondalık sayı elde ederiz, böylece ikinci beşte birlik kısım, değerleri sıralı listenin sırasıyla 109 ve 112’sine karşılık gelen on yedinci ve on sekizinci konumlar arasında olacaktır. Bu nedenle, tam beşte birlik değeri belirlemek için süreçte ikinci formülü uyguluyoruz:

$K_2=109+0,2\cdot (112-109)=109,6$

Üçüncü beşte birlik kısmı elde etmek için yöntemi tekrarlıyoruz, önce konumunu belirliyoruz:

$\cfrac{3\cdot (42+1)}{5}=25,8$

Hesaplanan 25,8 sayısı, beşte birlik değerin, değerleri 134 ve 141 olan yirmi beşinci ve yirmi altıncı konumlar arasında olacağı anlamına gelir. Bu nedenle tam beşte birlik değerin hesaplanması şu şekildedir:

$K_3=134+0,8\cdot (141-134)=139,6$

Son olarak 4’üncü dilimin hesaplanması için aynı işlemi son kez tekrarlıyoruz. İlk önce konumunu buluyoruz:

$\cfrac{4\cdot (42+1)}{5}=34,4$

Bu nedenle dördüncü beşte birlik dilimin kesin değeri 34 ile 35 arasında olacaktır ve konumları 172 ve 179 numaralı verilere karşılık gelir. Bu nedenle dördüncü beşte birliğin hesaplanması şu şekildedir:

$K_4=172+0,4\cdot (179-172)=174,8$

Beşlik Hesap Makinesi

Beşte birlik dilimleri hesaplamak için aşağıdaki hesap makinesine istatistiksel veri kümesini girin. Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.

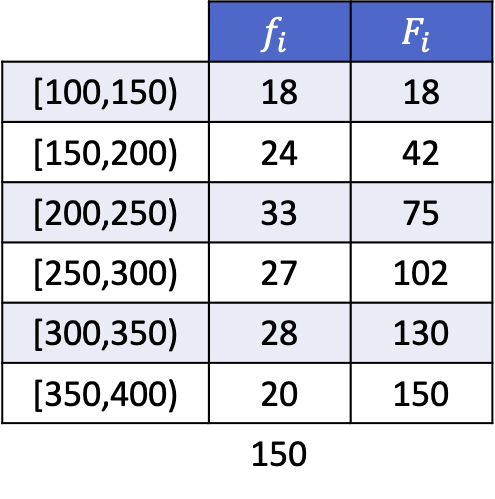
Gruplandırılmış verilerdeki beşte birlik dilimler

Veriler aralıklar halinde gruplandırıldığında beşte birlik dilimleri hesaplamak için öncelikle aşağıdaki formülü kullanarak aralığını veya sınıfını bulmanız gerekir:

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

Bu nedenle beşte birlik dilim, mutlak frekansı önceki ifadeyle elde edilen sayıdan hemen büyük olan aralıkta olacaktır.

Ve beşte birliğin ait olduğu aralığı bildiğimizde, beşte birliğin tam değerini bulmak için aşağıdaki formülü uygulamamız gerekir:

$K_k=L_i+ \cfrac{\displaystyle\frac{k\cdot (n+1)}{5}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3,4$

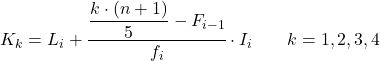
Altın:

L _i beşte birlik dilimin bulunduğu aralığın alt sınırıdır.
n , toplam gözlem sayısıdır.
F _i-1 önceki aralığın kümülatif mutlak frekansıdır.
f _i, beşte birlik dilimin bulunduğu aralığın mutlak frekansıdır.
I _i beşte birlik aralığın genişliğidir.

Bunun nasıl yapıldığını görebilirsiniz; burada, aralıklar halinde gruplandırılmış aşağıdaki veri serilerinin beşte birlik dilimlerinin hesaplanmasına ilişkin çözülmüş bir örnek verilmiştir:

Veriler gruplandırılmış olduğundan, beşte birlik dilimleri hesaplamak için aşağıdaki yöntemi kullanmamız gerekir: önce beşte birlik dilimin düştüğü aralığı belirleyin, ardından beşte birlik dilimin tam değerini bulun.

Bu nedenle, ilk beşte birlik dilimin bulunduğu aralığı bulmak için aşağıdaki formülü kullanırız:

$\cfrac{k\cdot (n+1)}{5}$

$\cfrac{1\cdot (150+1)}{5} =30,2 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [150,200)$

İlk yüzdelik dilim, kümülatif mutlak frekansı 30,2’den hemen büyük olan aralıkta olacaktır; bu durumda, kümülatif mutlak frekansı 42 olan aralık [150,200) olacaktır. Ve yüzdelik dilim aralığını bildiğimizde, denklemin ikinci formülünü uygularız. Kesin değerini belirlemek için süreç:

$K_k=L_i+ \cfrac{\displaystyle\frac{k\cdot (n+1)}{5}-F_{i-1}}{f_i}\cdot I_i$

$K_1=150+\cfrac{\displaystyle\frac{1\cdot (150+1)}{5}-18}{24}\cdot 50=175,42$

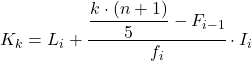
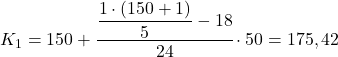
Şimdi ikinci beşte birlik kısmı elde etmek için aynı prosedürü tekrarlıyoruz, önce onun içinde bulunduğu aralığı hesaplıyoruz:

$\cfrac{2\cdot (150+1)}{5} =60,4 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [200,250)$

60,4’ün hemen üzerindeki kümülatif mutlak frekans 75’tir, dolayısıyla ikinci beşte birlik aralık [200 250] olur. Bu nedenle, tam beşte birlik değeri hesaplamak için karşılık gelen değerleri ikinci formülde yerine koyarız:

$K_2=200+\cfrac{\displaystyle\frac{2\cdot (150+1)}{5}-42}{33}\cdot 50=227,88$

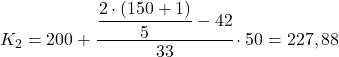
Beşte birlik 3’ü elde etmek için aynı işlemi üçüncü kez yapıyoruz. İlk önce beşte birliğin bulunduğu aralığı belirliyoruz:

$\cfrac{3\cdot (150+1)}{5} =90,6 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [250,300)$

Beşlik dilim [250,300) aralığındadır çünkü kümülatif mutlak frekansı (102) 90,6’nın hemen üzerindedir. Üçüncü beşte birlik dilimin kesin değerinin hesaplanması bu nedenle aşağıdaki gibidir:

$K_3=250+\cfrac{\displaystyle\frac{3\cdot (150+1)}{5}-75}{27}\cdot 50=278,89$

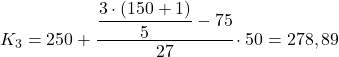
Sonunda dördüncü beşte birlik kısmı bulacağız. Her zaman olduğu gibi önce aralığını buluyoruz:

$\cfrac{4\cdot (150+1)}{5} =120,8 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [300,350)$

Mutlak frekansı 120,8’den hemen büyük olan aralık [300,350] olup değeri 130’dur. Dolayısıyla dördüncü beşte birlik dilimin tam değeri şu şekilde olacaktır:

$K_4=300+\cfrac{\displaystyle\frac{4\cdot (150+1)}{5}-102}{28}\cdot 50=333,57$

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Beşte birlikler nedir?

Beşte birlik dilimler nasıl hesaplanır

Beşte birlik dilimleri hesaplama örnekleri

örnek 1

Örnek 2

Beşlik Hesap Makinesi

Gruplandırılmış verilerdeki beşte birlik dilimler

yazar hakkında

Dr.benjamin anderson

Yorum ekle