İstatistikte beta düzeyi nedir? (tanım & #038; örnek)

İstatistikte, bir popülasyon parametresi hakkındaki bir hipotezin doğru olup olmadığını belirlemek için hipotez testini kullanırız.

Bir hipotez testi her zaman aşağıdaki iki hipoteze sahiptir:

Boş hipotez (H ₀ ): Örneklem verileri, popülasyon parametresine ilişkin baskın inançla tutarlıdır.

Alternatif Hipotez ( _HA ): Örnek veriler sıfır hipotezinde belirtilen hipotezin doğru olmadığını göstermektedir. Başka bir deyişle, rastgele olmayan bir neden verileri etkiler.

Ne zaman bir hipotez testi yapsak, her zaman dört olası sonuç vardır:

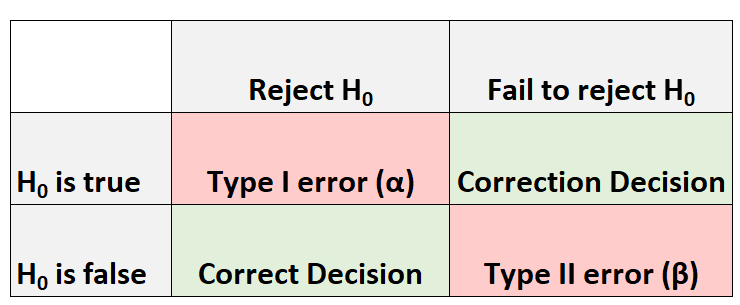
Yapabileceğimiz iki tür hata vardır:

• Tip I hatası: Gerçekten doğru olduğunda sıfır hipotezini reddederiz. Bu tür hatanın gerçekleşme olasılığı α ile gösterilir.
• Tip II hata: Gerçekten yanlış olan sıfır hipotezini reddedemeyiz. Bu tür hatanın gerçekleşme olasılığı β olarak belirtilir.

Alfa ve beta arasındaki ilişki

İdeal olarak araştırmacılar Tip I hata yapma olasılığının ve Tip II hata yapma olasılığının düşük olmasını isterler.

Ancak bu iki olasılık arasında bir uzlaşma söz konusudur. Alfa düzeyini düşürürsek, gerçekte doğru olan bir sıfır hipotezini reddetme olasılığımızı azaltabiliriz, ancak bu aslında beta düzeyini, yani yanlış olan sıfır hipotezini reddetmede başarısız olma olasılığımızı artırır.

Güç ve beta arasındaki ilişki

Bir hipotez testinin gücü , bir etki veya fark gerçekten mevcut olduğunda, bir etki veya farklılığın tespit edilme olasılığını ifade eder. Başka bir deyişle, yanlış bir sıfır hipotezinin doğru şekilde reddedilme olasılığıdır.

Aşağıdaki şekilde hesaplanır:

Güç = 1 – β

Genel olarak araştırmacılar bir testin gücünün yüksek olmasını isterler ki, eğer bir etki ya da farklılık varsa test bunu tespit edebilsin.

Yukarıdaki denklemden bir testin gücünü arttırmanın en iyi yolunun beta seviyesini düşürmek olduğunu görebiliriz. Beta düzeyini azaltmanın en iyi yolu genellikle örneklem boyutunu artırmaktır.

Aşağıdaki örnekler bir hipotez testinin beta düzeyinin nasıl hesaplanacağını gösterir ve örneklem boyutunu artırmanın neden beta düzeyini azaltabileceğini gösterir.

Örnek 1: Bir Hipotez Testi için Beta Hesaplama

Bir araştırmacının bir fabrikada üretilen aletlerin ortalama ağırlığının 500 onstan az olup olmadığını test etmek istediğini varsayalım. Ağırlıkların standart sapmasının 24 ons olduğunu biliyoruz ve araştırmacı 40 parçacıktan oluşan rastgele bir örnek toplamaya karar veriyor.

α = 0,05’te aşağıdaki hipotezi gerçekleştirecektir:

• H ₀ : u = 500
• _HA : μ < 500

Şimdi üretilen aletlerin ortalama ağırlığının aslında 490 ons olduğunu hayal edin. Başka bir deyişle sıfır hipotezinin reddedilmesi gerekir.

Beta düzeyini (boş hipotezin aslında reddedilmesi gerekirken reddedilmeme olasılığı) hesaplamak için aşağıdaki adımları kullanabiliriz:

Adım 1: Reddedilemez bölgeyi bulun.

Kritik Z değeri hesaplayıcısına göre α = 0,05’te sol kritik değer -1,645’tir .

Adım 2: Reddedemeyeceğimiz minimum numuneyi bulun.

Test istatistiği şu şekilde hesaplanır: z = ( x – μ) / (s/ √n )

Örnek ortalama için bu denklemi çözebiliriz:

• x = µ – z*(s/ √n )
• x = 500 – 1,645*(24/ √40 )
• x = 493.758

Adım 3: Minimum örnek ortalamasının gerçekten oluşma olasılığını belirleyin.

Bu olasılığı şu şekilde hesaplayabiliriz:

• P(Z ≥ (493,758 – 490) / (24/√ 40 ))
• P(Z ≥ 0,99)

Normal CDF hesaplayıcısına göre Z ≥ 0,99 olma olasılığı 0,1611’dir .

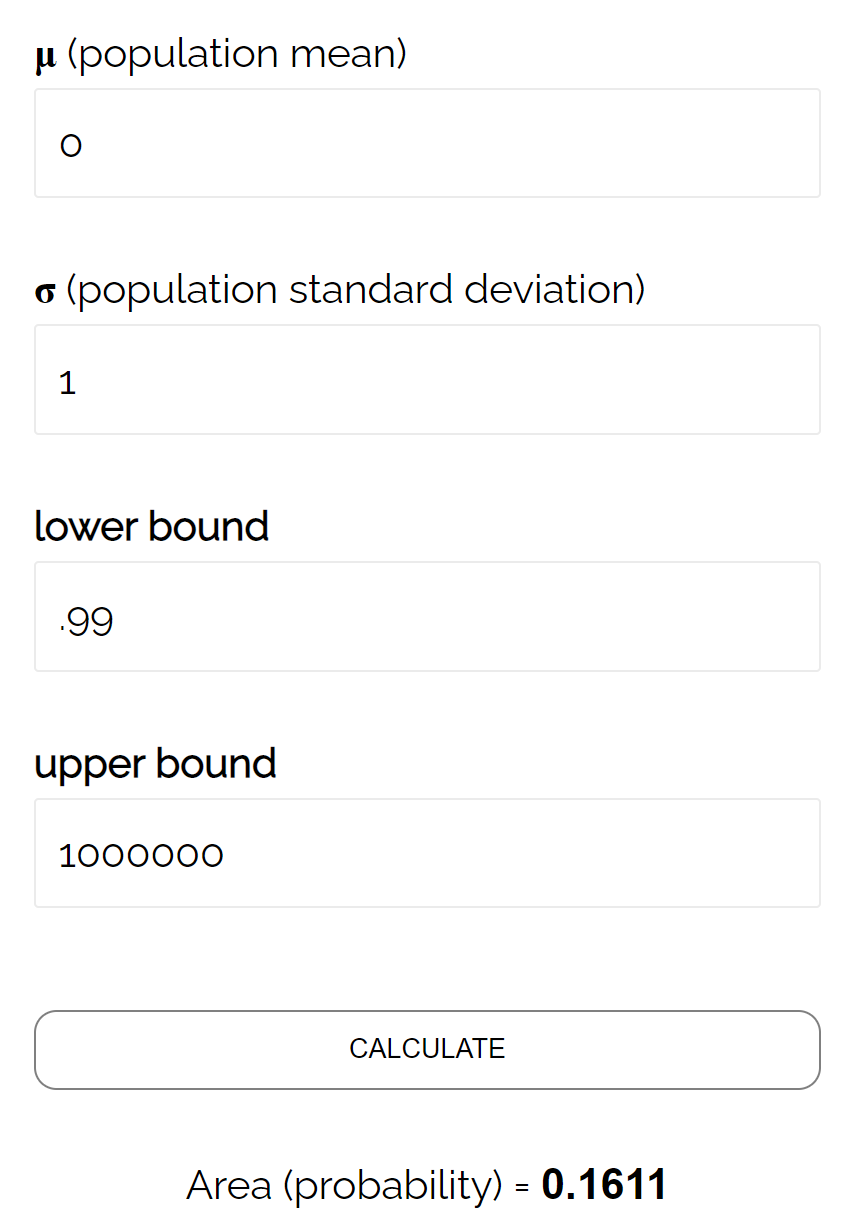
Dolayısıyla bu testin beta düzeyi β = 0,1611’dir. Bu, gerçek ortalamanın 490 ons olması durumunda farkın tespit edilememesi ihtimalinin %16,11 olduğu anlamına gelir.

Örnek 2: Daha Büyük Örneklem Boyutuna Sahip Bir Test için Beta Hesaplama

Şimdi araştırmacının tamamen aynı hipotez testini gerçekleştirdiğini, bunun yerine n = 100 parçacıktan oluşan bir örnek kullandığını varsayalım. Bu testin beta seviyesini hesaplamak için aynı üç adımı tekrarlayabiliriz:

Adım 1: Reddedilemez bölgeyi bulun.

Kritik Z değeri hesaplayıcısına göre α = 0,05’te sol kritik değer -1,645’tir .

Adım 2: Reddedemeyeceğimiz minimum numuneyi bulun.

Test istatistiği şu şekilde hesaplanır: z = ( x – μ) / (s/ √n )

Örnek ortalama için bu denklemi çözebiliriz:

• x = µ – z*(s/ √n )
• x = 500 – 1,645*(24/√ 100 )
• x = 496,05

Adım 3: Minimum örnek ortalamasının gerçekten oluşma olasılığını belirleyin.

Bu olasılığı şu şekilde hesaplayabiliriz:

• P(Z ≥ (496,05 – 490) / (24/√ 100 ))
• P(Z ≥ 2,52)

Normal CDF hesaplayıcısına göre Z ≥ 2,52 olma olasılığı 0,0059’dur.

Dolayısıyla bu testin beta düzeyi β = 0,0059’dur. Bu, gerçek ortalamanın 490 ons olması durumunda farkın tespit edilememesi ihtimalinin yalnızca %0,59 olduğu anlamına gelir.

Örneklem boyutunu 40’tan 100’e çıkararak araştırmacının beta seviyesini 0,1611’den 0,0059’a düşürebildiğini unutmayın.

Bonus: Bir testin beta düzeyini otomatik olarak hesaplamak için bu Tip II hata hesaplayıcıyı kullanın.

Ek kaynaklar

Hipotez Testine Giriş
Sıfır Hipotezi Nasıl Yazılır (5 Örnek)
P değerlerinin ve istatistiksel anlamlılığın açıklaması