Python'da binom dağılımı nasıl kullanılır

Binom dağılımı istatistikte en sık kullanılan dağılımlardan biridir. N sayıda binom deneyinde k başarı elde etme olasılığını açıklar.

Eğer bir X rastgele değişkeni binom dağılımını takip ediyorsa, X = k başarısının olasılığı aşağıdaki formülle bulunabilir:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Altın:

• n: deneme sayısı
• k: başarı sayısı
• p: belirli bir denemede başarı olasılığı
• _n C _k : n denemede k başarı elde etmenin yollarının sayısı

Bu eğitimde Python’da binom dağılımının nasıl kullanılacağı açıklanmaktadır.

Binom dağılımı nasıl oluşturulur?

Numpy kütüphanesinin random.binomial fonksiyonunu kullanarak binom dağılımını takip eden bir değerler dizisi oluşturabilirsiniz:

 from numpy import random

#generate an array of 10 values that follows a binomial distribution
random.binomial(n=10, p=.25, size=10)

array([5, 2, 1, 3, 3, 3, 2, 2, 1, 4])

Ortaya çıkan tablodaki her sayı, belirli bir denemede başarı olasılığının 0,25 olduğu 10 deneme boyunca karşılaşılan “başarı” sayısını temsil eder.

Binom dağılımını kullanarak olasılıkları hesaplama

Ayrıca scipy kütüphanesinin binom fonksiyonunu kullanarak binom olasılığıyla ilgili soruları da yanıtlayabilirsiniz.

Soru 1: Nathan serbest atış denemelerinin %60’ını yapıyor. Eğer 12 serbest atış yaparsa tam olarak 10 atış yapma olasılığı nedir?

 from scipy.stats import binom

#calculate binomial probability
binom.pmf(k= 10 , n= 12 , p= 0.6 )

0.0639

Nathan’ın tam olarak 10 serbest atış yapma olasılığı 0,0639’dur .

Soru 2: Marty adil bir yazı tura 5 kez atıyor. Paranın 2 veya daha az kez tura gelme olasılığı nedir?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 2 , n= 5 , p= 0.5 )

0.5

Paranın 2 veya daha az kez tura gelme olasılığı 0,5’tir .

Soru 3: Bireylerin %70’inin belirli bir yasayı desteklediğini biliyoruz. Eğer 10 kişi rastgele seçilirse, bunlardan 4 ila 6 tanesinin yasayı destekleme olasılığı nedir?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 6 , n= 10 , p= 0.7 ) - binom.cdf(k= 3 , n= 10 , p= 0.7 )

0.3398

Rastgele seçilen 4 ila 6 kişinin yasayı destekleme olasılığı 0,3398’dir .

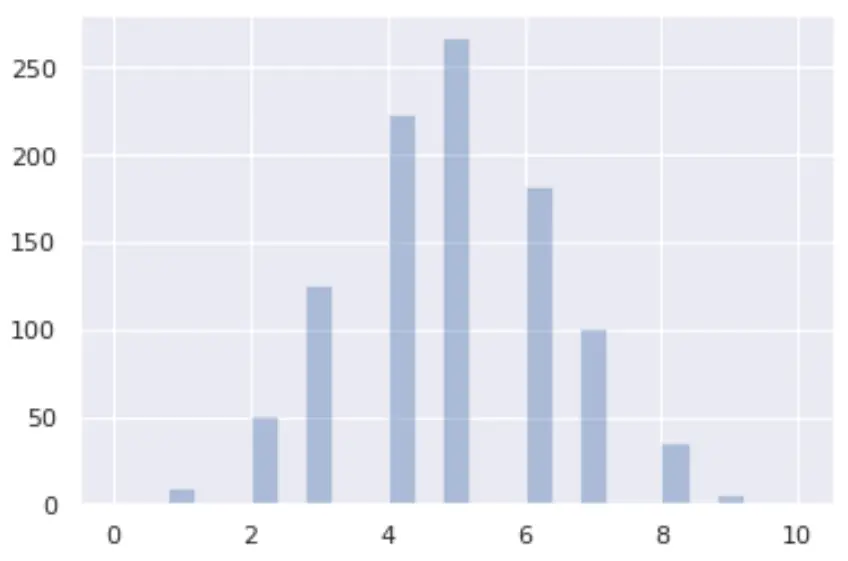
Binom dağılımı nasıl görselleştirilir?

Seaborn ve matplotlib kütüphanelerini kullanarak Python’da bir binom dağılımını görselleştirebilirsiniz:

 from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

x = random.binomial(n= 10 , p= 0.5 , size= 1000 )

sns.distplot(x, hist= True , kde= False )

plt.show()

Çay