Binom dağılımına giriş

Binom dağılımı istatistikte en popüler dağılımlardan biridir. Binom dağılımını anlamak için öncelikle binom deneylerini anlamak yardımcı olur.

Binom deneyleri

Binom deneyi aşağıdaki özelliklere sahip bir deneydir:

• Deney n tekrarlanan denemeden oluşur.
• Her denemenin yalnızca iki olası sonucu vardır.
• Başarı olasılığı p ile gösterilir, her deneme için aynıdır.
• Her test bağımsızdır.

Binom deneyinin en belirgin örneği yazı tura atmaktır. Örneğin, bir parayı 10 kez havaya attığımızı varsayalım. Bu bir binom deneyidir çünkü aşağıdaki dört özelliğe sahiptir:

• Deney n tekrarlanan denemeden oluşur – 10 deneme vardır.
• Her denemenin yalnızca iki olası sonucu vardır: yazı veya tura.
• Başarı olasılığı p ile gösterilir, her deneme için aynıdır. Başarıyı tura gelmek olarak tanımlarsak, başarı olasılığı her deneme için tam olarak 0,5’tir.
• Her deneme bağımsızdır – Bir yazı tura atışının sonucu, diğer yazı tura atışlarının sonucunu etkilemez.

Binom dağılımı

Binom dağılımı, n binom deneyinde k başarı elde etme olasılığını tanımlar.

Eğer bir X rastgele değişkeni binom dağılımını takip ediyorsa, X = k başarısının olasılığı aşağıdaki formülle bulunabilir:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Altın:

• n: deneme sayısı
• k: başarı sayısı
• p: belirli bir denemede başarı olasılığı
• _n C _k : n denemede k başarı elde etmenin yollarının sayısı

Örnek: Bir parayı 3 kez attığımızı varsayalım. Bu 3 atışta 0, 1, 2 ve 3 tura gelme olasılığını belirlemek için yukarıdaki formülü kullanabiliriz:

P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125

P(X=1) = ₃ C ₁ * 0,5 ¹ * (1-0,5) ^3-1 = 3 * 0,5 * (0,5) ² = 0,375

P(X=2) = ₃ C ₂ * 0,5 ² * (1-0,5) ^3-2 = 3 * 0,25 * (0,5) ¹ = 0,375

P(X=3) = ₃ C ₃ * 0,5 ³ * (1-0,5) ^3-3 = 1 * 0,125 * (0,5) ⁰ = 0,125

Not : Her _{örnekte nCk’yi} hesaplamak için bu birleşik hesap makinesini kullandık .

Bu olasılık dağılımını görselleştirmek için basit bir histogram oluşturabiliriz:

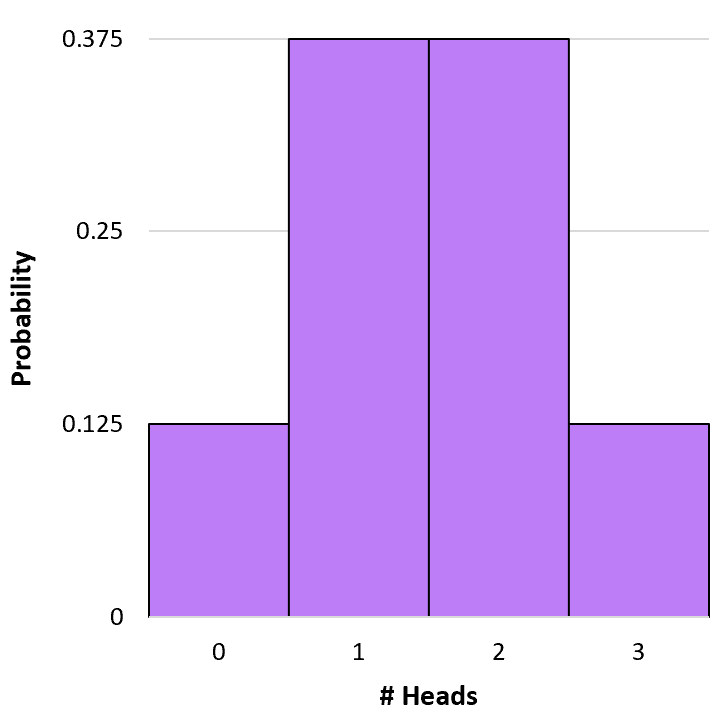
Kümülatif binom olasılıklarının hesaplanması

Yukarıdaki formülü kullanarak tek bir binom olasılığını (örneğin, 3 atıştan 1’inde bir paranın tura gelme olasılığı) hesaplamak kolaydır, ancak kümülatif binom olasılıklarını hesaplamak için bireysel olasılıkları toplamamız gerekir.

Örneğin, bir paranın 3 atıştan 1’inde veya daha azında tura gelme olasılığını bilmek istediğimizi varsayalım. Bu olasılığı hesaplamak için aşağıdaki formülü kullanırız:

P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .

Buna kümülatif olasılık denir çünkü birden fazla olasılığın eklenmesini içerir. Benzer bir formül kullanarak her sonuç için k veya daha az tura gelmenin kümülatif olasılığını hesaplayabiliriz:

P(X≤0) = P(X=0) = 0,125 .

P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .

P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0,125 + 0,375 + 0,375 = 0,875 .

P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0,125 + 0,375 + 0,375 + 0,125 = 1 .

Bu kümülatif olasılık dağılımını görselleştirmek için bir histogram oluşturabiliriz:

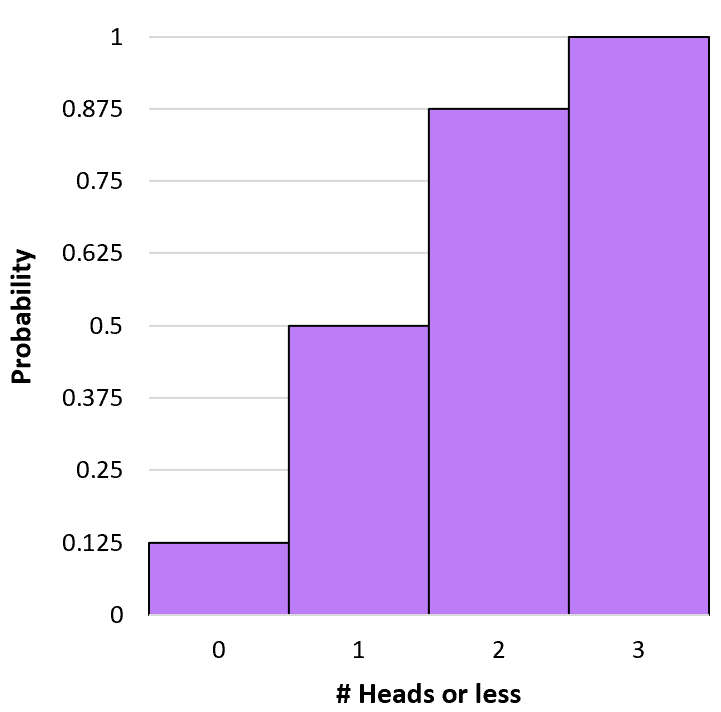
Binom Olasılık Hesaplayıcısı

Küçük sayılarla çalışırken (örneğin 3 yazı tura atıldığında), binom olasılıklarını elle hesaplamak mantıklıdır. Ancak daha büyük sayılarla çalıştığımızda (örneğin 100 beraberlik), olasılıkları elle hesaplamak zor olabilir. Bu durumlarda aşağıdaki gibi bir binom olasılık hesaplayıcısının kullanılması faydalı olabilir.

Örneğin, bir parayı n = 100 kez attığımızı, belirli bir denemede paranın tura gelme olasılığının p = 0,5 olduğunu ve k = 43 kez veya daha az tura gelme olasılığını bilmek istediğimizi varsayalım:

Sonucun nasıl yorumlanacağı aşağıda açıklanmıştır:

• Paranın tam olarak 43 kez tura gelme olasılığı 0,03007’dir .
• Paranın 43 defadan az tura gelme olasılığı 0,06661’dir .
• Paranın 43 veya daha az kez tura gelme olasılığı 0,09667’dir .
• Paranın 43 defadan fazla tura gelme olasılığı 0,90333’tür .
• Paranın 43 veya daha fazla kez tura gelme olasılığı 0,93339’dur .

Binom dağılımının özellikleri

Binom dağılımı aşağıdaki özelliklere sahiptir:

Dağılımın ortalaması μ = np’dir

Dağılımın varyansı: σ ² = np(1-p)

Dağılımın standart sapması σ = √ np(1-p)

Örnek: Bir parayı 3 kez havaya attığımızı varsayalım. P = madalyonun tura gelme olasılığı olsun.

Beklediğimiz ortalama yazı sayısı μ = np = 3*.5 = 1.5’tir .

Beklediğimiz kişi sayısı varyansı σ ² = np(1-p) = 3*.5*(1-.5) = 0.75’tir .

Binom Dağıtımı Uygulama Problemleri

Binom dağılımı bilginizi test etmek için aşağıdaki alıştırma problemlerini kullanın.

Sorun 1

Soru: Bob serbest atış denemelerinin %60’ını yapıyor. Eğer 12 serbest atış yaparsa tam olarak 10 atış yapma olasılığı nedir?

Cevap: Yukarıdaki p = 0,6, n = 12 ve k = 10 ile binom dağılım hesaplayıcısını kullanarak P(X=10) = 0,06385 olduğunu buluruz.

Sorun 2

Soru: Jessica 5 kez yazı tura atıyor. Paranın 2 veya daha az kez tura gelme olasılığı nedir?

Cevap: Yukarıdaki p = 0,5, n = 5 ve k = 2 olan binom dağılım hesaplayıcısını kullanarak P(X≤2) = 0,5 olduğunu buluruz.

Sorun 3

Soru: Belirli bir öğrencinin belirli bir üniversiteye kabul edilme olasılığı 0,2’dir. 10 öğrenci başvurursa 4’ten fazlasının kabul edilme olasılığı nedir?

Cevap: Yukarıdaki p = 0,2, n = 10 ve k = 4 olan binom dağılım hesaplayıcısını kullanarak P(X>4) = 0,03279’u buluruz.

Sorun 4

Soru: Bir parayı 12 kez atıyorsunuz. Ortaya çıkması beklenen ortalama kafa sayısı nedir?

Cevap: Binom dağılımının ortalamasının μ = np olarak hesaplandığını hatırlayın. Yani μ = 12*0,5 = 6 yazı .

Sorun 5

Soru: Mark denemelerinin %10’unda sayı atıyor. Belirli bir oyunda 5 deneme yaparsa, vurduğu home run sayısındaki fark nedir?

Yanıt: Binom dağılımının varyansının σ ² = np(1-p) şeklinde hesaplandığını hatırlayın. Böylece, ^σ2 = 6*.1*(1-.1) = 0.54 .

Ek kaynaklar

Aşağıdaki makaleler, binom dağılımını farklı istatistiksel yazılımlarda nasıl kullanacağınızı öğrenmenize yardımcı olabilir:

• Excel’de Binom Olasılıkları Nasıl Hesaplanır?
• TI-84 Hesap Makinesinde Binom Olasılıkları Nasıl Hesaplanır?
• R’de binom olasılıkları nasıl hesaplanır
• R’de binom dağılımı nasıl çizilir