Binom dağılımı

İle Dr.benjamin anderson Ağustos 3, 2023 Olasılık 0 Yorum

Bu makalede istatistikte binom dağılımının ne olduğu ve ne için kullanıldığı anlatılmaktadır. Bu nedenle binom dağılımının tanımını, binom dağılım örneklerini ve bu tür olasılık dağılımının özelliklerini bulacaksınız. Ek olarak, çevrimiçi bir hesap makinesiyle binom dağılımının herhangi bir olasılığını hesaplayabileceksiniz.

Binom dağılımı nedir?

Binom dağılımı, sabit bir başarı olasılığı ile bir dizi bağımsız, ikili deney gerçekleştirirken başarı sayısını sayan bir olasılık dağılımıdır.

Başka bir deyişle binom dağılımı, bir dizi Bernoulli denemesinin başarılı sonuçlarının sayısını tanımlayan bir dağılımdır.

Bernoulli testinin iki olası sonucu olan bir deney olduğunu unutmayın: “başarı” ve “başarısızlık”. Dolayısıyla “başarı” olasılığı p ise, “başarısızlık” olasılığı q=1-p’dir .

Genel olarak gerçekleştirilen deneylerin toplam sayısı n parametresi ile tanımlanırken, p her deneyin başarı olasılığıdır. Böylece, binom dağılımını takip eden bir rastgele değişken şu şekilde yazılır:

$X\sim\text{Bin}(n,p)$

Binom dağılımında aynı deneyin n kez tekrarlandığını ve deneylerin birbirinden bağımsız olduğunu, dolayısıyla her deneyin başarı olasılığının aynı olduğunu (p) unutmayın.

Binom dağılımı aynı zamanda binom dağılımı olarak da adlandırılabilir.

Binom Dağıtım Örnekleri

Binom dağılımının tanımını gördükten sonra, kavramı daha iyi anlamak için bu dağılım tipini takip eden çeşitli değişken örnekleri göreceğiz.

Bir paranın 25 kez atılması sırasında tura gelme sayısı.
Bir basketbolcunun aynı yerden potaya doğru 60 kez atış yaptığında yaptığı şut sayısı.
Bir zarı 30 kez atarak 6 sayısını elde etme sayısı.
Sınava giren toplam 50 öğrencinin geçme sayısı.
100 üründen oluşan bir numunedeki kusurlu birimlerin sayısı.

Binom dağılım formülü

x, n, p parametreleri verildiğinde, binom dağılımının olasılık fonksiyonu x çarpı p ^x çarpı (1-p) ^nx’teki n’nin kombinatoryal sayısı olarak tanımlanır.

Bu nedenle, binom dağılımının olasılığını hesaplamak için formül şöyledir:

👉Binom dağılımını takip eden bir değişkenin olasılığını hesaplamak için aşağıdaki hesaplayıcıyı kullanabilirsiniz.

Öte yandan, binom dağılımının kümülatif olasılığı, söz konusu başarı durumu sayısının olasılıkları ve önceki tüm olasılıkların eklenmesiyle hesaplanır. Dolayısıyla, binom dağılımının kümülatif olasılığını hesaplamak için formül şöyledir:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

Binom dağılımına ilişkin çözülmüş alıştırma

Bir parayı 10 kez atıyoruz, 6 kez tura gelme olasılığı nedir?

Bu problemdeki değişken binom dağılımını takip etmektedir çünkü tüm fırlatmalar birbirinden bağımsızdır ve aynı başarı olasılığına sahiptir.

Somut olarak başarı olasılığı %50’dir çünkü olası iki sonuçtan yalnızca biri başarı olarak kabul edilir.

$p=\cfrac{1}{2}=0,5$

Bu nedenle, bu alıştırmanın dağılımı, toplam 10 deneyden oluşan ve olasılığı 0,5 olan bir binomdur.

$X\sim\text{Bin}(10 ; 0,5)$

Dolayısıyla altı tura gelme olasılığını belirlemek için binom dağılım formülünü uygulamamız gerekir.

$\begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}$

Yani bir parayı on kez attığınızda tam olarak altı tura gelme olasılığı %20,51’dir.

Binom dağılımının özellikleri

Binom dağılımı aşağıdaki özelliklere sahiptir:

Binom dağılımı iki parametreyle tanımlanır: n , Bernoulli deneylerinin toplam sayısıdır ve p ise her Bernoulli deneyinin başarı olasılığıdır.

$\begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}$

Binom dağılımının ortalaması, toplam deney sayısının her bir deneyin başarı olasılığı ile çarpımına eşittir. Bu nedenle, bir binom dağılımının ortalamasını hesaplamak için n’yi p ile çarpmak gerekir.

$E[X]=n\cdot p$

Binom dağılımının varyansı, toplam deneme sayısının başarı olasılığı ve başarısızlık olasılığıyla çarpımına eşittir.

$Var(X)=n\cdot p\cdot (1-p)$

Binom dağılımının olasılık fonksiyonunun formülü aşağıdaki gibidir:

$\displaystyle P[X=x]&=\begin{pmatrix}n\\ x\end{pmatrix}p^x(1-p)^{n-x}$

Benzer şekilde, binom dağılımının kümülatif dağılım fonksiyonunun formülü şöyledir:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

Aynı olasılığa sahip iki bağımsız binom dağılımının toplamı, aynı olasılık değeri olan p ve n’nin iki dağılımın toplam deneme sayısının toplamı olduğu bir binom dağılımına eşdeğerdir.

$\begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}$

$\displaystyle P[Z=z]=\begin{pmatrix}n+m\\z\end{pmatrix}p^z(1-p)^{n+m-z}$

Bernoulli dağılımı, n=1 olan, yani sadece bir deneyin yapıldığı binom dağılımının özel bir durumudur.

$X\sim\text{Bin}(1,p) \quad \color{orange}\bm{\longrightarrow}\color{black}\quad X\sim\text{Bernoulli}(p)$

_Eğer _X 1 , _X ₂ ,…, X _k bağımsız rastgele değişkenlerse, öyle ki

$\displaystyle\sum_{i=1}^k X_i\sim \text{Bin}\left(\sum_{i=1}^k n_i,p\right)$

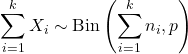
Binom Dağılımı Hesaplayıcı

Olasılığı hesaplamak için binom dağılımının p, n ve x parametrelerinin değerlerini aşağıdaki hesap makinesine girin. Hesaplamak istediğiniz olasılığı seçmeniz ve ondalık ayırıcı olarak noktayı kullanarak sayıları girmeniz gerekir, örneğin 0,1667.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil