R'de binom dağılımı nasıl çizilir

R’deki bir binom dağılımı için olasılık kütle fonksiyonunu çizmek için aşağıdaki fonksiyonları kullanabiliriz:

• olasılık kütle fonksiyonunu oluşturmak için dbinom(x, size, prob)
• arsa(x, y, type = ‘h’) grafiğin bir histogram olduğunu belirterek olasılık kütle fonksiyonunun grafiğini çizer (type=’h’)

Olasılık kütle fonksiyonunu çizmek için boyutu belirtmeniz yeterlidir.   (örneğin deneme sayısı) ve prob (örneğin belirli bir denemede başarı olasılığı) dbinom() işlevinde.

Örneğin, aşağıdaki kod, boyutu = 20 ve prob = 0,3 olan bir binom dağılımı için olasılık kütle fonksiyonunun nasıl çizileceğini gösterir:

 success <- 0:20

plot(success, dbinom(success, size=20, prob=.3), type='h')

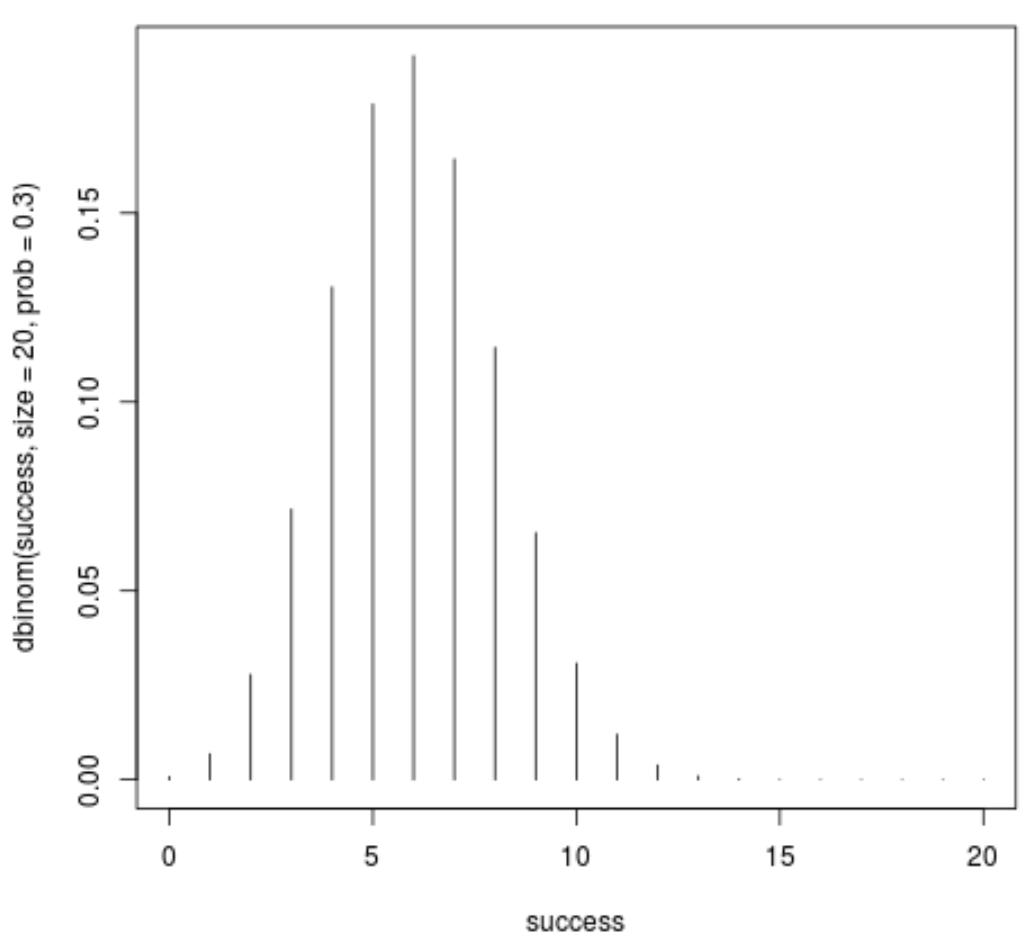
X ekseni başarı sayısını, y ekseni ise 20 denemede bu sayıda başarıyı elde etme olasılığını gösterir.

Grafiği estetik açıdan daha hoş hale getirmek için bir başlık ekleyebilir, eksen etiketlerini değiştirebilir ve çizgilerin genişliğini artırabiliriz:

 success <- 0:20

plot(success,dbinom(success,size=20,prob=.3),
     type='h',
     main='Binomial Distribution (n=20, p=0.3)',
     ylab='Probability',
     xlab ='# Successes',
     lwd=3)

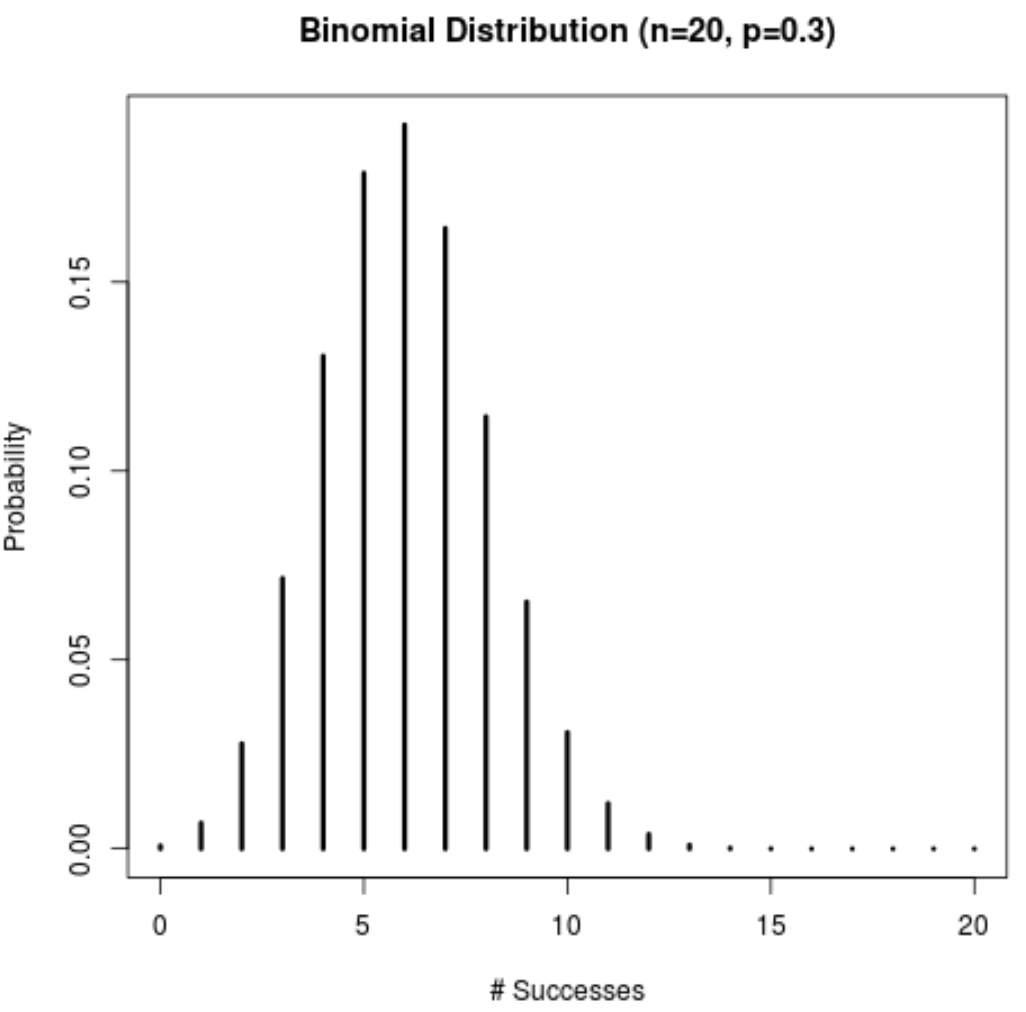
Grafikte görüntülenen her başarı sayısına ilişkin gerçek olasılıkları elde etmek için aşağıdaki kodu kullanabilirsiniz:

 #prevent R from displaying numbers in scientific notation
options(scipen=999) 

#define range of successes
success <- 0:20

#display probability of success for each number of trials
dbinom(success, size=20, prob=.3)

[1] 0.00079792266297612 0.00683933711122388 0.02784587252426865
[4] 0.07160367220526231 0.13042097437387065 0.17886305056987975
[7] 0.19163898275344257 0.16426198521723651 0.11439673970486122
[10] 0.06536956554563482 0.03081708090008504 0.01200665489613703
[13] 0.00385928193090119 0.00101783259716075 0.00021810698510587
[16] 0.00003738976887529 0.00000500755833151 0.00000050496386536
[19] 0.00000003606884753 0.00000000162716605 0.00000000003486784

Ek kaynaklar

Binom dağılımına giriş
Binom dağılımının şeklini anlama