Bir istatistiğin dayanıklı olması ne anlama gelir?

Bir istatistiğin uç değerlere duyarlı olmaması durumunda dayanıklı olduğu söylenir.

İşte esnek istatistiklere iki örnek:

• medyan
• çeyrekler arası aralık

İşte geçerli olmayan istatistik örnekleri:

• Ortalama
• Standart sapma
• Düzenli

Aşağıdaki örnek, dirençli ve dirençli olmayan istatistikler arasındaki farkı göstermektedir.

Örnek: Dirençli ve dirençli olmayan istatistikler

Aşağıdaki veri setine sahip olduğumuzu varsayalım:

Veri kümesi: 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29

Bir hesap makinesi veya istatistik yazılımı kullanarak, bu veri seti için aşağıdaki tutma istatistiklerinin değerini hesaplayabiliriz:

• Medyan: 13
• Çeyrekler arası aralık: 13,5

Bu veri kümesi için aşağıdaki esnek olmayan istatistiklerin değerini de hesaplayabiliriz:

• Ortalama: 13.54
• Standart sapma: 8,82
• Aralık: 27

Şimdi bu veri kümesine ekstrem bir aykırı değerin eklenip eklenmediğini düşünün:

Veri seti: 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29, 450

Bu veri kümesi için aşağıdaki esnek istatistiklerin değerini tekrar hesaplayabiliriz:

• Medyan: 14
• Çeyrekler arası aralık: 15,75

Bu veri kümesi için aşağıdaki esnek olmayan istatistiklerin değerini de hesaplayabiliriz:

• Ortalama: 49.92
• Standart sapma: 126,27
• Aralık: 448

Veri setine aşırı bir değer eklendiğinde direnç dışı istatistiklerin ne kadar değiştiğine dikkat edin:

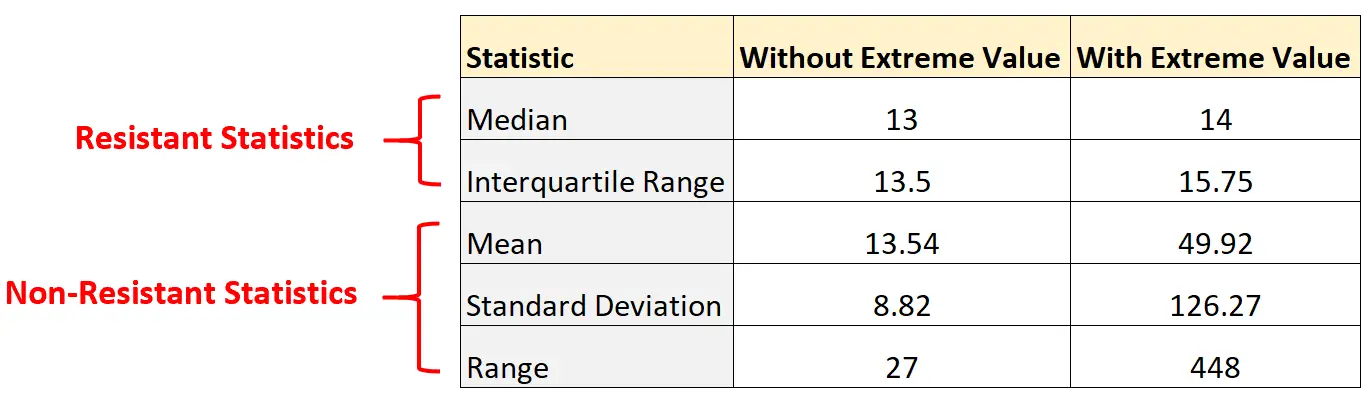
Tersine, direniş savaşçılarının istatistikleri pek değişmedi. Medyan ve çeyrekler arası aralık yalnızca çok az değişti.

Esnek istatistikler ne zaman kullanılmalı?

Bir veri setindeki değerlerin merkezini ve dağılımını ölçmek için en sık kullanılan istatistikler sırasıyla ortalama ve standart sapmadır.

Maalesef bu istatistiklerin her ikisi de uç değerlere duyarlıdır. Dolayısıyla, bir veri setinde aykırı değerler mevcutsa, ortalama ve standart sapma, bir veri setindeki değerlerin dağılımını doğru bir şekilde tanımlamayacaktır.

Bunun yerine, bu istatistiklerin her ikisi de sağlam olduğundan, aykırı değerler mevcutsa bir veri kümesindeki değerlerin merkezini ve dağılımını ölçmek için medyan ve çeyrekler arası aralığın kullanılması önerilir.

Ek kaynaklar

Aykırı değerler ortalamayı nasıl etkiler?
Ortalama ve medyan ne zaman kullanılmalı?
Çeyrekler arası aralık ve standart sapma ne zaman kullanılır?