R'de bray-curtis farklılığı nasıl hesaplanır

Bray-Curtis farklılığı, iki farklı bölge arasındaki farklılığı ölçmenin bir yoludur.

Ekoloji ve biyolojide genellikle iki alan arasındaki farkı, bu alanlarda bulunan türler açısından ölçmek için kullanılır.

Aşağıdaki şekilde hesaplanır:

BC _ij = 1 – (2*C _ij ) / (S _i + S _j )

Altın:

• C _ij : Her bir alanda bulunan türlere ait en düşük değerlerin toplamı.
• S _i : i sahasında sayılan toplam örnek sayısı
• S _j : j noktasında sayılan toplam örnek sayısı

Bray-Curtis farklılığı her zaman 0 ile 1 arasındadır; burada:

• 0 , iki sitenin hiçbir farklılığının olmadığını gösterir. Başka bir deyişle, her türden tam olarak aynı sayıda türü paylaşıyorlar.
• 1, iki sitenin tamamen farklı olduğunu gösterir. Yani aynı türden hiçbir türü paylaşmazlar.

Örneğin, bir botanikçinin dışarı çıkıp iki farklı bölgedeki beş farklı bitki türünün (A, B, C, D ve E) sayısını saydığını varsayalım.

Aşağıdaki tablo topladığı verileri özetlemektedir:

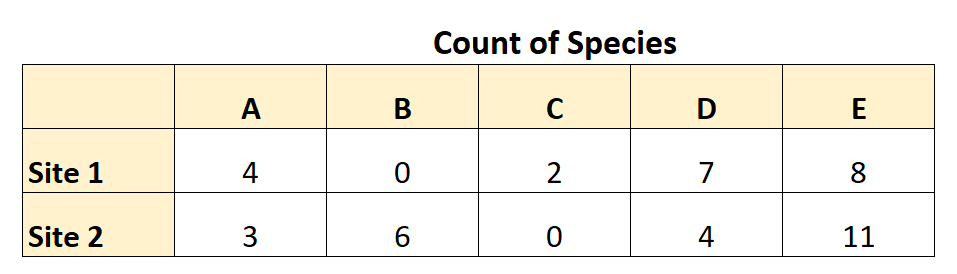
Bu verileri kullanarak Bray-Curtis farklılığını şu şekilde hesaplayabilir:

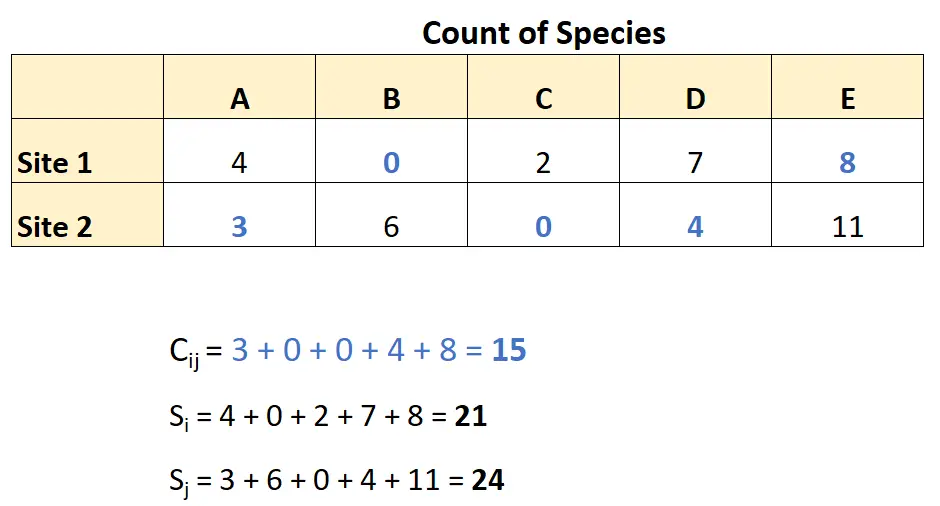
Bu sayıları Bray-Curtis farklılık formülüne entegre ederek şunu elde ederiz:

• BC _ij = 1 – (2*C _ij ) / (S _i + S _j )
• BC _ij = 1 – (2*15) / (21 + 24)
• BC _ij = 0,33

Bu iki bölge arasındaki Bray-Curtis farklılığı 0,33’tür .

Aşağıdaki örnek, R’deki Bray-Curtis farklılığının nasıl hesaplanacağını gösterir.

Örnek: R’de Bray-Curtis farklılığının hesaplanması

Öncelikle veri değerlerimizi tutmak için R’de aşağıdaki veri çerçevesini oluşturalım:

 #create data frame
df <- data. frame (A=c(4, 3),
                 B=c(0, 6),
                 C=c(2, 0),
                 D=c(7, 4),
                 E=c(8, 11))

#view data frame
df

  A B C D E
1 4 0 2 7 8
2 3 6 0 4 11

Veri çerçevesindeki iki satır arasındaki Bray-Curtis farklılığını hesaplamak için aşağıdaki kodu kullanabiliriz:

 #calculate Bray–Curtis dissimilarity
sum( apply (df, 2, function (x) abs ( max (x)- min (x)))) / sum ( rowSums (df))

[1] 0.3333333

Bray-Curtis’in farklı olduğu ortaya çıktı: 0,33 .

Bu, daha önce manuel olarak hesapladığımız değerle eşleşiyor.

Not : Bu formül yalnızca veri çerçevesindeki her satırın ayrı bir siteyi temsil etmesi durumunda işe yarar.

Ek kaynaklar

Aşağıdaki eğitimlerde R’deki diğer benzerlik ölçümlerinin nasıl hesaplanacağı açıklanmaktadır:

R’de Jaccard benzerliği nasıl hesaplanır
R’de kosinüs benzerliği nasıl hesaplanır