Çeyrekler
Bu yazıda çeyreklerin ne olduğunu açıklıyoruz. Her çeyreğin tanımını, bunların nasıl hesaplanacağını ve birkaç somut örneği bulacaksınız. Ayrıca gruplandırılmış veriler için çeyreklerin nasıl hesaplanacağını da gösteriyoruz. Ek olarak, çevrimiçi bir hesap makinesiyle herhangi bir veri kümesinin çeyreklerini hesaplayabileceksiniz.
Çeyrekler nedir?
İstatistikte çeyrekler, sıralı bir veri kümesini dört eşit parçaya bölen üç değerdir. Böylece birinci, ikinci ve üçüncü çeyrekler tüm istatistiksel verilerin sırasıyla %25, %50 ve %75’ini temsil etmektedir.
Çeyrekler büyük Q ve çeyrek endeksi ile temsil edilir, dolayısıyla ilk çeyrek Q 1 , ikinci çeyrek Q 2 ve üçüncü çeyrek Q 3’tür .
👉Herhangi bir veri setinin çeyreklerini hesaplamak için aşağıdaki hesap makinesini kullanabilirsiniz.
Çeyrek dilimlerin, beşte birlik dilimler, ondalık dilimler ve yüzdelik dilimlerle aynı şekilde merkezi olmayan konumun bir ölçüsü olduğuna dikkat edilmelidir. Bu nicelik türlerinin her birinin ne olduğunu bu web sayfasından kontrol edebilirsiniz.
ilk çeyrek
Çeyrek 1 olarak da adlandırılan ilk çeyrek , bir örnekteki istatistiksel verilerin %25’inden büyük olan değerdir. Başka bir deyişle, ilk çeyrek gözlemlenen verilerin %25’inden fazlasını temsil ediyor.
İlk çeyrek Q1 sembolü ile ifade edilir ve örnekteki en küçük veri değerlerini belirtmek için kullanılır.
ikinci çeyrek
İkinci çeyrek , aynı zamanda çeyrek 2 olarak da adlandırılır, bir örnekteki istatistiksel verilerin %50’sinden büyük olan değerdir. Dolayısıyla ikinci çeyrek, veri setini ikiye böler ve medyan ve beşinci ondalık dilime denk gelir.
İkinci çeyreğin sembolü Q2’dir .
üçüncü çeyrek
3. çeyrek olarak da adlandırılan üçüncü çeyrek , bir örneklemdeki istatistiksel verilerin %75’ini aşan değerdir. Başka bir deyişle üçüncü çeyrek, toplanan verilerin %75’inden fazlasını temsil ediyor.
Üçüncü çeyrek Q3 sembolü ile ifade edilir ve örnekteki en büyük değerleri temsil eder.
Çeyrekler nasıl hesaplanır
Bir istatistiksel veri kümesindeki çeyreklerin konumunu hesaplamak için, çeyrek sayısını toplam veri sayısının toplamının bir artısıyla çarpmanız ve sonucu dörde bölmeniz gerekir.
Dolayısıyla çeyreklerin formülü aşağıdaki gibidir:
![]()
Lütfen unutmayın: Bu formül bize çeyreğin değerini değil çeyreğin konumunu söyler. Çeyrek, formül tarafından elde edilen konumda bulunan veriler olacaktır.
Ancak bazen bu formülün sonucu bize ondalık bir sayı verecektir. Bu nedenle sonucun ondalık sayı olup olmamasına bağlı olarak iki durumu birbirinden ayırmamız gerekir:
- Formülün sonucu ondalık kısmı olmayan bir sayı ise çeyrek, yukarıdaki formülün sağladığı konumdaki verilerdir.
- Formül sonucu ondalık kısmı olan bir sayıysa çeyrek değeri aşağıdaki formül kullanılarak hesaplanır:
![]()
Burada x i ve x i+1, birinci formülle elde edilen sayının aralarında bulunduğu konumların sayılarıdır ve d , birinci formülle elde edilen sayının ondalık kısmıdır.
Belki çeyrekleri hesaplamak sizin için çok karmaşıktır çünkü dikkate alınması gereken pek çok şey vardır. Ancak bir sonraki bölümdeki iki örnekte bunun aslında ne kadar basit olduğunu göreceksiniz.
Not : Bilim camiasında çeyreklerin nasıl hesaplanacağı konusunda bir fikir birliği yoktur, dolayısıyla bunu biraz farklı açıklayan bir istatistik kitabı bulabilirsiniz.
Çeyrekleri hesaplama örnekleri
Çeyreklerin nasıl hesaplandığını tam olarak anlamak için aşağıda çözülmüş iki alıştırma bulacaksınız. İlkinde çeyrekler tam sayılardır ve ikincisinde çeyrekler ondalık sayılardır, böylece hangi iki durumu bulabileceğinizi görebilirsiniz.
örnek 1
- Aşağıdaki veri setinin üç çeyreğini hesaplayın:

Yukarıda gördüğümüz gibi çeyrekleri belirleme formülü şöyledir:
![]()
Bu durumda n , toplam gözlem sayısı 15’tir, bu nedenle ilk çeyreği bulmak için n’yi 15 ve k’yı 1 ile değiştirmeliyiz:
![]()
Bu nedenle, ilk çeyrek, sıralı değerler listesinin dördüncü konumundaki sayıdır; bu durumda bu sayı 39’dur.
Aynı şekilde, k katsayısını 2 ile değiştirerek ikinci çeyreği hesaplıyoruz:
![]()
Bu nedenle Çeyrek 2, sıralanmış listedeki 48 değerine karşılık gelen sekizinci sayıdır.
Son olarak üçüncü çeyreği hesaplamak için k =3 ile formülü son bir kez uyguluyoruz:
![]()
3. çeyrek onikinci konumdaki verilere, yani 60’a karşılık gelir.
Örnek 2
- Aşağıdaki veri serisinin üç çeyreğini bulun:

Bu ikinci örnekte 24 gözlemimiz var, dolayısıyla çeyrek formülünden elde edilen sayılar ondalık olacaktır.
İlk önce genel formülde k’yi 1’in yerine koyarak ilk çeyreğin konumunu hesaplıyoruz:
![]()
![]()
Ancak 6,25 ondalık sayısını elde ettik, yani ilk çeyrek sırasıyla 22 ve 25 olan altıncı ve yedinci veriler arasında yer alıyor. Bu nedenle, tam çeyreği hesaplamak için aşağıdaki formülü uygulamamız gerekir:
![]()
Bu durumda x i 22, x i+1 25 ve d elde edilen sayının ondalık kısmı yani 0,25’tir. Henüz:
![]()
Şimdi ikinci çeyreği bulmak için aynı işlemi yapıyoruz:
![]()
Yine formülden ondalık bir sayı elde ederiz, bu durumda 12,5 olur. Bu nedenle veri tablosundaki 49 ve 50’ye karşılık gelen on ikinci ve on üçüncü sayılar için aynı formülü kullanmalıyız:
![]()
Son olarak üçüncü çeyreği elde etmek için aynı işlemi tekrarlıyoruz:
![]()
Ancak 18,75 sayısı 18 ile 19 arasında olduğundan üçüncü çeyrek bu konumların değerleri (71 ve 73) arasında olacaktır. Daha doğrusu bu, aşağıdaki ifadeden elde ettiğimiz değer olacaktır:
![]()
çeyrek hesaplayıcı
Çeyrekleri hesaplamak için aşağıdaki hesap makinesine bir istatistiksel veri seti takın. Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.
Gruplandırılmış verilerdeki çeyrekler
Veriler aralıklar halinde gruplandırıldığında çeyrekleri hesaplamak için öncelikle aşağıdaki formülü kullanarak çeyreğin düştüğü aralığı veya bölmeyi bulmamız gerekir:
![]()
Bu nedenle çeyrek, mutlak kümülatif frekansı önceki ifadeyle elde edilen sayıdan hemen büyük olan aralıkta olacaktır.
Çeyreğin ait olduğu aralığı bildiğimizde, çeyreğin tam değerini bulmak için aşağıdaki formülü uygulamamız gerekir:
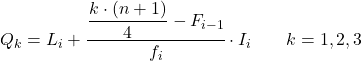
Altın:
- L i, çeyreğin bulunduğu aralığın alt sınırıdır.
- n , toplam gözlem sayısıdır.
- F i-1 önceki aralığın kümülatif mutlak frekansıdır.
- f i, çeyreğin bulunduğu aralığın mutlak frekansıdır.
- ben i çeyrek aralığının genişliğidir.
Örnek olarak burada bir dizi gruplandırılmış verideki çeyrekleri hesaplamaya yönelik bir alıştırma verilmiştir:

İlk çeyreği hesaplamak için öncelikle onun düştüğü aralığı belirlemelisiniz. Bunu yapmak için aşağıdaki formülü uyguluyoruz:
![]()
![]()
Yani ilk çeyrek, kümülatif mutlak frekansı 7,75’ten hemen büyük olan aralıkta olacaktır, bu durumda bu, kümülatif mutlak frekansı 15 olan aralıktır [50,60). Ve çeyrek aralığını bildiğimizde, ikinci süreç formülünü kullanırız. :
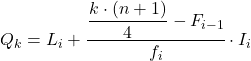
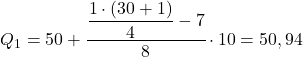
İkinci çeyreği elde etmek için aynı işlemi tekrar uyguluyoruz. İlk önce çeyreğin bulunduğu aralığı belirleriz:
![]()
Kümülatif mutlak frekansı 15,5’ten hemen büyük olan aralık [60,70] olup kümülatif mutlak frekansı 26’dır. Dolayısıyla ikinci çeyrek şu şekildedir:
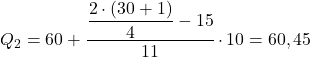
Ve son olarak üçüncü çeyreği bulmak için işlemi tekrarlıyoruz. İlk önce çeyreği içeren aralığı hesaplıyoruz:
![]()
23,25’in hemen üzerindeki kümülatif mutlak frekans 26’dır, dolayısıyla üçüncü çeyrek aralığı [60,70’tir. Bu nedenle bu aralığa sahip çeyreği hesaplamak için formülü uyguluyoruz:
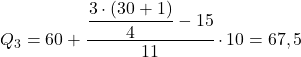
Çeyrekler ne için kullanılır?
Çeyrekler bir konum ölçüsüdür, dolayısıyla verilerin nasıl konumlandırıldığını bilmek için kullanılırlar. Başka bir deyişle, üç çeyreğin değerleri, örnekteki rastgele bir veri öğesinin çok büyük, çok küçük veya ortalama bir değer olup olmadığını bilmemizi sağlar.
Örnekten rastgele bir veri alırsak, bunu çeyreklerle karşılaştırarak değerinin yüksek mi yoksa düşük mü olduğunu anlayabiliriz. Rasgele verinin değeri ilk çeyrekten küçükse küçük bir değer olacaktır, ancak değeri üçüncü çeyrekten büyükse büyük bir değer olacaktır. Aynı şekilde söz konusu verinin değeri birinci ve üçüncü çeyrek arasında ise ara değerdir.
Öte yandan, çeyrekler aynı zamanda çeyrekler arası aralık (veya çeyrekler arası aralık) gibi diğer istatistiksel ölçümleri hesaplamak ve kutu ve bıyık grafiği (veya kutu grafiği) gibi diyagramlar oluşturmak için de kullanılır.