Çeyrekler arası aralık (iqr) aykırı değerlerden etkileniyor mu?

İstatistikte genellikle değerlerin bir dağılımda ne kadar geniş bir alana yayıldığını bilmek isteriz.

Yayılımı ölçmenin popüler bir yolu, bir veri kümesinin ilk dörtte biri ile üçüncü dörtte biri arasındaki fark olarak hesaplanan çeyrekler arası aralıktır . Çeyrekler basitçe bir veri kümesini dört eşit parçaya bölen değerlerdir.

Örnek: Çeyrekler arası aralığın hesaplanması

Aşağıdaki örnek, belirli bir veri kümesi için çeyrekler arası aralığın nasıl hesaplanacağını gösterir:

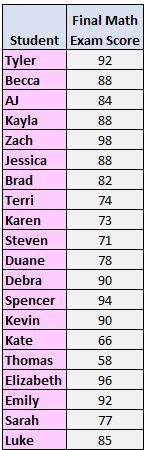
Adım 1: Değerleri en küçükten en büyüğe doğru sıralayın.

58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

2. Ortancayı bulun.

58, 66, 71, 73, 74, 77 , 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

Bu durumda medyan 85 ile 88 arasındadır.

3. Medyan veri setini ikiye böler. Alt yarının medyanı alt çeyrektir ve üst yarının medyanı üst çeyrektir:

58, 66, 71, 73, 74 , 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

4. Çeyrekler arası aralığı hesaplayın.

Bu durumda ilk çeyrek, veri setinin alt yarısındaki ortadaki iki değerin ortalamasıdır (75,5), üçüncü çeyrek ise set verilerinin üst yarısındaki orta iki değerin ortalamasıdır (91).

Yani çeyrekler arası aralık 91 – 75,5 = 15,5

Çeyrekler arası aralık aykırı değerlerden etkilenmez

İnsanların bir veri kümesinin “yayılımını” hesaplarken çeyrekler arası aralığı (IQR) kullanmayı tercih etmelerinin nedenlerinden biri, bunun aykırı değerlere karşı dayanıklı olmasıdır. IQR, veri değerlerinin ortadaki %50’lik aralığı olduğundan aşırı uç değerlerden etkilenmez.

Bunu göstermek için aşağıdaki veri kümesini göz önünde bulundurun:

[1, 4, 8, 11, 13, 17, 17, 20]

Bu veri kümesi için farklı yayılma ölçümleri şunlardır:

• Çeyrekler arası aralık: 11
• Aralık: 19
• Standart sapma: 6,26
• Fark: 39.23

Şimdi aynı veri setini düşünün, ancak aşırı uç değerler eklenmiş olarak:

[1, 4, 8, 11, 13, 17, 17, 20, 150 ]

Bu veri kümesi için farklı yayılma ölçümleri şunlardır:

• Çeyrekler arası aralık: 12,5
• Aralık: 149
• Standart sapma: 43,96
• Fark: 1.932,84

Çeyrekler arası aralığın 11’den 12,5’e kadar çok az değiştiğine dikkat edin. Bununla birlikte, diğer tüm dağılım ölçüleri önemli ölçüde değişir.

Bu, çeyrekler arası aralığın diğer dağılım ölçüleri gibi aykırı değerlerden etkilenmediğini göstermektedir. Bu nedenle herhangi bir dağılımda değerlerin ortadaki %50’lik dağılımını ölçmenin güvenilir bir yoludur.

Daha fazla okuma:

Dağılım ölçümleri
Çeyrekler Arası Aralık Hesaplayıcı