Chebyshev'in teoremi

İle Dr.benjamin anderson Ağustos 5, 2023 Olasılık 0 Yorum

Bu makale Chebyshev teoreminin ne olduğunu açıklamaktadır. Burada Chebyshev teoremi formülünü, çözülmüş bir alıştırmayı ve ayrıca çevrimiçi bir Chebyshev teoremi hesaplayıcısını bulacaksınız. Son olarak Chebyshev teoremi ile ampirik kural arasındaki farkı gösterir.

Chebyshev teoremi nedir?

Chebyshev eşitsizliği olarak da bilinen Chebyshev teoremi, rastgele bir değişkenin değerinin ortalamasından belirli bir mesafede bulunma olasılığını hesaplamak için kullanılan istatistiksel bir kuraldır.

Başka bir deyişle istatistikte Chebyshev teoremi, bir değerin güven aralığı dahilinde olma olasılığını belirlemek için kullanılır.

Ek olarak Chebyshev teoremi, büyük sayılar kanunu gibi diğer istatistiksel teoremleri kanıtlamak için de kullanılır.

Chebyshev teoremi ilk olarak Fransız Irénée-Jules Bienaymé tarafından formüle edilmiş olmasına rağmen, teorem 1867’de Rus Pafnuty Chebushev tarafından ortaya atıldığı için bu şekilde adlandırılmıştır.

Chebyshev teoreminin formülü

Chebyshev teoremi, bir değerin ortalamadan k standart sapmaya eşit olma olasılığının, bir eksi birin k kareye oranı kadar büyük veya ona eşit olduğunu söylüyor.

Bu nedenle Chebyshev teoreminin formülü aşağıdaki gibidir:

$\displaystyle P(\mu-k\sigma\leq X \leq \mu+k\sigma)\geq 1 -\frac{1}{k^2}$

Altın

$X$

rastgele değişkenin değeridir,

$\mu$

değişkenin aritmetik ortalaması ,

$\sigma$

standart sapması ve

$k$

olasılığın hesaplanacağı ortalamadan standart sapmaların sayısı.

Bu formülün yalnızca hesaplamanın yapıldığı standart sapma sayısı 1’den büyükse veya başka bir deyişle k 1’den büyükse kullanılabileceğini unutmayın.

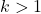$k>1″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”41″ style=”vertical-align: -2px;”></p> </p> <p> 👉 <u style=$ Olasılığı hesaplamak için aşağıdaki çevrimiçi Chebyshev Teoremi hesaplayıcısını kullanabilirsiniz.

Chebyshev teoreminin örneği

Chebyshev teoreminin tanımını ve formülünün ne olduğunu gördükten sonra, kavramı daha iyi anlamak için bu istatistiksel teoremin çözülmüş bir örneğini burada bulabilirsiniz.

Bir üniversitenin ders istatistiklerinde alınan notlar ortalaması 65, standart sapması 10 olan bir dağılımla tanımlanıyorsa, öğrencilerin yüzde kaçı 50 ile 80 arasında not almıştır?

Bu sorunu çözmek için Chebyshev teoreminin formülünü uygulamamız gerekiyor. Ancak öncelikle 50 ve 80 değerlerinin değişkenin ortalamasından kaç standart sapma olduğunu belirlememiz gerekiyor, bunun için aşağıdaki hesaplamayı yapmamız yeterli:

$k=\cfrac{\text{valor}-\text{media}}{\text{desviaci\'on t\'ipica}}$

$k=\cfrac{50-65}{10}=-1,5$

$k=\cfrac{80-65}{10}=1,5$

Dolayısıyla 50 ve 80 değerleri sırasıyla alt ve üst ortalamadan 1,5 standart sapmaya karşılık gelir. Bu nedenle Chebysheva teoreminin formülünü k=1,5 olarak kullanıyoruz:

$\displaystyle P(\mu-k\sigma\leq X \leq \mu+k\sigma)\leq 1 -\frac{1}{k^2}$

$\displaystyle P(\mu-1,5\sigma\leq X \leq \mu+1,5\sigma)\leq 1 -\frac{1}{1,5^2}$

$\displaystyle P(50\leq X \leq 80)\leq 0,5556$

Böylece öğrencilerin en az %55,56’sı 50 ile 80 arasında not aldı.

Chebyshev Teoremi Hesaplayıcısı

Söz konusu değerler ile ortalama (k) arasındaki standart sapma sayısını girin ve ardından “Hesapla”ya tıklayın. Hesap makinesi daha sonra güven aralığının minimum olasılığını döndürecektir.

Ondalık ayırıcı olarak noktayı kullanarak standart sapma sayısını girmelisiniz.

Chebyshev teoremi ve temel kural

İstatistikte birbiriyle yakından ilişkili iki kavram Chebyshev teoremi ve ampirik kuraldır, çünkü her ikisi de güven aralıklarının olasılığını hesaplamak için kullanılır.

Chebyshev teoremi ile ampirik kural arasındaki fark , Chebyshev teoreminin her türlü dağılımda kullanılabilmesi, ampirik kuralın ise yalnızca normal dağılım için geçerli olmasıdır.

Bu nedenle Chebyshev teoreminin kullanımı daha geniştir, ancak ampirik kural normal dağılım için daha kesin sonuçlar sağlar.

Temel kuralın tam olarak ne olduğunu görmek için burayı tıklayın:

➤ Bakınız: genel kural

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil