Chebyshev teoremi excel'de nasıl uygulanır?

Chebyshev teoremi, 1’den büyük herhangi bir k sayısı için, herhangi bir eğitimli dağılımdaki veri değerlerinin en az 1 – 1/k ^2’sinin ortalamadan k standart sapma dahilinde olduğunu belirtir.

Örneğin herhangi bir şekilli dağılım için dağılımdaki değerlerin en az 1 – 1/3 ² = %88,89’u ortalamanın 3 standart sapması dahilinde kalacaktır.

Bu eğitimde Chebyshev teoreminin Excel’de uygulanmasına ilişkin birkaç örnek gösterilmektedir.

Örnek 1: Ortalaması 50 ve standart sapması 10 olan bir veri seti için değerlerin yüzde kaçının 30 ile 70 arasında olacağını belirlemek için Chebyshev teoremini kullanın.

Öncelikle k’nin değerini belirleyin. Bunu ortalamadan 30 ile 70 arasında kaç standart sapma olduğunu belirleyerek yapabiliriz:

(30 – ortalama) / standart sapma = (30 – 50) / 10 = -20 / 10 = -2

(70 – ortalama) / standart sapma = (70 – 50) / 10 = 20 / 10 = 2

30 ve 70 değerleri sırasıyla ortalamanın altında ve üstünde 2 standart sapmadır. Yani k = 2 .

Daha sonra bu veri kümesi için ortalamanın 2 standart sapması dahilinde kalan değerlerin minimum yüzdesini bulmak için Excel’de aşağıdaki formülü kullanabiliriz:

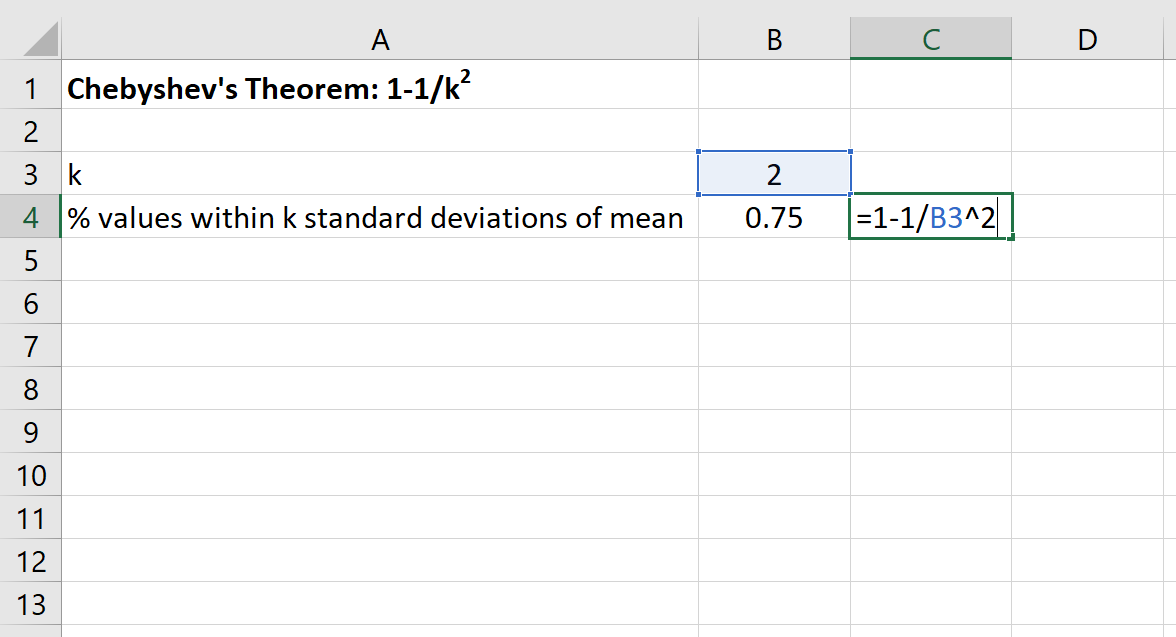
Bu veri seti için 30 ile 70 arasındaki değerlerin yüzdesi en az %75 olacaktır.

Örnek 2: Ortalaması 35 ve standart sapması 5 olan bir veri seti için değerlerin yüzde kaçının 20 ile 50 arasında olacağını belirlemek için Chebyshev teoremini kullanın.

Öncelikle k’nin değerini belirleyin. Bunu ortalamadan 20 ile 50 arasında kaç standart sapma olduğunu belirleyerek yapabiliriz:

(20 – ortalama) / standart sapma = (20 – 35) / 5 = -15 / 5 = -3

(50 – ortalama) / standart sapma = (50 – 35) / 5 = 15 / 5 = 3

20 ve 50 değerleri sırasıyla ortalamanın altında ve üstünde 3 standart sapmadır. Yani k = 3 .

Daha sonra bu veri kümesi için ortalamanın 3 standart sapması dahilinde kalan değerlerin minimum yüzdesini bulmak için Excel’de aşağıdaki formülü kullanabiliriz:

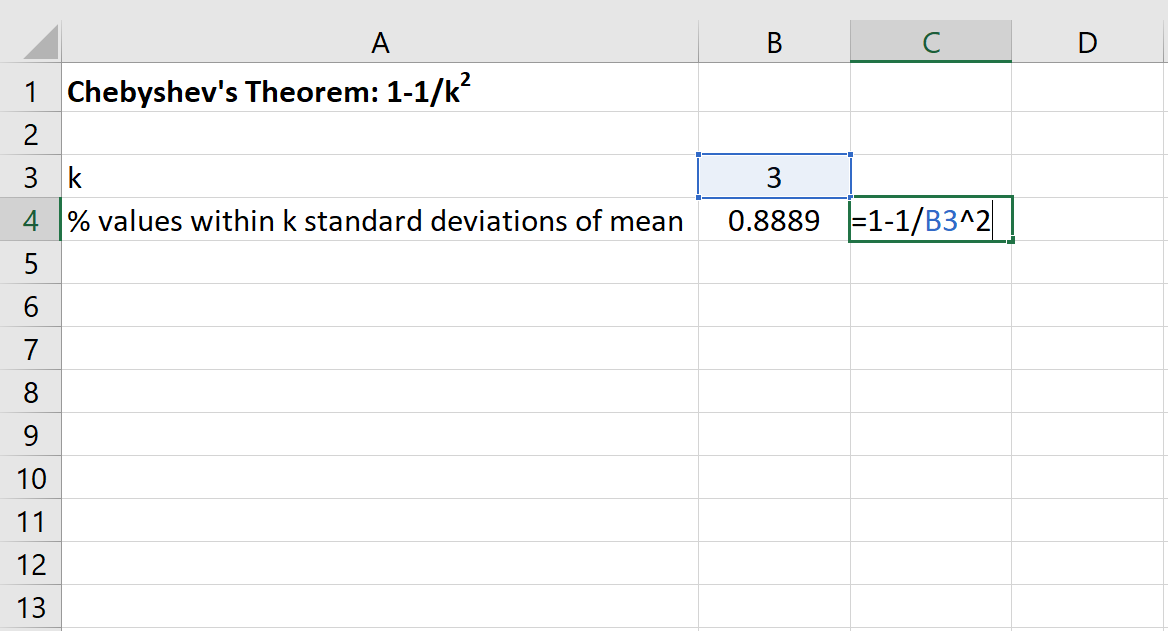
Bu veri seti için 20 ile 50 arasındaki değerlerin yüzdesi en az %88,89 olacaktır.

Örnek 3: Ortalaması 100 ve standart sapması 5 olan bir veri seti için değerlerin yüzde kaçının 80 ile 120 arasında olacağını belirlemek için Chebyshev teoremini kullanın.

Öncelikle k’nin değerini belirleyin. Bunu ortalamadan 80 ile 120 arasında kaç standart sapma olduğunu belirleyerek yapabiliriz:

(80 – ortalama) / standart sapma = (80 – 100) / 5 = -20 / 5 = -4

(120 – ortalama) / standart sapma = (120 – 100) / 5 = 20 / 5 = 4

80 ve 120 değerleri sırasıyla ortalamanın 4 standart sapma altında ve üstündedir. Yani k = 4 .

Daha sonra bu veri kümesi için ortalamanın 4 standart sapması dahilinde kalan değerlerin minimum yüzdesini bulmak için Excel’de aşağıdaki formülü kullanabiliriz:

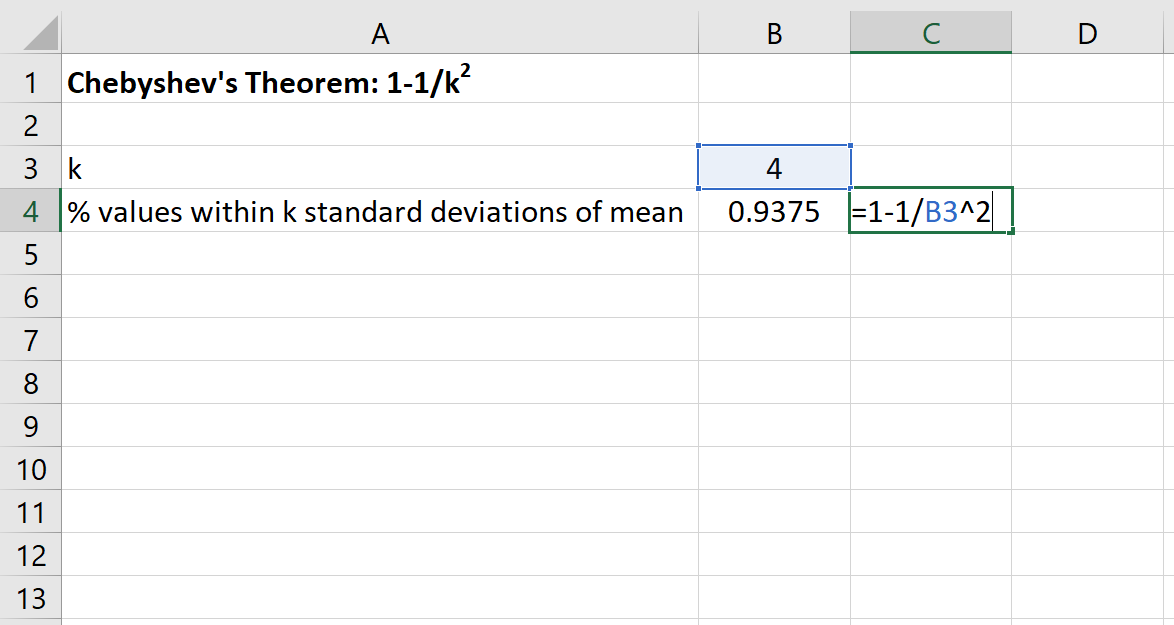
Bu veri seti için 80 ile 120 arasındaki değerlerin yüzdesi en az %93,75 olacaktır.