Cochran'ın q testi nedir? (tanım & #038; örnek)

Cochran’ın Q testi, her grupta aynı bireylerin yer aldığı üç veya daha fazla grupta “başarı” oranının eşit olup olmadığını belirlemek için kullanılan istatistiksel bir testtir.

Örneğin, üç farklı çalışma tekniği kullanıldığında bir testi geçen öğrencilerin oranının eşit olup olmadığını belirlemek için Cochran’ın Q testini kullanabiliriz.

Cochran’ın Q Testini Gerçekleştirme Adımları

Cochran’ın Q testi aşağıdaki boş ve alternatif hipotezleri kullanır:

Boş hipotez (H ₀ ): “Başarı” oranı tüm gruplarda aynıdır

Alternatif hipotez ( _HA ): Gruplardan en az birinde “başarı” oranı farklıdır

Test istatistiği şu şekilde hesaplanır:

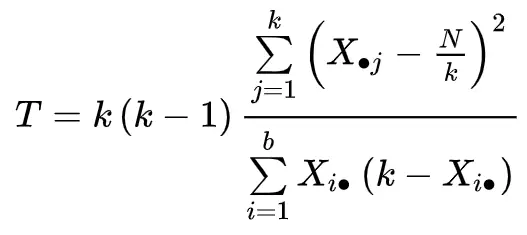
Altın:

• k: Tedavi sayısı (veya “grup”)
• Xj: ^j’inci muamele için sütunun toplamı
• b: Blok sayısı
• Xi. : ^i’inci blok için satırın toplamı
• N: Genel toplam

T testi istatistiği k-1 serbestlik derecesine sahip bir Ki-kare dağılımını takip eder.

Test istatistiğiyle ilişkili p değeri belirli bir anlamlılık düzeyinin altındaysa (örneğin, α = 0,05), sıfır hipotezini reddedebilir ve “başarı” oranının farklı olduğunu söylemek için yeterli kanıtımız olduğu sonucuna varabiliriz. gruplardan en az biri.

Örnek: Cochran’ın Q testi

Bir araştırmacının, üç farklı çalışma tekniğinin öğrenciler arasında farklı oranlarda başarı oranlarına yol açıp açmadığını bilmek istediğini varsayalım.

Bunu test etmek için, her biri üç farklı çalışma tekniği kullanarak eşit zorlukta bir sınava giren 20 öğrenciyi işe alıyor. Sonuçlar aşağıda gösterilmektedir:

Cochran’ın Q testini gerçekleştirmek için istatistiksel yazılım kullanabiliriz çünkü manuel olarak gerçekleştirmek sıkıcı olabilir.

Bu veri kümesini oluşturmak ve R istatistiksel programlama dilinde Cochran’ın Q testini gerçekleştirmek için kullanabileceğimiz kod:

 #load DescTools package
library (DescTools)

#create dataset
df <- data.frame(student= rep (1:20, each = 3 ),
                 technique= rep (c('A', 'B', 'C'), times= 20 ),
                 outcome=c(1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1,
                           1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1,
                           1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1,
                           1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1))

#perform Cochran's Q test
CochranQTest(outcome ~ technique| student, data=df)

	Cochran's Q test

data: outcome and technique and student
Q = 0.33333, df = 2, p-value = 0.8465

Test sonucundan aşağıdakileri gözlemleyebiliriz:

• Test istatistiği 0,333
• Karşılık gelen p değeri 0,8465’tir

Bu p değeri 0,05’ten küçük olmadığından sıfır hipotezini reddedemiyoruz.

Bu, öğrencilerin kullandığı çalışma tekniğinin farklı oranlarda başarı oranlarına yol açtığını söyleyecek yeterli kanıta sahip olmadığımız anlamına geliyor.