Çok terimli dağıtıma giriş

Çok terimli dağılım, her sonucun sabit bir gerçekleşme olasılığına sahip olduğu durumda, k farklı sonuç için belirli sayıda sayım elde etme olasılığını açıklar.

_{Eğer bir} rastgele değişken _{_} aşağıdaki formülle bulunabilirse:

Olasılık = n! * (p ₁ ^{x ₁} * p ₂ ^{x ₂} * … * p _k ^{x _k} ) / (x ₁ ! * x ₂ ! … * x _k !)

Altın:

• n: toplam olay sayısı
• x ₁ : sonuç 1’in oluşma sayısı
• p ₁ : belirli bir denemede sonuç 1’in ortaya çıkma olasılığı

Örneğin bir torbada 5 kırmızı, 3 yeşil ve 2 mavi bilye olduğunu varsayalım. Torbadan rastgele 5 bilyeyi yerine koyarak çekersek, tam olarak 2 kırmızı, 2 yeşil ve 1 mavi bilye elde etme olasılığı nedir?

Bu soruyu cevaplamak için çok terimli dağılımı aşağıdaki parametrelerle kullanabiliriz:

• sayı : 5
• x ₁ (# kırmızı bilyeler) = 2, x ₂ (# yeşil bilyeler) = 2, x ₃ (# mavi bilyeler) = 1
• p ₁ (kırmızı olasılık) = 0,5, p ₂ (yeşil olasılık) = 0,3, p ₃ (mavi olasılık) = 0,2

Bu sayıları formüle yerleştirdiğimizde olasılığın şöyle olduğunu buluruz:

Olasılık = 5! * (0,5 ² * 0,3 ² * 0,2 ¹ ) / (2! * 2! * 1!) = 0,135 .

Çok Terimli Dağıtım Uygulama Problemleri

Çok terimli dağılıma ilişkin bilginizi test etmek için aşağıdaki alıştırma problemlerini kullanın.

Not: Bu soruların cevaplarını hesaplamak için Multinomial Dağılım Hesaplayıcıyı kullanacağız.

Sorun 1

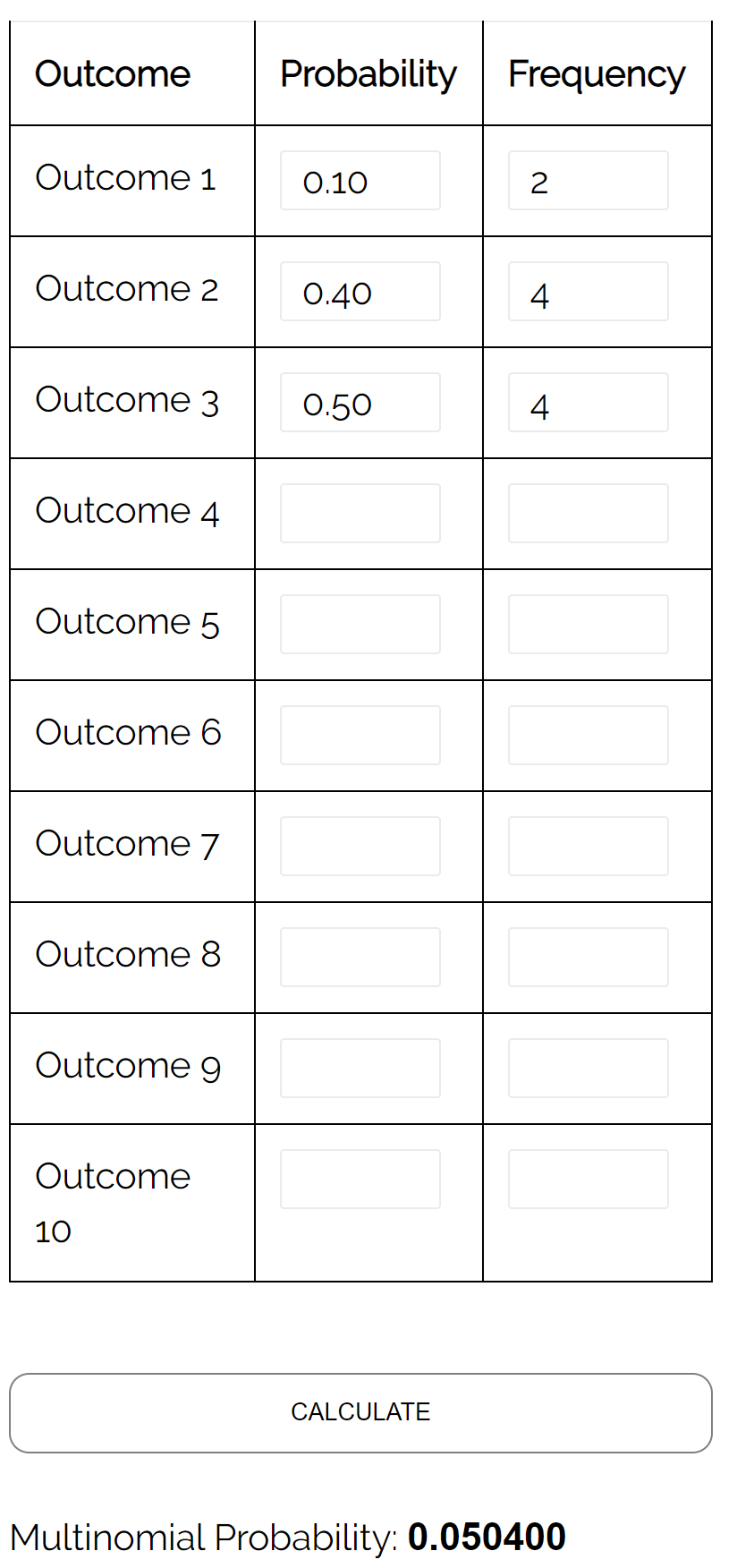
Soru: Üçlü belediye başkanlığı seçiminde A adayı yüzde 10, B adayı yüzde 40, C adayı yüzde 50 oy alıyor. 10 seçmenden oluşan rastgele bir örneklem seçersek, 2 kişinin A adayına, 4 kişinin B adayına ve 4 kişinin C adayına oy verme olasılığı nedir?

Cevap: Multinomial Dağılım Hesaplayıcısını aşağıdaki girdilerle kullanarak olasılığın 0,0504 olduğunu buluyoruz:

Sorun 2

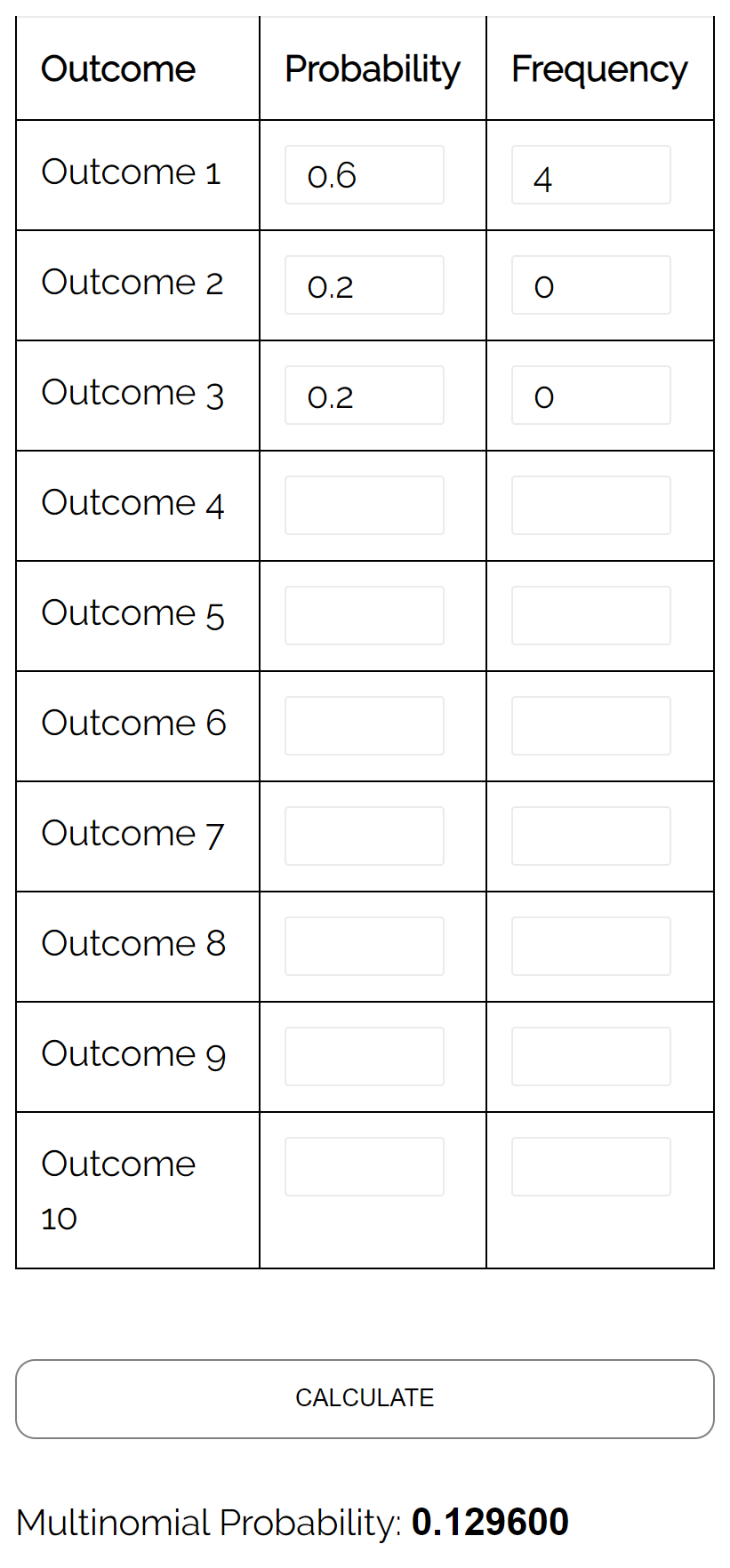
Soru: Bir vazoda 6 sarı bilye, 2 kırmızı bilye ve 2 pembe bilye bulunduğunu varsayalım. Torbadan rastgele 4 top seçersek ve yerine koyarsak, 4 topun da sarı olma olasılığı nedir?

Cevap: Multinomial Dağılım Hesaplayıcısını aşağıdaki girdilerle kullanarak olasılığın 0,1296 olduğunu buluyoruz:

Sorun 3

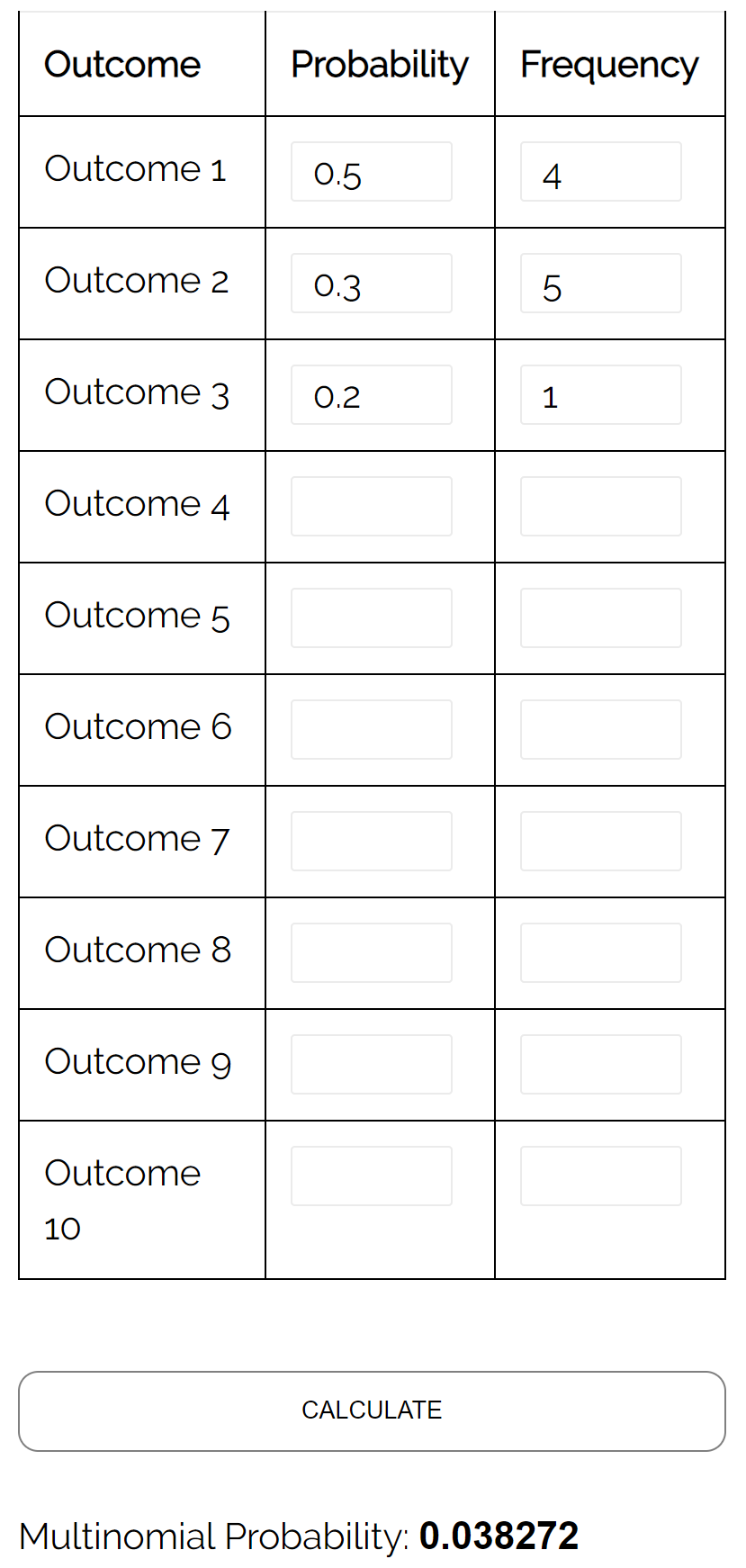
Soru: İki öğrencinin birbirlerine karşı satranç oynadığını varsayalım. A öğrencisinin belirli bir oyunu kazanma olasılığı 0,5, B öğrencisinin belirli bir oyunu kazanma olasılığı 0,3 ve belirli bir oyunda beraberlik olma olasılığı 0, 2’dir. Eğer 10 oyun oynarlarsa, A oyuncusunun 4 kez kazanması, B oyuncusunun 5 kez kazanması ve 1 kez berabere kalması olasılığı nedir?

Cevap: Multinomial Dağılım Hesaplayıcısını aşağıdaki girdilerle kullanarak olasılığın 0,038272 olduğunu buluyoruz:

Ek kaynaklar

Aşağıdaki eğitimler istatistikteki diğer yaygın dağılımlara bir giriş sağlar:

Normal dağılıma giriş
Binom dağılımına giriş
Poisson dağılımına giriş
Geometrik dağılıma giriş