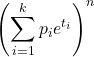Çok terimli dağılım

İle Dr.benjamin anderson Ağustos 4, 2023 Olasılık 0 Yorum

Bu makale istatistikte çok terimli dağılımın ne olduğunu açıklamaktadır. Böylece, çok terimli bir dağılımın tanımını, formülünün ne olduğunu, çözülmüş bir alıştırmayı ve bu tür olasılık dağılımının özelliklerinin neler olduğunu bulacaksınız. Ek olarak, çevrimiçi bir hesap makinesiyle çok terimli bir dağılımın olasılığını hesaplayabileceksiniz.

Çok terimli dağılım nedir?

Çok terimli dağılım (veya çok terimli dağılım ), birbirini dışlayan birkaç olayın birkaç denemeden sonra belirli sayıda meydana gelme olasılığını tanımlayan bir olasılık dağılımıdır.

Yani, rastgele bir deney üç veya daha fazla özel olayla sonuçlanabiliyorsa ve her olayın ayrı ayrı meydana gelme olasılığı biliniyorsa, çok terimli dağılım, birden fazla deney gerçekleştirildiğinde belirli sayıda olayın meydana gelme olasılığını hesaplamak için kullanılır. her zaman.

Dolayısıyla çok terimli dağılım, binom dağılımının bir genellemesidir.

Çok terimli dağılım formülü

Çok terimli bir dağılım olasılığını hesaplamak için, öncelikle toplam veri sayısının faktöriyeli ile her bir olayın meydana gelme sayısının faktöriyelleri arasındaki bölümü belirlemeniz gerekir ve sonuç, her olayın olasılığının çarpımı ile çarpılır. söz konusu olayın meydana gelme sayısına getirildi.

Başka bir deyişle multinomial dağılımın formülü şu şekildedir:

Altın:

$P$

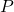
hesaplanan çok terimli dağılımın olasılığıdır.
$n$

gerçekleştirilen toplam test sayısıdır.
$x_i$

olayın meydana gelme sayısıdır

$i$

.
$p_i$

olayın meydana gelme olasılığı

$i$

.

👉 Multinomial dağılıma uyan bir değişkenin olasılığını hesaplamak için aşağıdaki hesaplayıcıyı kullanabilirsiniz.

Çok Terimli Dağılım Örneği

Çok terimli dağılım kavramını anlamayı tamamlamak için aşağıda çok terimli bir dağılımın olasılığını hesaplamaya ilişkin bir örneği çözdünüz.

Bir mağazada üç farklı ürün satılıyor. Bir müşteri bir satın alma işlemi gerçekleştirdiğinde bunun A ürünü, B ürünü veya C ürünü olma olasılığı sırasıyla %30, %15 ve %55’tir. Mağazada 8 adet satıldığında, 2 tanesinin A ürününden, 1 tanesinin B ürününden ve 5 tanesinin C ürününden olma olasılığını bulun.

Tanımlanan problem çok terimli bir dağılım tarafından yönetildiğinden, bu tür olasılık dağılımı için formülün uygulanması gereklidir:

$P=\cfrac{n!}{x_1!\cdot x_2!\cdot x_3!}\cdot p_1^{x_1}\cdot p_2^{x_2}\cdot p_3^{x_3}$

Böylece problemdeki verileri formülde yerine koyarız ve olasılık hesaplamasını yaparız:

$P=\cfrac{8!}{2!\cdot 1!\cdot 5!}\cdot 0,30^{2}\cdot 0,15^{1}\cdot 0,55^{5}=0,114$

Yani problem ifadesinin söylediği şeyin gerçekleşme olasılığı %11,4’tür.

Çok Terimli Dağıtım Hesaplayıcı

Her bir olayın gerçekleşme sayısını birinci kutuya, her olayın gerçekleşme olasılığını da aynı sırayla ikinci kutuya yazın. Daha sonra son boş alana yapılan toplam deneme sayısını girin.

Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.

Çok terimli dağılımın özellikleri

Çok terimli dağılım aşağıdaki özelliklere sahiptir:

Çok terimli bir dağılımda, n deneme çalıştırıldığında i olayının meydana gelme sayısının beklenen değeri, gerçekleştirilen toplam deneme sayısı ile olayın meydana gelme olasılığı çarpımına eşittir.

$E[x_i]=n\cdot p_i$

Çok terimli bir dağılımda i olayının varyansı aşağıdaki ifade kullanılarak hesaplanır:

$Var(x_i)=n\cdot p_i\cdot (1-p_i)$

Benzer şekilde, iki olay arasındaki kovaryans, toplam deneme sayısının her bir olayın olasılığı ile -1 ile çarpılmasının çarpımına eşdeğerdir:

$Cov(x_i,x_j)=-n\cdot p_i\cdot p_j\qquad i\neq j$

Çok terimli bir dağılım için moment üreten fonksiyon:

$\displaystyle \left(\sum_{i=1}^k p_ie^{t_i}\right) ^n$

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil