Excel'de çoklu doğrusal regresyon nasıl gerçekleştirilir

Çoklu doğrusal regresyon, iki veya daha fazla açıklayıcı değişken ile bir yanıt değişkeni arasındaki ilişkiyi anlamak için kullanabileceğimiz bir yöntemdir.

Bu eğitimde Excel’de çoklu doğrusal regresyonun nasıl gerçekleştirileceği açıklanmaktadır.

Not: Yalnızca bir açıklayıcı değişkeniniz varsa bunun yerine basit bir doğrusal regresyon gerçekleştirmelisiniz.

Örnek: Excel’de Çoklu Doğrusal Regresyon

Diyelim ki, ders çalışmak için harcanan saatlerin ve alınan hazırlık sınavlarının sayısının, bir öğrencinin belirli bir üniversiteye giriş sınavında aldığı notu etkileyip etkilemediğini bilmek istiyoruz.

Bu ilişkiyi araştırmak için, çalışılan saatleri ve alınan hazırlık sınavlarını açıklayıcı değişkenler olarak ve sınav sonuçlarını yanıt değişkeni olarak kullanarak çoklu doğrusal regresyon gerçekleştirebiliriz.

Çoklu doğrusal regresyon gerçekleştirmek için Excel’de aşağıdaki adımları tamamlayın.

Adım 1: Verileri girin.

20 öğrenci için çalışılan saat sayısı, girilen hazırlık sınavları ve alınan sınav sonuçları için aşağıdaki verileri girin:

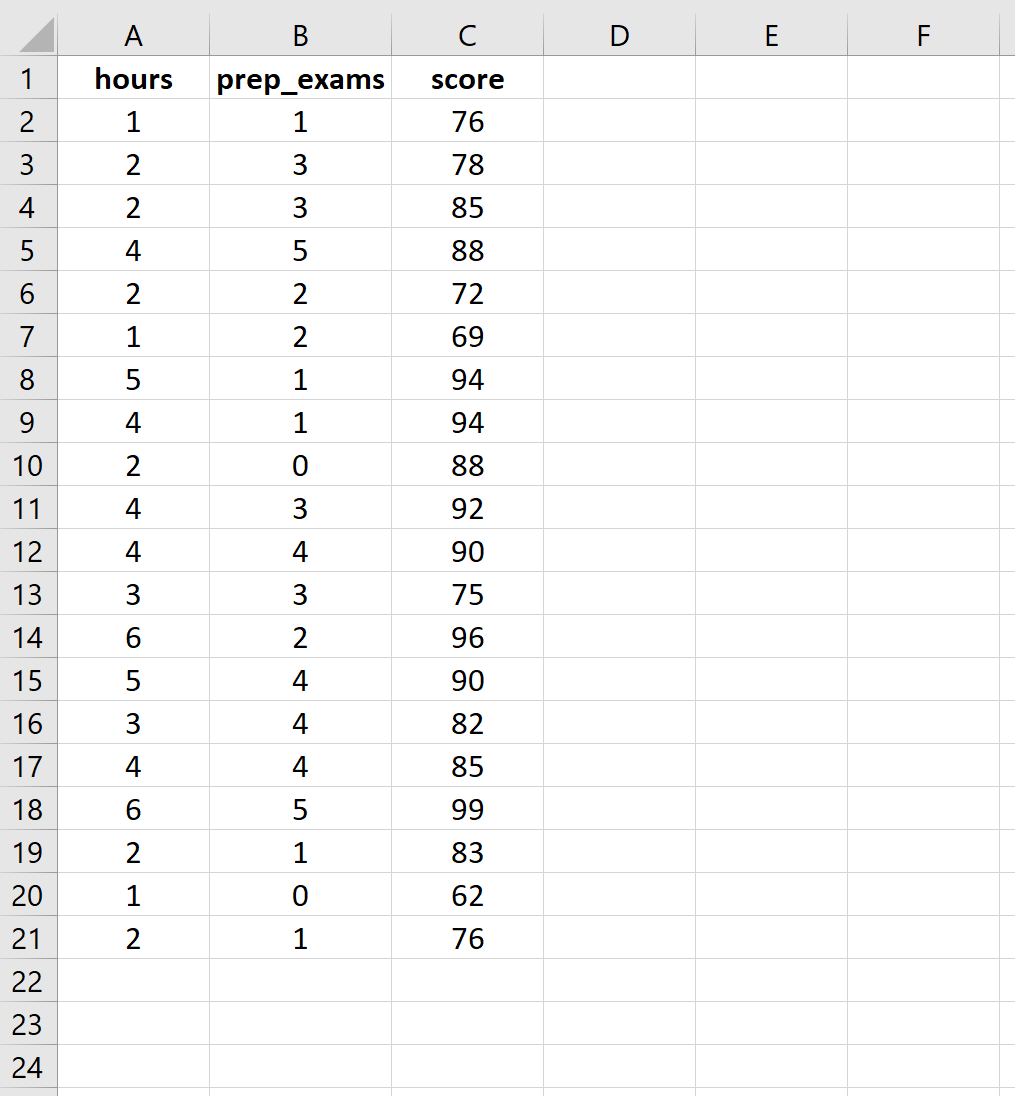
Adım 2: Çoklu doğrusal regresyon gerçekleştirin.

Excel’in üst şeridinde Veri sekmesine gidin ve Veri Analizi’ni tıklayın. Bu seçeneği görmüyorsanız, öncelikle ücretsiz Analysis ToolPak yazılımını yüklemelisiniz .

Veri Analizi’ne tıkladığınızda yeni bir pencere açılacaktır. Regresyon’u seçin ve Tamam’a tıklayın.

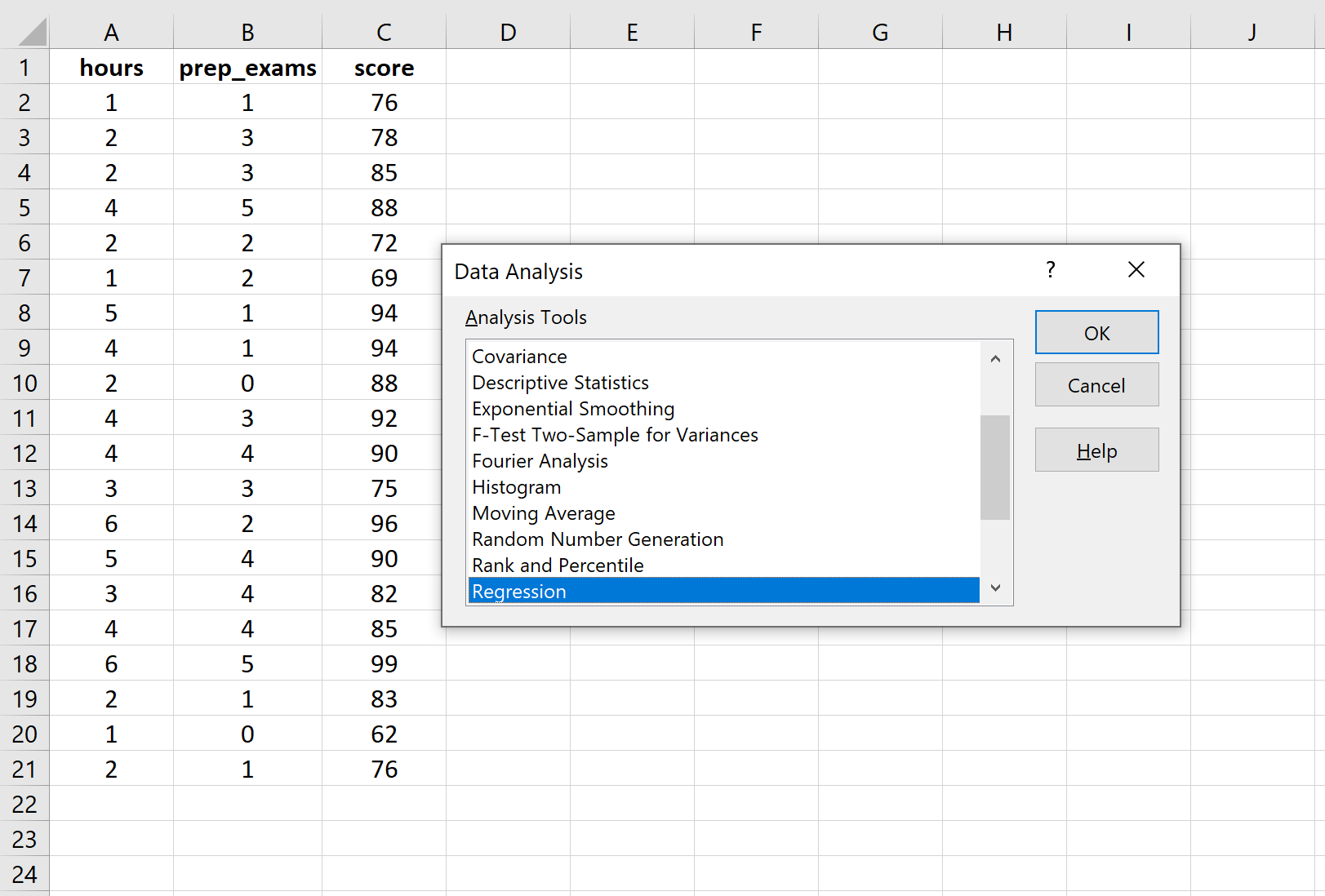
Giriş Y Aralığı için yanıt değişkenine ilişkin değerler dizisini doldurun. Giriş X Aralığı için iki açıklayıcı değişkenin değer dizisini doldurun. Excel’in değişken adlarını giriş aralıklarına dahil ettiğimizi bilmesini sağlamak için Etiketler’in yanındaki kutuyu işaretleyin. Çıkış Aralığı için regresyon çıktısının görünmesini istediğiniz hücreyi seçin. Daha sonra Tamam’ı tıklayın.

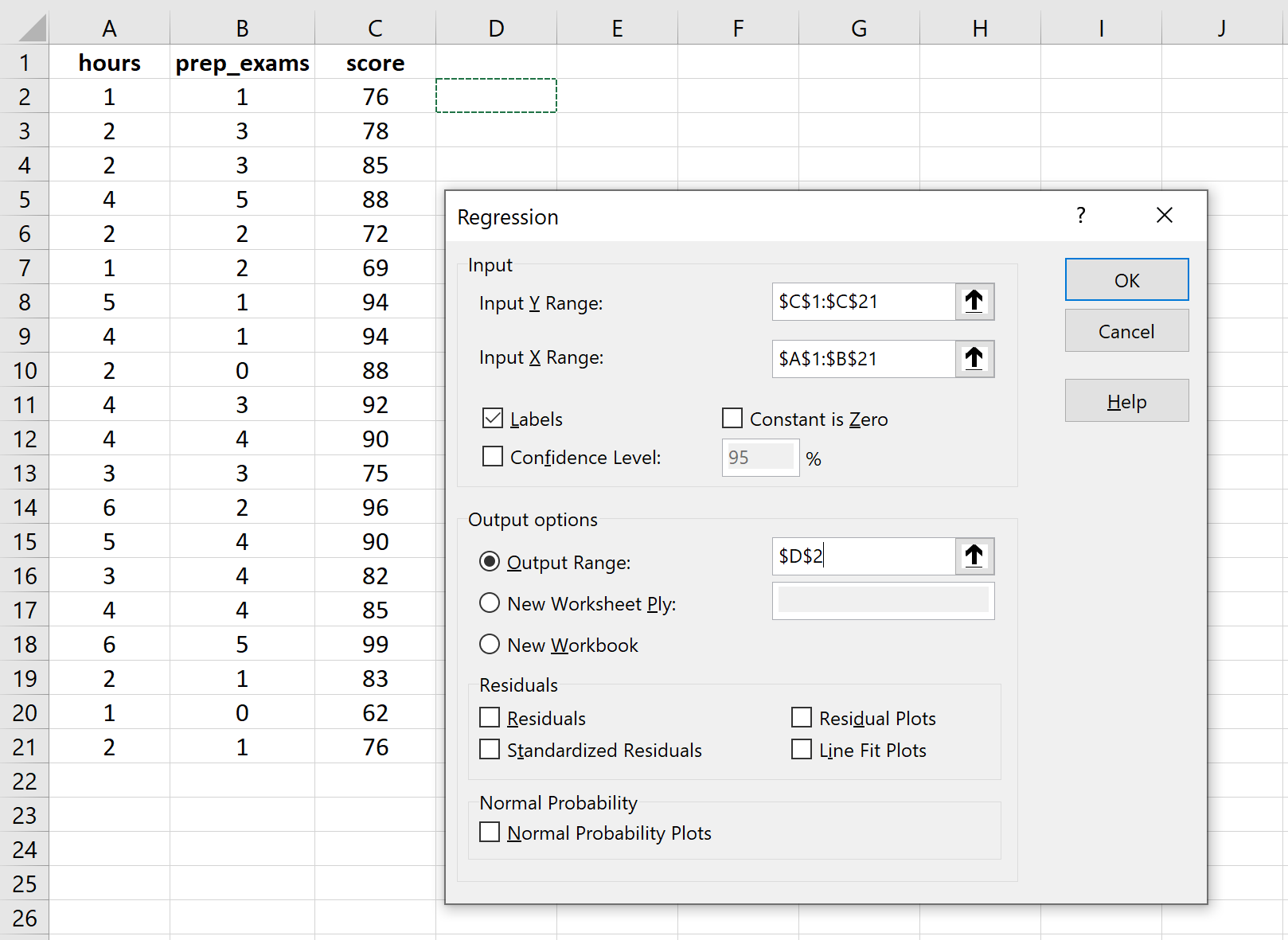
Aşağıdaki çıktı otomatik olarak görünecektir:

Adım 3: Sonucu yorumlayın.

Sonuçtaki en alakalı sayıları nasıl yorumlayacağınız aşağıda açıklanmıştır:

R Kare: 0,734 . Buna belirleme katsayısı denir. Açıklayıcı değişkenler tarafından açıklanabilen yanıt değişkeninin varyansının oranıdır. Bu örnekte sınav puanlarındaki farklılığın %73,4’ü çalışılan saat ve girilen hazırlık sınavı sayısıyla açıklanmaktadır.

Standart hata: 5,366 . Bu, gözlemlenen değerler ile regresyon çizgisi arasındaki ortalama mesafedir. Bu örnekte gözlemlenen değerler regresyon doğrusundan ortalama 5.366 birim sapmaktadır.

F: 23:46 Bu, regresyon modeli için regresyon MS/artık MS olarak hesaplanan genel F istatistiğidir.

Anlamı F: 0,0000 . Bu, genel F istatistiğiyle ilişkili p değeridir. Bu bize regresyon modelinin bir bütün olarak istatistiksel olarak anlamlı olup olmadığını söyler. Başka bir deyişle, bize iki açıklayıcı değişkenin birleşiminin yanıt değişkeni ile istatistiksel olarak anlamlı bir ilişkiye sahip olup olmadığını söyler. Bu durumda p değeri 0,05’ten küçüktür; bu durum, açıklayıcı değişkenlerin , çalışılan saatlerin ve girilen hazırlık sınavlarının birleşiminin sınav sonucuyla istatistiksel olarak anlamlı bir ilişkiye sahip olduğunu gösterir.

P değerleri. Bireysel p değerleri bize her açıklayıcı değişkenin istatistiksel olarak anlamlı olup olmadığını söyler. Çalışılan saatlerin istatistiksel olarak anlamlı olduğunu (p = 0,00), alınan hazırlık sınavlarının (p = 0,52) α = 0,05’te istatistiksel olarak anlamlı olmadığını görebiliriz. Geçmiş hazırlık sınavlarının istatistiksel olarak anlamlı olmaması nedeniyle onları modelden çıkarmaya karar verebiliriz.

Katsayılar: Her bir açıklayıcı değişkenin katsayıları, diğer açıklayıcı değişkenin sabit kaldığı varsayılarak, bize yanıt değişkeninde beklenen ortalama değişimi söyler. Örneğin, alınan deneme sınavlarının sabit kaldığı varsayılarak, ders çalışmak için harcanan her ek saat için ortalama sınav puanının 5,56 artması beklenir.

Buna başka bir açıdan da bakabiliriz: Öğrenci A ve Öğrenci B aynı sayıda hazırlık sınavına girerse ancak Öğrenci A bir saat daha uzun çalışırsa, Öğrenci A, Öğrenci B’den 5,56 puan daha yüksek puan almalıdır.

Kesişme katsayısını, ders saati çalışmayan ve hazırlık sınavına girmeyen bir öğrenci için beklenen sınav puanının 67,67 olduğu şeklinde yorumluyoruz.

Tahmini regresyon denklemi: Aşağıdaki tahmini regresyon denklemini oluşturmak için model çıktısındaki katsayıları kullanabiliriz:

sınav puanı = 67,67 + 5,56*(saat) – 0,60*(hazırlık sınavları)

Bu tahmini regresyon denklemini, bir öğrencinin çalışma saati ve girdiği deneme sınavlarının sayısına bağlı olarak beklenen sınav puanını hesaplamak için kullanabiliriz. Örneğin üç saat çalışıp hazırlık sınavına giren bir öğrencinin notunun 83,75 olması gerekir:

sınav puanı = 67,67 + 5,56*(3) – 0,60*(1) = 83,75

Geçmiş hazırlık sınavlarının istatistiksel olarak anlamlı olmaması (p=0,52) nedeniyle modelin geneline herhangi bir iyileştirme sağlamaması nedeniyle bunları kaldırmaya karar verebileceğimizi unutmayın. Bu durumda açıklayıcı değişken olarak yalnızca çalışılan saatleri kullanarak basit bir doğrusal regresyon gerçekleştirebiliriz.

Bu basit doğrusal regresyon analizinin sonuçlarını burada bulabilirsiniz.

Ek kaynaklar

Çoklu doğrusal regresyon gerçekleştirdikten sonra aşağıdakiler de dahil olmak üzere çeşitli varsayımları kontrol etmek isteyebilirsiniz:

1. VIF kullanarak çoklu bağlantının test edilmesi .

2. Breusch-Pagan testi kullanarak değişen varyansları test edin .

3. QQ grafiğini kullanarak normalliği test edin .